Momento Angular
El momento angular es una magnitud física que describe el estado de rotación de un cuerpo respecto a un punto o a un eje. $$ \vec{L} = \vec{r} \times \vec{p} = \vec{r} \times (m \vec{v}) $$ Donde:
- $\vec{r}$ = vector de posición con respecto al punto o eje de rotación elegido
- $\vec{p} = m \vec{v}$ = la cantidad de movimiento lineal, es decir, la masa $m$ del cuerpo multiplicada por su velocidad $ \vec{v} $
El producto vectorial $ \vec{r} \times \vec{p} $ da lugar a un vector perpendicular al plano definido por $\vec{r}$ y $\vec{v}$.
¿De qué depende el momento angular?
El momento angular está determinado por:
- la posición $ \vec{r} $ del cuerpo con respecto al punto de referencia $ O $
- su cantidad de movimiento lineal $ \vec{p} = m \vec{v} $
- la orientación del movimiento en relación con el vector de posición
Por ejemplo, en un movimiento circular no uniforme, un cuerpo describe una trayectoria circular con una velocidad tangencial que varía en el tiempo.
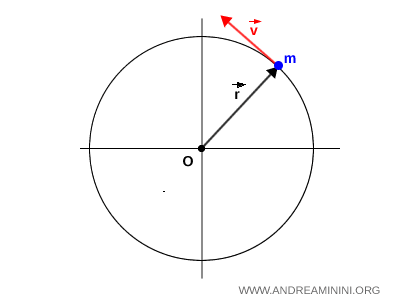
En este caso, la distancia $ r $ entre el cuerpo y el centro de rotación $ O $ permanece constante. Si la masa $ m $ del cuerpo también es fija, el momento angular resulta directamente proporcional a la velocidad tangencial $ \vec{v} $.
Nota. Incluso un cuerpo en movimiento rectilíneo puede poseer momento angular, siempre que su trayectoria no pase por el punto de referencia $ O $. En tal caso, el vector de posición $\vec{r}$ respecto a $ O $ sigue variando con el tiempo.
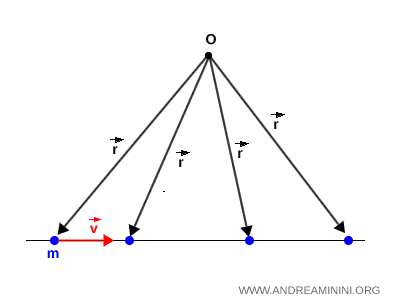
En cambio, si el movimiento rectilíneo pasa exactamente por $ O $, el momento angular se mantiene nulo en todo instante.
La magnitud del momento angular depende del ángulo $ \theta $ entre $ \vec{r} $ y $ \vec{v} $:
$$ L = mrv \cdot \sin \theta $$
Este valor puede variar entre dos extremos:
- Cuando $ \theta = 90^\circ $, el momento angular alcanza su valor máximo $ L = mrv $, ya que $ \vec{r} $ y $ \vec{v} $ son perpendiculares.
- Cuando $ \theta = 0^\circ $ o $ \theta = 180^\circ $, el momento angular se anula $ L=0 $, porque $ \vec{r} $ y $ \vec{v} $ son paralelos.
En líneas generales, el momento angular depende de la masa del cuerpo, de la parte de su posición que es perpendicular al eje de rotación, de su velocidad tangencial y del sistema de referencia que se elija para describir el movimiento.
También es importante tener en cuenta que el momento angular puede cambiar si varía la posición del cuerpo respecto al punto $ O $. Por este motivo, no se trata de una propiedad intrínseca del objeto, sino de una magnitud ligada a cómo y desde dónde se observa el sistema.
Un ejemplo práctico
Imaginemos a un atleta preparándose para el lanzamiento de martillo.
El martillo tiene una masa $m = 7{,}26\,\text{kg}$ y está unido a un cable de longitud $r = 1{,}20\,\text{m}$.
Mientras el atleta gira, el martillo describe un círculo horizontal alrededor del punto de agarre, que actúa como centro de rotación. Durante esta fase, el atleta aumenta de forma progresiva la velocidad tangencial del martillo.
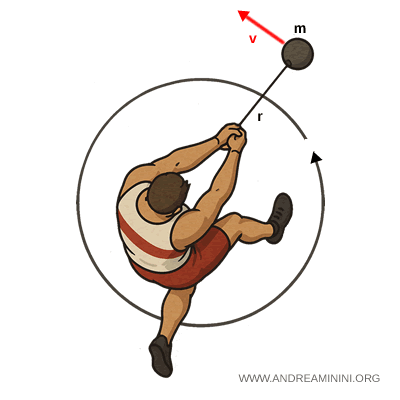
En el instante del lanzamiento, si la velocidad tangencial es $v = 28{,}0\,\text{m/s}$, el momento angular respecto al centro de rotación se obtiene como:
$$ L = m r v $$
Sustituyendo los valores:
$$ L = (7{,}26\,\text{kg}) \cdot (1{,}20\,\text{m}) \cdot (28{,}0\,\text{m/s}) $$
$$ L \approx 243{,}94\,\text{kg·m}^2/\text{s} $$
Por tanto, en el momento de la suelta el martillo posee un momento angular de $ L \approx 243{,}94\,\text{kg·m}^2/\text{s} $.
Este resultado depende de tres factores clave:
- La masa del martillo: cuanto mayor sea, mayor será $L$.
- El radio: cuanto más largo sea el brazo de palanca, mayor será $L$.
- La velocidad tangencial: es el factor decisivo, ya que es el que el atleta controla directamente durante el lanzamiento.
Si, por ejemplo, el atleta soltara el martillo a la mitad de la velocidad, $v = 14{,}0\,\text{m/s}$, el momento angular se reduciría a:
$$ L = 7{,}26 \cdot 1{,}20 \cdot 14{,}0 = 121{,}968 \approx 121{,}97\,\text{kg·m}^2/\text{s} $$
Esto implica que sería necesaria menos fuerza para frenar o modificar el movimiento de rotación respecto al punto de apoyo.
Nota. En el lanzamiento de martillo, tanto la masa $ m $ como el radio $ r $ son constantes. En esas condiciones, el momento angular es directamente proporcional a la velocidad tangencial $ v $. Dicho de otro modo: cuanto más rápido gire el martillo, más difícil será detenerlo. Ahora bien, un análisis más detallado debería considerar también las variaciones del radio efectivo derivadas de los movimientos del atleta y de la extensión de los brazos, que modifican $ r $ y, en consecuencia, el momento angular.
Ley de Conservación del Momento Angular
Si sobre un sistema no actúan torques externos, su momento angular total permanece constante.
Este principio está en la base de una amplísima gama de fenómenos físicos.
Por ejemplo, explica por qué un patinador gira más rápido al recoger los brazos o por qué satélites y planetas mantienen órbitas estables.
En definitiva, el momento angular depende de la masa del cuerpo, de la componente perpendicular de su posición respecto al eje de rotación, de su velocidad tangencial y del sistema de referencia adoptado.
Momento angular de la Tierra
La dinámica de la Tierra en el espacio está marcada por dos formas de momento angular. Cada una explica, desde una perspectiva diferente, por qué nuestro planeta mantiene una rotación regular y una órbita estable alrededor del Sol.
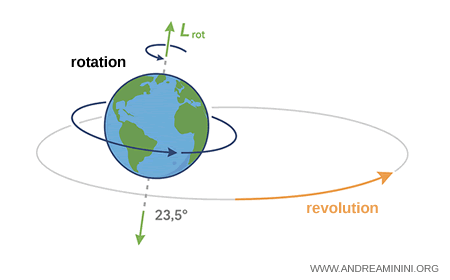
- Momento angular de rotación
La primera contribución proviene del giro de la Tierra sobre su propio eje, un movimiento que se completa aproximadamente cada 24 horas. El valor de este momento angular depende de la masa del planeta, de su radio, de cómo se distribuye esa masa en el interior y de la velocidad angular $ \omega $. Gracias a esta rotación, el eje terrestre se mantiene estable y el ciclo día-noche conserva una regularidad prácticamente constante a lo largo de enormes escalas temporales.Nota. Para un cuerpo rígido, el momento angular de rotación se expresa como $$ L_{\text{rot}} = I \omega $$ donde $ I $ es el momento de inercia y $ \omega $ la velocidad angular. En el caso de una esfera ligeramente achatada como la Tierra, suele emplearse la aproximación $$ I \approx \frac{2}{5} M R^2 $$ junto con $$ \omega = \frac{2\pi}{T_{\text{rot}}} $$ siendo $ T_{\text{rot}} \approx 24,\text{h} $.
- Momento angular orbital
La segunda forma procede del movimiento de traslación alrededor del Sol, que dura cerca de 365 días. Aquí, el momento angular depende de la masa terrestre, de la distancia media al Sol y de la velocidad orbital del planeta. Esta magnitud es decisiva para mantener la órbita estable y evitar desviaciones que alterarían el equilibrio del sistema Tierra-Sol. Para un cuerpo en órbita, el momento angular se escribe como $$ L_{\text{orb}} = m v r $$ o, en forma vectorial, $$ \mathbf{L}_{\text{orb}} = \mathbf{r} \times \mathbf{p} $$ donde $ m $ es la masa de la Tierra, $ v $ su velocidad orbital y $ r $ la distancia media al Sol.Nota. Dado que el movimiento orbital cumple $ v = \omega_{\text{orb}} r $, el momento angular también puede expresarse como $$ L_{\text{orb}} = m, r^2, \omega_{\text{orb}} $$ con $ \omega_{\text{orb}} = \frac{2\pi}{T_{\text{orb}}} $ y $ T_{\text{orb}} \approx 365,\text{giorni} $.
Ambas formas de movimiento están ligadas por una misma ley física: la conservación del momento angular. Este principio explica por qué la Tierra mantiene un eje de rotación casi invariable y una órbita estable a lo largo del tiempo.
Y así sucesivamente.