Torque

Torque (o momento de una fuerza) es la capacidad que tiene una fuerza para provocar la rotación de un objeto alrededor de un punto o de un eje. La fórmula fundamental es: $$ M = F \cdot d $$ donde $F$ es la magnitud de la fuerza y $d$ es el brazo de palanca (o radio), es decir, la distancia perpendicular entre la línea de acción de la fuerza y el punto de giro (o eje de rotación).

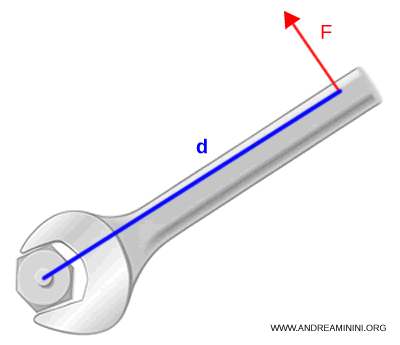
Si la fuerza no se aplica perpendicularmente, el torque se calcula mediante: $$ M = F \cdot d \cdot \sin \theta $$ donde $\theta$ es el ángulo entre la dirección de la fuerza y el brazo de palanca.

Por lo tanto, para determinar el torque no basta con conocer la fuerza: también es necesario precisar el lugar y la dirección en que se aplica con respecto al eje de rotación.

Por convención, el torque se considera:

• positivo $(M > 0)$ cuando la rotación es en sentido antihorario,
• negativo $(M < 0)$ cuando la rotación es en sentido horario.

Sin embargo, la convención de signos puede variar según el contexto.

Nota. Cuando actúan varios torques simultáneamente, el signo de cada uno se asigna según el efecto que produciría si actuara de manera aislada. El torque resultante se obtiene como la suma algebraica de todos los torques individuales.

Ejemplo

Imaginemos que utilizo una llave de 0.3 m para aflojar un tornillo aplicando una fuerza de 20 N de manera perpendicular al brazo.

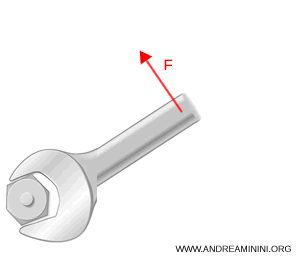
El torque sobre el tornillo es de 6 N·m (newton-metro):

$$ M = 20 \times 0.3 = 6 \, \text{N·m} $$

Si en cambio empleo una llave más larga, de 0.6 m, aplicando la misma fuerza de 20 N de forma perpendicular,

$$ M = 20 \times 0.6 = 12 \, \text{N·m} $$

el torque se duplica.

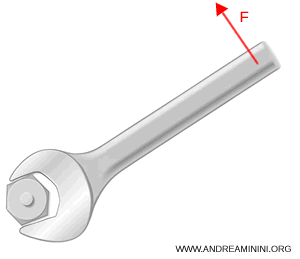
Esto muestra claramente que cuanto más alejada del eje se aplica la fuerza, más sencillo resulta girar el tornillo.

En pocas palabras: una llave más larga permite realizar el mismo trabajo con menos esfuerzo, porque incrementa el torque sin necesidad de aumentar la fuerza.

Nota. El mismo principio explica por qué las manillas de las puertas se colocan lejos de las bisagras. Empujar cerca de las bisagras exige mucha más fuerza que hacerlo en la manilla.

Por ejemplo, aplicar una fuerza de 10 N a 1 metro de las bisagras genera un torque de 10 N·m: $$ M = F \times d = 10 \ N \times 1 \ m = 10 \, \text{N·m} $$ Pero si empujo a solo 0.2 m de las bisagras, para obtener el mismo torque ($ M = 10 \ N \cdot m $) necesitaría cinco veces más fuerza: $$ F = \frac{M}{d} = \frac{10 \ N \cdot m}{0.2 \ m} = 50 \, \text{N} $$

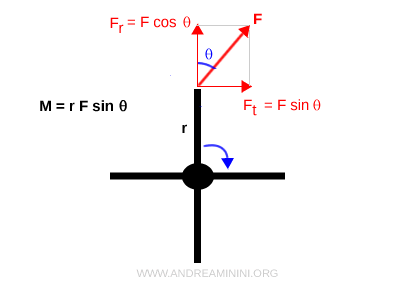
La fórmula del torque

Una fuerza $\vec{F}$ aplicada en un punto situado a una distancia $ r $ del eje de rotación de un cuerpo rígido puede inducir su giro. Este efecto rotacional se mide mediante el torque $M$, definido como: $$ M = r F \sin \theta $$ donde $\theta$ es el ángulo entre el vector de posición y la dirección de la fuerza.

Si la fuerza se aplica radialmente-es decir, a lo largo del radio que une el punto de aplicación con el eje de rotación-el torque es nulo: $ M = 0 $.

En este caso, no se produce rotación alguna.

En cambio, si la fuerza se aplica de forma perpendicular al radio, el torque se maximiza, ya que toda la magnitud de la fuerza contribuye al giro.

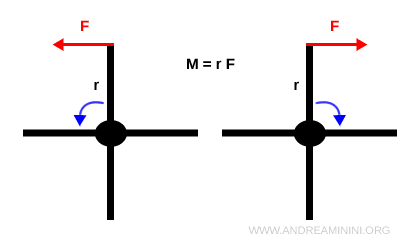
En general, solo la componente tangencial de una fuerza produce rotación; la componente radial no tiene efecto.

Por ello, el torque se calcula proyectando la fuerza en la dirección tangencial:

$$ M = r \, (F \sin \theta) $$

La componente radial se descarta.

Ejercicios

Ejercicio 1

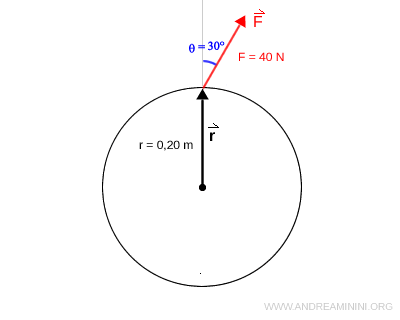
Determina el torque generado por una fuerza de $ F=40 \ N $ aplicada a una distancia de $ r = 0.20 \ m $ del eje de rotación, con un ángulo de 30° respecto al brazo de palanca.

La fórmula del torque es:

$$ M = r \cdot F \cdot \sin \theta $$

Aquí, $ r $ es la distancia al eje de rotación, es decir, la longitud del brazo de palanca $ \vec{r} $. En este caso, $ r = 0.20 \ m $.

$$ M = 0.20 \ m \cdot F \cdot \sin \theta $$

La fuerza aplicada es $ F = 40 \ N $

$$ M = 0.20 \ m \cdot 40 \ N \cdot \sin \theta $$

El ángulo entre el vector de la fuerza $ \vec{F} $ y el brazo de palanca $ \vec{r} $ es $ \theta = 30° $.

$$ M = 0.20 \ m \cdot 40 \ N \cdot \sin 30° $$

Como $ \sin 30° = \tfrac{1}{2} $,

$$ M = 0.20 \ m \cdot 40 \ N \cdot \tfrac{1}{2} $$

Esto nos da la componente tangencial de la fuerza: $ F_x = 40 \ N \cdot \tfrac{1}{2} = 20 \ N $

$$ M = 0.20 \ m \cdot 20 \ N $$

Por lo tanto, el torque es de 4 newton-metro.

$$ M = 4 \ Nm $$

Y así sucesivamente.