Las palancas en física

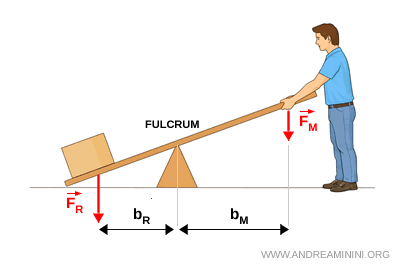
A cada fuerza le corresponde un brazo de palanca, definido como la distancia perpendicular entre el punto de apoyo y la línea de acción de la fuerza. Indicamos:

• \( b_M \), el brazo de la fuerza aplicada;
• \( b_R \), el brazo de la fuerza resistente.

La fuerza aplicada \( F_M \) y la fuerza resistente \( F_R \) quedan compensadas por la reacción ejercida en el punto de apoyo.

Para que la palanca se encuentre en equilibrio estático, el momento total que actúa sobre ella debe ser nulo cuando se toma el punto de apoyo como eje de rotación.

$$ b_R F_R = b_M F_M $$

Esta relación muestra de forma clara que la intensidad de una fuerza puede reducirse aumentando su brazo de palanca, o incrementarse si dicho brazo se acorta.

Por ejemplo, al levantar un objeto pesado, conviene aplicar la fuerza \( F_M \) lo más lejos posible del punto de apoyo. Así se aumenta el brazo \( b_M \) y se necesita ejercer una fuerza menor.

Desde un punto de vista práctico, las palancas son máquinas simples que permiten equilibrar o amplificar fuerzas para levantar, mover o vencer una resistencia con mayor eficacia.

Un ejemplo práctico

Consideremos una palanca en equilibrio, para la cual se cumple la relación:

$$ b_R F_R = b_M F_M $$

Supongamos que la fuerza resistente es

$$ F_R = 100\ \text{N} $$

y que su brazo de palanca es

$$ b_R = 0.20\ \text{m} $$

Si la fuerza aplicada actúa a una distancia de un metro del punto de apoyo, es decir, $ b_M = 1.00\ \text{m} $, la fuerza aplicada necesaria será:

$$ F_M = \frac{b_R}{b_M} F_R = \frac{0.20}{1.00} \cdot 100 = 20\ \text{N} $$

La fuerza aplicada resulta, por tanto, mucho menor que la fuerza resistente.

Nota. Si la fuerza aplicada se ejerciera a solo diez centímetros del punto de apoyo, es decir, $ b_M = 0.10\ \text{m} $, la fuerza necesaria sería mucho mayor $$  F_M = \frac{0.20}{0.10} \cdot 100 = 200\ \text{N} $$ En este caso, la fuerza aplicada debe ser superior a la fuerza resistente.

En resumen, para una misma fuerza resistente, aumentar el brazo de la fuerza aplicada reduce la fuerza necesaria, mientras que disminuirlo produce el efecto contrario.

Palancas ventajosas, desventajosas y neutras

Según la relación entre las longitudes de los brazos, una palanca puede clasificarse como ventajosa, desventajosa o neutra.

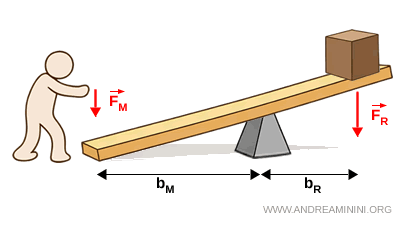
• Palanca ventajosa
  Una palanca es ventajosa cuando el brazo de la fuerza aplicada es mayor que el de la fuerza resistente $$
  b_M > b_R $$ En este caso, el equilibrio se logra con una fuerza aplicada menor que la fuerza resistente $$ F_M < F_R $$ La palanca permite vencer una gran resistencia aplicando una fuerza más pequeña.
  
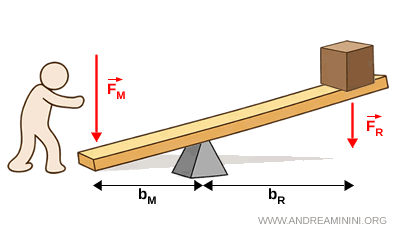
• Palanca desventajosa
  Una palanca es desventajosa cuando el brazo de la fuerza aplicada es menor que el de la fuerza resistente $$ b_M < b_R
  $$ En este caso, el equilibrio requiere una fuerza aplicada mayor que la fuerza resistente $$ F_M > F_R
  $$ Aunque no reduce la fuerza necesaria, este tipo de palanca es útil cuando se busca mayor precisión o mayor rapidez en el movimiento.
  
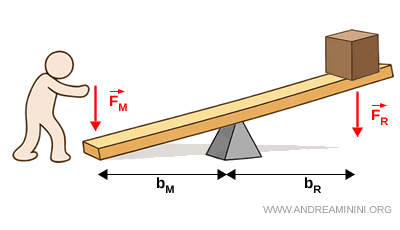
• Palanca neutra
  Una palanca es neutra cuando ambos brazos tienen la misma longitud $$ b_M = b_R $$ En este caso, la fuerza aplicada es igual a la fuerza resistente $$ F_M = F_R $$ No se obtiene ni ventaja ni desventaja mecánica en términos de fuerza.
  

Tipos de palancas

Las palancas se agrupan en tres tipos según la posición relativa del punto de apoyo, la fuerza aplicada y la fuerza resistente.

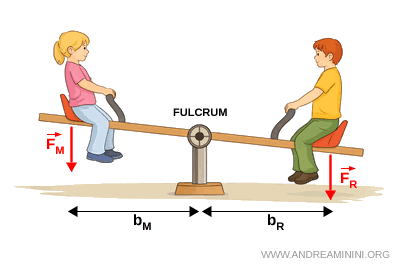
• Palanca de primer género
  El punto de apoyo se sitúa entre la fuerza aplicada y la fuerza resistente. Este tipo de palanca puede ser ventajoso, desventajoso o neutro. Ejemplos comunes son las tijeras y los balancines de los parques infantiles.
  
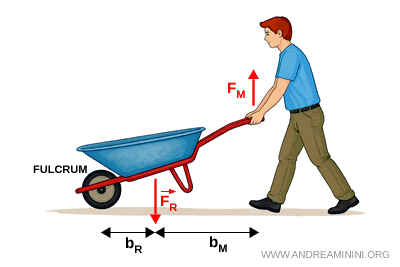
• Palanca de segundo género
  La fuerza resistente se encuentra entre el punto de apoyo y la fuerza aplicada. Este tipo de palanca es siempre ventajoso. Ejemplos habituales son las carretillas, los cascanueces y los abridores de botellas.
  
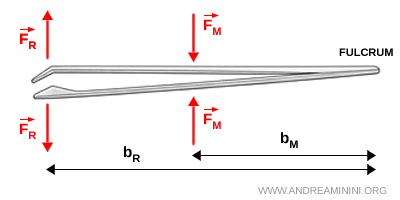
• Palanca de tercer género
• La fuerza aplicada se sitúa entre el punto de apoyo y la fuerza resistente. Este tipo de palanca es siempre desventajoso, ya que el brazo $ b_R $ es mayor que el brazo $ b_M $, pero permite realizar movimientos rápidos y precisos. Un ejemplo típico son las pinzas.
  

Estas tres clases de palancas muestran que la posición de las fuerzas suele ser más importante que su magnitud.

Gracias a un uso adecuado de los brazos de palanca, una fuerza pequeña puede vencer a otra mucho mayor.

Un ejemplo práctico

Un trabajador utiliza una palanca rígida para levantar una caja con una masa de 75 kg.

La caja está situada a 0.40 m del punto de apoyo, mientras que el trabajador aplica la fuerza motriz en el extremo opuesto de la palanca, a una distancia de 1.60 m del punto de apoyo.

Los datos del problema son:

• \( b_R = 0.40 \ \text{m} \)
• \( b_M = 1.60 \ \text{m} \)
• \( m = 75 \ \text{kg} \)

¿Cuál es el valor de la fuerza resistente ejercida por la caja?

La fuerza resistente coincide con el peso de la caja:

$$ F_R = P = mg $$

La masa es $ m = 75 \ \text{kg} $ y la aceleración de la gravedad vale \( g = 9.8 \ \text{N/kg} \).

$$ F_R = 75 \ (\text{kg}) \cdot 9.8 \ (\text{N/kg}) = 735 \ \text{N} $$

Por tanto, la fuerza resistente que actúa sobre la palanca tiene un valor de:

$$ F_R = 735 \ \text{N} $$

¿Qué fuerza motriz debe aplicar el trabajador para mantener la palanca en equilibrio?

La condición de equilibrio estático de una palanca es:

$$ b_R F_R = b_M F_M $$

Despejando la fuerza motriz \( F_M \):

$$ F_M = \frac{b_R}{b_M} F_R = \frac{0.40}{1.60} \cdot 735 $$

$$ F_M = 0.25 \cdot 735 = 183.75 \ \text{N} \approx 184 \ \text{N} $$

Por consiguiente, la fuerza motriz necesaria para mantener el equilibrio es:

$$ F_M \approx 184 \ \text{N} $$

¿De qué tipo de palanca se trata?

Una palanca se considera mecánicamente ventajosa cuando \( b_M > b_R \).

En este caso, $ b_M = 1.60 \ \text{m} $ y $ b_R = 0.40 \ \text{m} $, por lo que se trata de una palanca mecánicamente ventajosa.

La ventaja mecánica es, por tanto:

$$ \frac{F_R}{F_M} = \frac{b_M}{b_R} = \frac{1.60}{0.40} = 4 $$

Esto significa que la fuerza motriz es aproximadamente cuatro veces menor que la fuerza resistente.

Ejercicio 2

Un saco con una masa de $ m = 200 \ \text{kg} $ se coloca en uno de los extremos de una palanca de primer género. En el extremo opuesto, un trabajador aplica una fuerza motriz de $ F_M = 200 \ \text{N} $.

¿A qué distancia del saco debe situarse el punto de apoyo para que la palanca se mantenga en equilibrio estático?

La condición de equilibrio de una palanca es:

$$ b_R F_R = b_M F_M $$

La fuerza motriz es conocida y vale $ F_M = 200 \ \text{N} $.

$$ b_R F_R = b_M \cdot 200 \ (\text{N}) $$

La fuerza resistente viene dada por el peso del saco:

$$ F_R = mg = 200 \ (\text{kg}) \cdot 9.81 \ (\text{N/kg}) = 1962 \ \text{N} $$

Sustituyendo $ F_R = 1962 \ \text{N} $ en la ecuación de equilibrio, se obtiene:

$$ b_R \cdot (1962 \ \text{N}) = b_M \cdot 200 \ (\text{N}) $$

$$ b_R \cdot 1962 = b_M \cdot 200 $$

Despejando el brazo resistente $ b_R $:

$$ b_R = \frac{b_M \cdot 200}{1962} $$

$$ b_R = b_M \cdot 0.102 $$

Dado que la longitud total de la palanca es $ L = b_R + b_M = 3.00 \ \text{m} $, el brazo motriz puede expresarse como:

$$ b_M = 3.00 \ \text{m} - b_R $$

Sustituyendo en la expresión anterior:

$$ b_R = (3.00 \ \text{m} - b_R) \cdot 0.102 $$

$$ b_R = 0.306 \ \text{m} - 0.102 \, b_R $$

$$ b_R + 0.102 \, b_R = 0.306 \ \text{m} $$

$$ b_R \cdot 1.102 = 0.306 \ \text{m} $$

$$ b_R = \frac{0.306 \ \text{m}}{1.102} $$

$$ b_R \approx 0.28 \ \text{m} $$

En condiciones de equilibrio, el punto de apoyo debe situarse, por tanto, a una distancia de $ 0.28 \ \text{m} $ del saco.

Para completar el análisis, la longitud del brazo motriz es:

$$ b_M = 3.00 - 0.28 = 2.72 \ \text{m} $$

La palanca es mecánicamente ventajosa, ya que el brazo motriz es claramente mayor que el brazo resistente ( $ b_M > b_R $ ).  

Ejercicio 3

Un abridor de botellas con una longitud total de 10 cm se utiliza para retirar el tapón metálico de una botella.

La distancia entre el punto de apoyo y el punto de contacto con el tapón es de 2 cm, y el tapón ejerce una fuerza resistente de 100 N.

¿Qué fuerza motriz debe aplicarse en el extremo libre del abridor?

Para simplificar el análisis, se introduce un sistema de referencia cartesiano xy, haciendo coincidir el eje x con el eje longitudinal del abridor.

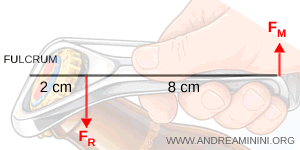
La palanca se encuentra en equilibrio cuando los momentos de las fuerzas respecto al punto de apoyo son iguales en magnitud:

$$ b_R F_R = b_M F_M $$

Las magnitudes conocidas son $ b_R = 2 \ \text{cm} = 0.02 \ \text{m} $, $ b_M = (10 - 2) \ \text{cm} = 0.08 \ \text{m} $ y $ F_R = 100 \ \text{N} $.

$$ (0.02 \ \text{m}) \cdot (100 \ \text{N}) = (0.08 \ \text{m}) \cdot F_M $$

Se simplifica la expresión eliminando la unidad de longitud $ \text{m} $ en ambos miembros de la ecuación.

$$ 0.02 \cdot (100 \ \text{N}) = 0.08 \cdot F_M $$

Resolviendo la ecuación respecto de la fuerza motriz, se obtiene:

$$ F_M = \frac{0.02 \cdot (100 \ \text{N})}{0.08} = 25 \ \text{N} $$

Por lo tanto, para abrir la botella es necesario aplicar en el extremo del abridor una fuerza motriz de al menos 25 N.

En situaciones reales, la fuerza requerida debe ser ligeramente mayor que este valor teórico para compensar el rozamiento, las deformaciones elásticas y otras pérdidas mecánicas.

Y así sucesivamente.