Operador de paridad

El operador de paridad es el operador matemático que describe la reflexión espacial, es decir, la transformación que invierte las coordenadas espaciales de un sistema con respecto al origen.

En términos sencillos, aplicar la paridad significa sustituir una configuración física por su imagen especular, obtenida al invertir la orientación del espacio.

Por ejemplo, si un punto del espacio tiene coordenadas

$$ x = (x, y, z) $$

la acción del operador de paridad $ P $ viene dada por

$$ P(x) = (-x, -y, -z) $$

Esta transformación se conoce como inversión espacial.

Aplicar el operador de paridad a un sistema físico equivale, por tanto, a observarlo como si se reflejara en un espejo situado en el origen, y no respecto a un plano.

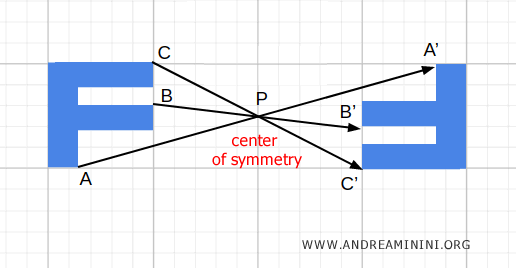
Desde un punto de vista geométrico, esto corresponde a una simetría central. Se trata de una transformación global que invierte simultáneamente izquierda y derecha, delante y detrás, arriba y abajo.

¿Para qué se utiliza?

El operador de paridad desempeña un papel fundamental en física, ya que la paridad se conserva en algunas interacciones fundamentales, mientras que en otras se rompe.

• Si un proceso físico permanece invariante bajo esta transformación, se dice que la paridad se conserva.
• Si el proceso cambia, se dice que la paridad se viola.

El operador de paridad constituye así una herramienta esencial para clasificar sistemas físicos y partículas.

Nota. En las interacciones electromagnéticas y fuertes, la paridad se conserva. En cambio, en las interacciones débiles, la paridad se viola. En este contexto, la naturaleza distingue entre izquierda y derecha. Precisamente por ello existen únicamente neutrinos levógiros y antineutrinos dextrógiros. La violación de la paridad pone de manifiesto una de las asimetrías más profundas de la naturaleza.

Propiedades fundamentales

El operador de paridad presenta varias propiedades fundamentales.

Si se aplica dos veces, el operador de paridad devuelve el sistema a su configuración original.

$$ P^2 = I $$

donde $ I $ representa el operador identidad.

Ejemplo. Consideremos un punto del espacio con coordenadas: \[ \vec r = (2,-1,3) \] El operador de paridad invierte todas las coordenadas: \[ P(\vec r) = (-2,1,-3) \] Esto corresponde a una reflexión del punto con respecto al origen. Si aplicamos nuevamente el operador de paridad, obtenemos: \[ P(P(\vec r)) = P(-2,1,-3) = (2,-1,3) \] Recuperamos así el punto original, es decir, \( P^2 = I \). \[ P^2(\vec r) = \vec r \]

Desde un punto de vista físico, esto significa que realizar dos veces una inversión espacial equivale a no realizar ninguna transformación. El sistema regresa a su configuración inicial.

Por esta razón, el operador de paridad $ P $ solo puede tener dos valores propios:

• +1, correspondiente a un estado de paridad par.
• -1, correspondiente a un estado de paridad impar.

Vectores polares y vectores axiales

El operador de paridad permite además distinguir entre vectores polares y vectores axiales.

• Vectores polares
  Un vector polar, como la posición, la velocidad o la fuerza, cambia de signo bajo una inversión espacial: $$ P(\vec{v}) = -\vec{v} $$
• Vectores axiales (seudovectores)
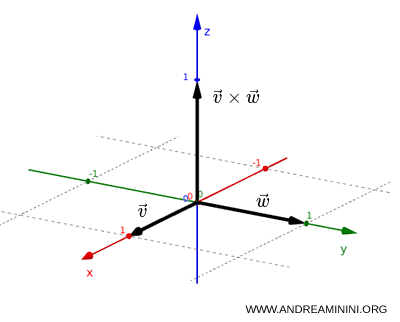
  Un vector axial, también llamado seudovector (pseudovector), como el momento angular o el campo magnético, no cambia de signo bajo una inversión espacial: $$ P(\vec v \times \vec w) = (-\vec v) \times (-\vec w) = \vec v \times \vec w = \vec L $$

  Demostración. Sea \( \vec L = \vec v \times \vec w \), donde \( \vec v \) y \( \vec w \) son vectores polares. Bajo la acción del operador de paridad \( P \) se cumple que $$ P(\vec v) = -\vec v, \quad P(\vec w) = -\vec w $$ y, por tanto, $$ P(\vec L) = \vec L $$ Ejemplo. Consideremos dos vectores en el plano: $$ \vec v = (1,0), \qquad \vec w = (0,1) $$ Su producto vectorial es un vector perpendicular al plano, dirigido a lo largo del eje z: $$ \vec v \times \vec w = (0,0,1) $$ Este vector es un vector axial. Al aplicar la inversión espacial se obtiene: $$ (x,y) \rightarrow (-x,-y) $$ y, por tanto: $$ P(\vec v) = (-1,0), \quad P(\vec w) = (0,-1) $$ Recalculando el producto vectorial: $$ P(\vec v) \times P(\vec w) = (-1,0) \times (0,-1) = (0,0,1) $$ El resultado permanece invariante: $$ P(\vec v \times \vec w) = \vec v \times \vec w $$ La dirección del vector se conserva. Físicamente, la inversión espacial invierte las direcciones, pero no el sentido de rotación.
  

Escalares y pseudoescalares

El operador de paridad también permite distinguir entre magnitudes escalares y pseudoescalares.

• Escalar
  Una magnitud se denomina escalar si no cambia de signo bajo una inversión espacial.

  Ejemplo. La temperatura en un punto es \( T = 20^\circ \text{C} \). Si aplicamos una inversión espacial, la temperatura permanece inalterada: $$ P(T) = T $$ La temperatura no posee dirección ni orientación espacial. Por ello conserva el mismo valor y el mismo signo en la configuración reflejada. Esto la convierte en una magnitud escalar.

• Pseudoescalar
  Una magnitud se denomina pseudoescalar si cambia de signo bajo una inversión espacial.

  Ejemplo. Consideremos tres vectores: \[ \vec a = (1,0,0) \\ \vec b = (0,1,0) \\ \vec c = (0,0,1) \] Calculemos el producto mixto: \[ S = \vec a \cdot (\vec b \times \vec c) \] Dado que \( \vec b \times \vec c = (1,0,0) \), obtenemos: \[ S = \vec a \cdot (\vec b \times \vec c) = 1 \] A continuación aplicamos la paridad: \[ P(\vec a) = (-1,0,0), \quad P(\vec b) = (0,-1,0), \quad P(\vec c) = (0,0,-1) \] Calculamos entonces: \[ P(S) = P(\vec a) \cdot (P(\vec b) \times P(\vec c)) \] \[ P(S) = (-1,0,0) \cdot \big( (0,-1,0) \times (0,0,-1) \big) \] Dado que \( (0,-1,0) \times (0,0,-1) = (1,0,0) \), se obtiene: \[ P(S) = (-1,0,0) \cdot (1,0,0) = -1 \] El resultado final cambia de signo. Este es un ejemplo claro de una magnitud pseudoescalar.

Autovalores de paridad de escalares, pseudoescalares, vectores y pseudovectores

El operador de paridad \( P \) describe cómo se comportan las magnitudes físicas cuando se invierten las coordenadas del espacio. A cada magnitud se le asigna un autovalor de paridad bien definido, que solo puede ser +1 o -1.

Los escalares no se ven afectados por la inversión espacial y, por esta razón, tienen asociado el autovalor +1.  Los pseudoescalares, en cambio, cambian de signo bajo una transformación de paridad y se caracterizan por el autovalor -1.

Magnitud	Transformación de paridad	Autovalor
Escalar	\( P(s)=s \)	\( +1 \)
Pseudoescalar	\( P(p)=-p \)	\( -1 \)
Vector (o vector polar)	\( P(\vec v)=-\vec v \)	\( -1 \)
Pseudovector (o vector axial)	\( P(\vec a)=\vec a \)	\( +1 \)

Esta misma regla se aplica a los vectores ordinarios, también conocidos como vectores polares, como el desplazamiento o la velocidad. Al efectuar una operación de paridad, estos vectores invierten su orientación en el espacio y, por ello, quedan asociados al autovalor -1.

En contraste, los pseudovectores, o vectores axiales, como el momento angular, permanecen inalterados bajo la inversión espacial. Por esta razón, se les asigna el autovalor +1.

En resumen, los escalares y los pseudovectores son invariantes frente a la inversión espacial, es decir, frente a una transformación de paridad, mientras que los pseudoescalares y los vectores polares cambian de signo.

Paridad en las partículas

La paridad es un número cuántico que caracteriza a las partículas, al mismo nivel que el espín, la carga eléctrica, el isoespín, la extrañeza y otras magnitudes fundamentales. 

Indica cómo se transforma el estado cuántico de una partícula cuando se realiza una inversión espacial, es decir, cuando se invierten todas las coordenadas del espacio.

Este concepto permite establecer diferencias claras entre las principales familias de partículas elementales.

• En el caso de los fermiones (partículas con espín semientero), la paridad de una partícula es opuesta a la de su antipartícula.
• Por el contrario, en los bosones (partículas con espín entero), la partícula y su antipartícula comparten la misma paridad.

En las partículas compuestas, la paridad total se obtiene multiplicando las paridades de cada uno de sus constituyentes. Por esta razón, la paridad es un número cuántico de tipo multiplicativo. Esto la diferencia de otros números cuánticos, como la carga eléctrica o la extrañeza, que se combinan de forma aditiva.

Hadrones

Dado que la interacción fuerte conserva la paridad, los hadrones, es decir, bariones y mesones, son autoestados del operador de paridad. Por ello, pueden clasificarse según el valor propio asociado:

$$ p = \pm 1 $$

Bariones

Por convención, se asigna a los quarks una paridad intrínseca positiva:

$$ p(\text{quark}) = +1 $$

Como consecuencia, un barión formado por tres quarks tiene paridad:

$$ p = (+1)^3 = +1 $$

Esto explica que los bariones en su estado fundamental presenten paridad positiva.

Mesones

Los mesones están compuestos por un quark y un antiquark. Dado que el antiquark posee una paridad intrínseca opuesta a la del quark, la paridad de un mesón en su estado fundamental es -1:

$$ p = (+1) \cdot (-1) = -1 $$

En los mesones excitados entra en juego una contribución adicional asociada al momento angular orbital $ l $. En este caso, la paridad viene dada por:

$$ p = (-1)^{l+1} $$

Aquí $ l $ representa el momento angular orbital correspondiente al movimiento relativo entre el quark y el antiquark.

Fotón

El fotón es una partícula vectorial con espín 1, asociada al potencial vectorial electromagnético. Su paridad intrínseca es -1:

$$ p = -1 $$

En el caso del fotón, la paridad intrínseca no es directamente observable del mismo modo que en las partículas con masa. En su lugar, se define a partir de cómo se transforma el campo electromagnético bajo una inversión espacial.

Y así sucesivamente.