Neutrinos
El neutrino, representado por la letra griega $\nu$, es una partícula elemental que pertenece a la familia de los leptones. Carece de carga eléctrica, posee una masa en reposo extraordinariamente pequeña (mucho menor que la de cualquier otra partícula con masa distinta de cero) y un espín $1/2$, lo que lo clasifica como un fermión.
Estas propiedades lo convierten en una partícula casi “fantasmal”: no responde a la fuerza electromagnética, no se ve afectado por la interacción nuclear fuerte y puede atravesar la materia prácticamente sin obstáculos.
Los neutrinos solo interactúan mediante la fuerza nuclear débil y la gravedad, aunque esta última resulta despreciable por su masa ínfima.
Se generan en una gran variedad de procesos, tanto naturales como artificiales: durante el decaimiento beta de núcleos atómicos y hadrones, en la fusión nuclear en el interior de las estrellas (incluido nuestro Sol), en reactores nucleares, en las colisiones de rayos cósmicos con la atmósfera terrestre y en aceleradores de partículas.
Nota. Su capacidad de penetración es realmente sorprendente: cada segundo, miles de millones de neutrinos solares atraviesan cada centímetro cuadrado de la Tierra sin detenerse. En el núcleo solar, la fusión transforma hidrógeno en helio, liberando enormes cantidades de neutrinos electrónicos; aproximadamente $ 6.5 \times 10^{10} \ \text{neutrinos} / (\text{cm}^2 \cdot \text{s}) $ llegan a la superficie terrestre. Dicho de otra manera, decenas de miles de millones atraviesan un área tan pequeña como una uña en apenas un segundo, sin producir ningún efecto perceptible.

Por qué se llaman neutrinos
El nombre alude a su carga eléctrica neutra y establece un paralelismo con el neutrón, un nucleón más grande y masivo presente en el núcleo atómico.
Al igual que el neutrino, el neutrón carece de carga eléctrica positiva o negativa.
Diferencias entre neutrinos y neutrones
El neutrón es mucho más pesado e interactúa mediante la fuerza nuclear fuerte, mientras que el neutrino lo hace únicamente a través de la interacción débil.
La masa exacta del neutrino sigue siendo desconocida. Algunas estimaciones sugieren que podría ser un millón de veces más ligera que la del electrón.
Otras proyecciones la sitúan en valores de solo decenas de miles de veces más pequeña.
Nota. Si, en un escenario hipotético, la masa de un neutrino fuese un millón de veces menor que la de un electrón, y teniendo en cuenta que la masa del electrón es 1835 veces menor que la de un neutrón (véase el núcleo atómico), un neutrino resultaría aproximadamente dos mil millones de veces más ligero que un neutrón.

Determinar con precisión la masa del neutrino constituye uno de los grandes retos de la astrofísica. La masa total de todos los neutrinos del Universo podría contribuir, al menos en parte, a explicar el origen de la materia oscura.
Propiedades de los neutrinos
A continuación se presenta una tabla de referencia que resume sus principales características físicas.
| Propiedad | Valor / Descripción |
|---|---|
| Símbolo | ν (neutrino), ν̄ (antineutrino) |
| Sabores (tipos) | νe, νμ, ντ |
| Número leptónico | νe: Le=+1, νμ: Lμ=+1, ντ: Lτ=+1 Antineutrinos: los sabores correspondientes con número leptónico -1 |
| Carga eléctrica | 0 (eléctricamente neutro) |
| Espín | ½ (fermiones, obedecen las estadísticas de Fermi-Dirac) |
| Masa en reposo | No nula pero extremadamente pequeña (« 1 eV/c2); solo se han medido diferencias de masa, no valores absolutos |
| Interacciones | Fuerza débil (mediada por los bosones W⊃± y Z0) y gravedad (irrelevante a escala subatómica) |
| Helicidad / Quiralidad | Todos los neutrinos observados son zurdos; todos los antineutrinos observados son diestros |
| Oscilaciones | Pueden cambiar de sabor mientras se propagan (mezcla PMNS) |
| Sección eficaz típica | ∼10-44 m2 a energías del orden de MeV (crece con la energía en este rango) |
| Transparencia frente a la materia | Interactúan tan raramente que pueden atravesar cantidades enormes de materia sin dispersarse |
Las masas absolutas de los neutrinos siguen sin conocerse. Solo se dispone de límites superiores, ya que dar valores concretos sería meramente especulativo.
Sabores, antineutrinos y números leptónicos
Existen tres “sabores” de neutrinos, cada uno asociado a un leptón cargado de la misma familia:
| Sabor de neutrino | Símbolo | Leptón asociado |
|---|---|---|
| Neutrino electrónico | \(\nu_e\) | Electrón |
| Neutrino muónico | \(\nu_{\mu}\) | Muón |
| Neutrino tau | \(\nu_{\tau}\) | Tau |
Un neutrino creado con un sabor específico no necesariamente conserva esa identidad a lo largo de su recorrido. Este fenómeno se conoce como oscilación de neutrinos.
Cada neutrino posee un número leptónico bien definido.
A cada neutrino le corresponde una antipartícula, denominada antineutrino, que lleva el número leptónico opuesto.
| Partícula | Símbolo | Nombre | Número leptónico |
|---|---|---|---|
| Neutrino electrónico | \(\nu_e\) | Neutrino electrónico | +1 |
| Neutrino muónico | \(\nu_{\mu}\) | Neutrino muónico | +1 |
| Neutrino tau | \(\nu_{\tau}\) | Neutrino tau | +1 |
| Antineutrino electrónico | \(\bar{\nu}_e\) | Antineutrino electrónico | -1 |
| Antineutrino muónico | \(\bar{\nu}_{\mu}\) | Antineutrino muónico | -1 |
| Antineutrino tau | \(\bar{\nu}_{\tau}\) | Antineutrino tau | -1 |
¿Qué es el número leptónico? Se trata de un número cuántico asignado a todas las partículas de la familia de los leptones y que sirve para llevar el balance en las reacciones. En el Modelo Estándar, el número leptónico total se conserva: la suma antes y después de cualquier interacción debe coincidir. En términos generales, las reglas son:
- Los leptones (electrón, muón, tau y sus respectivos neutrinos) tienen número leptónico $+1$.
- Los antileptones (positrón, antimuón, antitau y antineutrinos) tienen número leptónico $-1$.
- Las demás partículas (quarks, fotones, gluones, etc.) tienen número leptónico $0$.
Neutrinos y antineutrinos intervienen en numerosos procesos nucleares, tanto naturales como en el laboratorio.
Ejemplo
En el decaimiento beta⁻, un neutrón del núcleo se transforma en un protón.
En esta transformación se emiten un electrón y un antineutrino electrónico:
$$ n \rightarrow p + e^- + \bar{\nu}_e $$
A la izquierda de la ecuación, el neutrón $n$ tiene número leptónico $0$.
A la derecha aparecen:
- un protón $p$ con número leptónico $0$
- un electrón $e^-$ con número leptónico $+1$
- un antineutrino electrónico $\bar{\nu}_e$ con número leptónico $-1$
El número leptónico total a la derecha es:
$$ 0 + 1 + (-1) = 0 $$
Como el balance es $0$ en ambos lados, el número leptónico se conserva.
Esto significa que la reacción está permitida en el marco del Modelo Estándar.
Nota. En el decaimiento beta⁺ ocurre lo inverso: un protón se transforma en un neutrón. En este caso se emiten un positrón (la antipartícula del electrón) y un neutrino electrónico: $$ p \rightarrow n + e^+ + \nu_e $$ También aquí se conserva el número leptónico: $$ p^{(0)} \;\rightarrow\; n^{(0)} \;+\; e^{+\,(-1)} \;+\; \nu_e^{(+1)} $$ Para mayor claridad, el número leptónico de cada partícula aparece indicado como superíndice. La suma en ambos lados sigue siendo $0 + (-1) + (+1) = 0$. Esta reacción también está permitida según el Modelo Estándar.
Por qué los neutrinos atraviesan la materia con tanta facilidad
Los neutrinos cruzan la materia casi sin obstáculos porque interactúan únicamente a través de la fuerza más débil de la naturaleza.
Desde el punto de vista físico, su aparente “invisibilidad” se explica principalmente por tres factores:
- Interacción débil
Al carecer de carga eléctrica, los neutrinos no se sienten atraídos por los protones ni repelidos por los electrones. Solo responden a la gravedad (irrelevante a nivel subatómico) y a la interacción nuclear débil, mucho menos intensa que la fuerza fuerte o el electromagnetismo. Además, la fuerza débil actúa a distancias diminutas -del orden de $10^{-18}$ metros-, lo que reduce aún más la probabilidad de colisión con un nucleón. - Sección eficaz extremadamente reducida
La probabilidad de interacción entre partículas se mide con la sección eficaz ($\sigma$). Para un neutrino típico ($E \approx 1\ \text{MeV}$), esta es del orden de $10^{-44} \ \text{m}^2$, miles de millones de veces menor que la de una partícula cargada. Dicho de otro modo: un neutrino podría atravesar varios años luz de plomo sólido sin sufrir ni una sola interacción. - Masa ínfima
Aunque no son estrictamente sin masa, los neutrinos poseen una masa increíblemente pequeña (menor que $1\ \text{eV}/c^2$). Esto les permite desplazarse a velocidades muy cercanas a la de la luz, reduciendo aún más las posibilidades de interacción: simplemente no “permanecen” el tiempo suficiente cerca de los nucleones como para reaccionar.En la Tierra, por ejemplo, unos 60 mil millones de neutrinos solares atraviesan cada centímetro cuadrado de materia cada segundo, y casi ninguno interactúa.
La combinación de estos factores hace que la probabilidad de que un neutrino interactúe con la materia sea prácticamente nula.
Antecedentes históricos
En 1930, Wolfgang Pauli observó que el decaimiento beta parecía violar la ley de conservación de la energía.
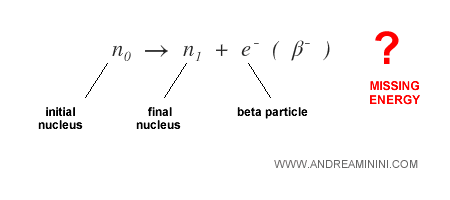
Solo una parte del exceso de energía aparecía en forma de partícula beta; el resto parecía “desaparecer”, lo cual contradecía las leyes de la física.
Para resolver el enigma, Pauli propuso la existencia de una nueva partícula -neutra y con masa extremadamente pequeña- capaz de transportar la energía faltante en el decaimiento β.
Nota. Pauli planteó que un núcleo radiactivo $ A $ podía transformarse en otro ligeramente más ligero $ B $, emitiendo un electrón $ e^- $: $$ A \rightarrow B + e^-$$. Sin embargo, la conservación de la carga implicaba que el núcleo $B$ debía tener una carga positiva mayor que $A$, algo que no se correspondía con los datos experimentales de la época. El neutrón aún no había sido descubierto. Además, la energía del electrón emitido resultaba sistemáticamente inferior a la predicha por la conservación de la energía.
En 1934, Enrico Fermi retomó la hipótesis de Pauli, formuló su teoría del decaimiento beta y bautizó a la partícula como “neutrino”.
Según el modelo de Fermi, en el decaimiento beta un neutrón se convierte en un protón, un electrón y un antineutrino electrónico:
$$ n \rightarrow p^+ + e^- + \bar{\nu}_e $$
Nota. El término “neutrino” fue ideado a modo de diminutivo de “neutrón”, en una conversación entre Enrico Fermi y Edoardo Amaldi en el instituto de la Via Panisperna, en Roma.
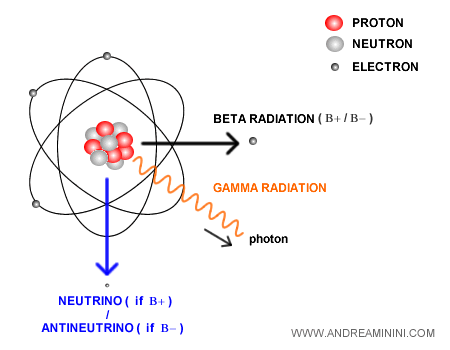
Más adelante se demostró que existen dos tipos principales de neutrinos:
- El neutrino aparece en el decaimiento β⁺, junto con la emisión de un positrón e+. En este proceso, un protón de un núcleo inestable se transforma en un neutrón, emitiendo un positrón y un neutrino electrónico: $$ p \;\longrightarrow\; n + e^+ + \nu_e $$ El proceso inverso del β⁺ es la absorción de un antineutrino electrónico: $$\bar{\nu}_e + p \to n + e^+$$
Nota. Un protón libre no puede experimentar decaimiento β⁺ por conservación de la energía (un neutrón es más pesado que un protón), aunque sí es posible dentro de un núcleo, donde la diferencia de masas nucleares compensa la energía necesaria.
- El antineutrino surge en el decaimiento β⁻, junto con la emisión de un electrón e-. En este proceso, un neutrón -libre o ligado- se transforma en un protón, liberando un electrón y un antineutrino electrónico: $$ n \;\longrightarrow\; p + e^- + \bar{\nu}_e $$ El proceso inverso del β⁻ es la absorción de un neutrino electrónico: $$\nu_e + n \to p + e^-$$
Hacia 1949 se aceptó que los piones $ \pi^- $ decaen en muones y neutrinos, y que los muones $ \mu^- $ a su vez decaen en un electrón ($ e $) y dos neutrinos ($ 2 \nu $):
$$ \pi^- \rightarrow \mu^- + \nu $$
$$ \mu^- \rightarrow e^- + 2\nu $$
En 1953, Konopinski y Mahmoud introdujeron el principio de conservación del número leptónico en todas las interacciones de partículas.
Nota. Según este principio, se asigna $L = +1$ a todos los leptones (electrón, muón, tau y sus neutrinos), $L = -1$ a todos los antileptones (positrón, antimuón, antitau y antineutrinos), y $L = 0$ a todas las demás partículas. Una reacción solo puede tener lugar si el número leptónico total se mantiene constante antes y después de la interacción.
A comienzos de los años cincuenta, el neutrino ya estaba aceptado en la teoría, aunque sin pruebas experimentales directas. Algunos incluso dudaban de su existencia real, considerándolo un artificio matemático.
La primera detección concluyente llegó en 1956, cuando Cowan y Reines observaron el antineutrino electrónico mediante el decaimiento beta inverso:
$$ \bar{\nu} + p^+ \rightarrow n + e^+ $$
A finales de esa década, los físicos se preguntaban si neutrinos y antineutrinos podrían ser en realidad la misma partícula, al ser ambos neutros eléctricamente.
En 1958, Raymond Davis aportó la primera evidencia experimental de que neutrinos y antineutrinos son distintos, confirmando lo que ya sugería la conservación del número leptónico.
Ejemplo. La siguiente reacción está permitida porque la suma de los números leptónicos (mostrados como superíndices) coincide en ambos lados: $$\bar{\nu}^{(-1)} + p^{+(0)} \;\longrightarrow\; n^{(0)} + e^{+( -1 )} $$ En cambio, esta reacción está prohibida porque el número leptónico total no se conserva: $$ \nu^{(+1)} + p^{+(0)} \;\longrightarrow\; n^{(0)} + e^{+( -1 )} $$ Esto demuestra la diferencia esencial entre neutrinos y antineutrinos.
En 1962, un experimento de Lederman, Schwartz y Steinberger ofreció la primera evidencia directa de que existen dos “sabores” distintos de neutrinos: el electrónico y el muónico.
Una vez distinguidos neutrinos y antineutrinos -y sus diferentes sabores-, los decaimientos de piones pudieron escribirse como:
$$ \pi^- \rightarrow \mu^- + \bar{\nu}_\mu $$
$$ \pi^+ \rightarrow \mu^+ + \nu_\mu $$
Los decaimientos de muones toman la forma:
$$ \mu^- \rightarrow e^- + \bar{\nu}_e + \nu_\mu $$
$$ \mu^+ \rightarrow e^+ + \nu_e + \bar{\nu}_\mu $$
Oscilación de neutrinos
La oscilación de neutrinos es un fenómeno cuántico por el cual un neutrino (electrónico, muónico o tauónico) puede cambiar de sabor mientras viaja por el espacio.
En otras palabras, un neutrino electrónico puede transformarse en uno muónico o tauónico, y también a la inversa.
Actualmente se conocen tres tipos (o sabores) de neutrinos:
- $ \nu_e $ (neutrino electrónico)
- $ \nu_{ \mu } $ (neutrino muónico)
- $ \nu_{ \tau } $ (neutrino tauónico)
Estos neutrinos tienen masas distintas -minúsculas, pero en todo caso diferentes de cero-.
Lo esencial es que ninguno de ellos coincide con un único estado de masa. En realidad, cada uno es una superposición cuántica de los tres estados de masa \(\nu_1, \nu_2, \nu_3\), con masas propias \(m_1, m_2, m_3\).
$$ \begin{bmatrix} \nu_e \\ \nu_\mu \\ \nu_\tau \end{bmatrix} = U \begin{bmatrix} \nu_1 \\ \nu_2 \\ \nu_3 \end{bmatrix} $$
Aquí, \(U\) es la matriz PMNS (Pontecorvo-Maki-Nakagawa-Sakata), que contiene los ángulos de mezcla y las fases.
Esto implica que un neutrino producido como \(\nu_e\) es en realidad una combinación de los tres estados de masa. A medida que se propaga, cada estado evoluciona con una fase distinta. La mezcla se modifica con el tiempo, de modo que el neutrino puede llegar a detectarse como \(\nu_\mu\) o \(\nu_\tau\), es decir, con un sabor diferente al inicial.
Los experimentos han confirmado este fenómeno de manera concluyente.
Nota. Este mecanismo dio solución al célebre “problema de los neutrinos solares”: la desconcertante escasez de neutrinos electrónicos solares en comparación con lo previsto por la teoría. La explicación es que muchos de ellos oscilan hacia neutrinos muónicos o tauónicos durante su trayecto del Sol a la Tierra.
La mera existencia de la oscilación demuestra que los neutrinos poseen masa distinta de cero, un descubrimiento sorprendente, ya que el Modelo Estándar original los consideraba partículas sin masa.
Y así continúa la historia.