Constante de estructura fina

La constante de estructura fina, representada por $ \alpha $, es una magnitud fundamental, pura y adimensional. Su valor, aproximadamente $ \alpha = 1/137 $, determina la intensidad con la que interactúan electromagnéticamente las partículas cargadas. Se define mediante la expresión: \[ \alpha = \frac{e^2}{4 \pi \varepsilon_0 \hbar c} \]

En esta fórmula intervienen:

• \( e \): la carga elemental
• \( \varepsilon_0 \): la permitividad del vacío
• \( \hbar \): la constante reducida de Planck
• \( c \): la velocidad de la luz

El valor numérico actualizado es:

\[ \alpha \approx \frac{1}{137.035999177} \]

Lo más llamativo de α es que no depende de ningún sistema de unidades. Es un número puro, un parámetro universal que aparece una y otra vez en la física de partículas, la estructura atómica y la interacción entre luz y materia.

Nota. A comienzos del siglo XX, los espectroscopistas esperaban que cada transición electrónica generara una única línea espectral limpia. Sin embargo, muchas líneas aparecían divididas en varios componentes muy cercanos. Este desdoblamiento, conocido como estructura fina, fue explicado por Arnold Sommerfeld en 1916 mediante la incorporación de correcciones relativistas al modelo de Bohr. Para describir cuantitativamente estos desplazamientos energéticos introdujo la constante $ \alpha $.

En el modelo original de Bohr para el hidrógeno, $ \alpha $ equivale, aproximadamente, a la razón entre la velocidad del electrón en el estado fundamental y la velocidad de la luz. 

Por qué α es tan importante

α desempeña un papel esencial en la estructura misma de la materia. Controla la fuerza con la que los electrones son atraídos hacia los núcleos y, por tanto, determina el tamaño de los átomos y la energía de los enlaces químicos. Influye en la química en general y también en los procesos que sustentan la vida dentro de las estrellas.

En electrodinámica cuántica (QED), $ \alpha $ es la constante de acoplamiento electromagnético y mide la intensidad de la interacción entre electrones y fotones.

¿Qué pasaría si $ \alpha $ fuese mayor?

Si \( \alpha \) aumentara, por ejemplo hasta \( 1/110 \), la atracción electromagnética entre electrones y núcleos se volvería más fuerte. Los electrones caerían en órbitas más estrechas y los átomos serían más pequeños.

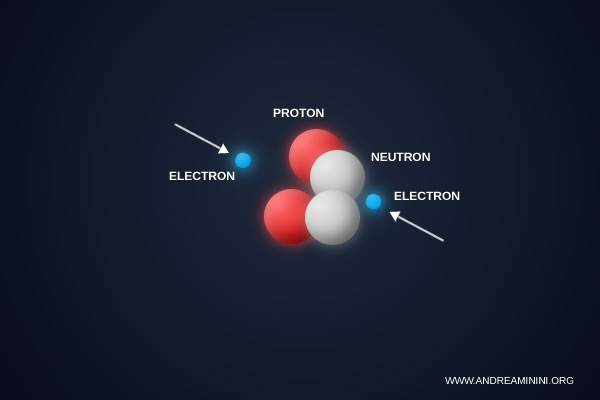
Los enlaces químicos serían más rígidos y difíciles de romper. Esta mayor estabilidad, paradójicamente, impediría la mayoría de las reacciones químicas. Muchos núcleos también se volverían inestables debido al aumento de la repulsión entre protones, de modo que numerosos elementos ni siquiera llegarían a formarse.

Ejemplo. Si los enlaces químicos fueran demasiado fuertes, las moléculas no podrían reorganizarse. La química orgánica se paralizaría y los procesos biológicos dejarían de funcionar. La vida, tal como la conocemos, no sería posible.

¿Y si $ \alpha $ fuese menor?

Si \( \alpha \) disminuyera, digamos hasta \( 1/200 \), la atracción entre electrones y núcleos sería más débil. Los átomos aumentarían de tamaño y serían mucho menos estables.

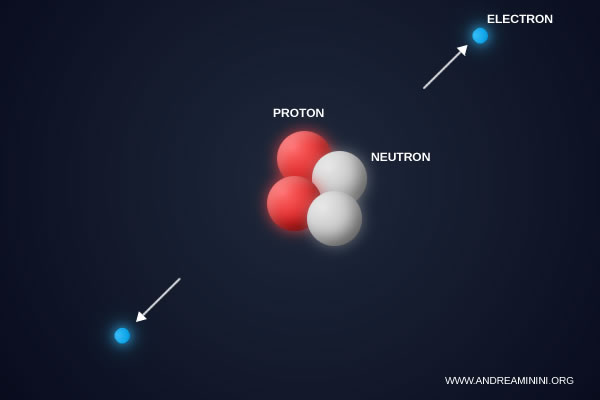
Los enlaces químicos se volverían extremadamente frágiles y la mayoría de las moléculas se descompondría fácilmente. La química orgánica, tal como la conocemos, dejaría de ser posible.

Ejemplo. Moléculas esenciales como el ADN, las proteínas o incluso el agua no podrían mantenerse unidas. Además, las estrellas no podrían sintetizar carbono ni oxígeno. Procesos clave como el triple alfa dependen de resonancias muy ajustadas que cambiarían en cuanto α se desviara de su valor actual.

α y la interacción entre electrones y fotones

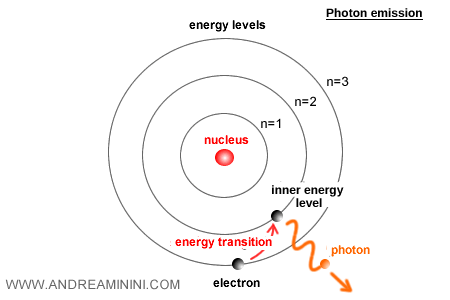
En mecánica cuántica, los electrones no interactúan de forma continua con la luz. En su lugar, intercambian energía mediante eventos discretos: absorben o emiten fotones.

La probabilidad de que ocurra uno de estos eventos depende directamente de \( \alpha \ ). Cuanto mayor es α, más fácilmente un electrón puede absorber o emitir un fotón.

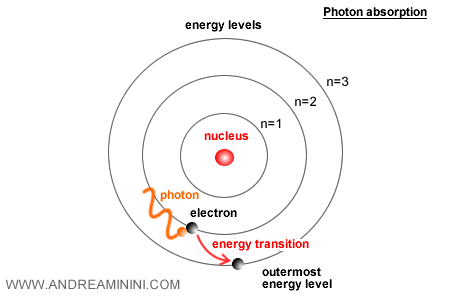
Una α demasiado grande haría que las transiciones electrónicas fuesen demasiado frecuentes. Una α demasiado pequeña las haría prácticamente inexistentes. El valor real, 1/137, proporciona un equilibrio que permite los espectros atómicos observados y al mismo tiempo asegura la estabilidad de los átomos.

Notas adicionales

• Cambio de $ \alpha $ con la energía
  Aunque se le llama "constante", en QED su valor varía con la energía de la interacción, un fenómeno conocido como running. A bajas energías vale aproximadamente $$ \alpha \approx \frac{1}{137} $$ mientras que en colisiones de muy alta energía puede aumentar hasta $$ \alpha \approx \frac{1}{127} $$ debido a los efectos de polarización del vacío.
• La hipótesis del multiverso
  Algunas teorías proponen que existen muchos universos con valores distintos de las constantes fundamentales. En ese contexto, el nuestro sería uno de los pocos donde α adopta un valor compatible con la existencia de materia estable. Aun así, el multiverso es una idea especulativa que no cuenta con verificación experimental.
• El principio antrópico
  Según esta perspectiva, observamos α = 1/137 porque solo universos con un valor semejante pueden albergar observadores capaces de medirlo.

  Nota. El principio antrópico no explica por qué α tiene este valor concreto. Simplemente indica que la existencia de observadores limita el tipo de universo en el que puede aparecer.

• α como referencia universal
  Como $ \alpha = \frac{1}{137} $ es un número puro y parece constante en todo el universo observable, cualquier civilización avanzada obtendría el mismo valor. En ese sentido, α funciona como un punto de referencia común inscrito en las leyes de la física.
  
• ¿Cambia $ \alpha $ con el tiempo o el espacio?
  La mayoría de mediciones actuales indican que $ \alpha $ lleva miles de millones de años con un valor muy estable. En 1999 se informó de una posible discrepancia en la luz de cuásares lejanos, de magnitud $$ \frac{\Delta \alpha}{\alpha} = (-5.7 \pm 1.0) \times 10^{-6} $$ pero los estudios posteriores no confirmaron ese resultado. Hoy por hoy no existe evidencia definitiva ni de variación ni de invariabilidad absoluta.

Y esta historia continúa, porque entender $ \alpha $ es explorar uno de los pilares más profundos de la física moderna.