Momento angular de las partículas
En mecánica cuántica, el momento angular de una partícula describe cómo su estado cuántico responde a las rotaciones en el espacio. Dicho de forma sencilla, explica cómo la función de onda conserva determinadas simetrías cuando el sistema gira.
Este concepto es esencial para comprender el comportamiento de los electrones en los átomos, la estructura de los espectros y muchas propiedades magnéticas. Existen dos formas principales de momento angular:
- Momento angular orbital \( L \)
Está ligado a la dependencia espacial de la función de onda. No representa una órbita real como la de un planeta, sino la simetría de la distribución de probabilidad de la partícula. La cuantización de \( L \) refleja la manera en que la función de onda se organiza en el espacio tridimensional. - Momento angular intrínseco (spin) \( S \)
Es una propiedad interna de la partícula que no corresponde a una rotación física. El spin es un tipo de momento angular puramente cuántico, descrito mediante transformaciones SU(2) y sin un equivalente clásico.
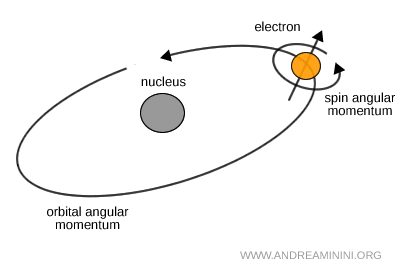
Nota. Es frecuente imaginar el spin como si la partícula girase sobre sí misma. Sin embargo, no se trata de un movimiento real, sino de una propiedad cuántica intrínseca sin representación clásica exacta. Aun así, produce efectos físicos medibles, como momentos magnéticos o desdoblamientos en los niveles de energía. En cambio, el momento angular orbital \( L \) sí está vinculado a la geometría del espacio.
Momento angular en física cuántica
En mecánica clásica, el momento angular se expresa como \( \vec{L} = \vec{r} \times m\vec{v} \). A partir de esta definición, puede descomponerse sin dificultad en tres componentes cartesianas:
$$ \vec{L} = (L_x,\,L_y,\,L_z) $$
Cada componente corresponde a la proyección del vector sobre los ejes \( x \), \( y \) y \( z \).
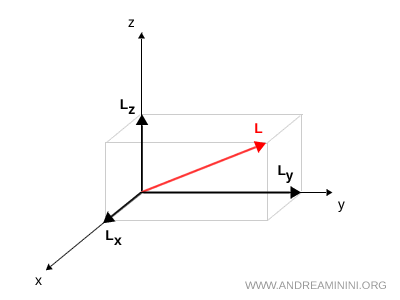
En mecánica cuántica, sin embargo, surge una diferencia fundamental. No es posible medir simultáneamente todas las componentes del momento angular. Si se mide \( L_x \), las componentes \( L_y \) y \( L_z \) quedan inevitablemente afectadas. Por ello, no se pueden determinar con precisión todas las componentes al mismo tiempo.
En los experimentos se mide una única proyección, y por convenio se utiliza el eje \( z \). De este modo, la componente observable es \( L_z \). Además de \( L_z \), puede determinarse el módulo del momento angular:
$$ L = \sqrt{l(l+1)}\,\hbar $$
El número cuántico \( l \) toma valores enteros no negativos \( l = 0, 1, 2, 3, \dots \). La constante \( \hbar \), llamada constante reducida de Planck, fija la escala característica de los fenómenos cuánticos.
Nota. La constante \( \hbar \) se define como $$ \hbar = \frac{h}{2\pi} $$ donde \( h \) es la constante de Planck. Su valor aproximado es $$ \hbar \approx 1.054 \times 10^{-34} , \text{J·s} $$ y aparece en todas las ecuaciones fundamentales de la teoría cuántica.
La expresión \( L = \sqrt{l(l+1)}\,\hbar \) muestra que el momento angular está cuantizado: el valor de \( |\vec{L}| \) no cambia de forma continua, sino en saltos discretos determinados por \( l \).
| \(l\) | \(|\vec{L}|=\sqrt{l(l+1)}\,\hbar\) | Value |
|---|---|---|
| 0 | \(\sqrt{0\cdot 1}\,\hbar\) | \(0\) |
| 1 | \(\sqrt{1\cdot 2}\,\hbar\) | \(\sqrt{2}\,\hbar\) |
| 2 | \(\sqrt{2\cdot 3}\,\hbar\) | \(\sqrt{6}\,\hbar\) |
| 3 | \(\sqrt{3\cdot 4}\,\hbar\) | \(\sqrt{12}\,\hbar\) |
| 4 | \(\sqrt{4\cdot 5}\,\hbar\) | \(\sqrt{20}\,\hbar\) |
| 5 | \(\sqrt{5\cdot 6}\,\hbar\) | \(\sqrt{30}\,\hbar\) |
En muchos problemas resulta conveniente utilizar la magnitud al cuadrado \( L^2 \), ya que simplifica los desarrollos algebraicos:
$$ L^2 = l(l+1)\hbar^2 $$
| \(l\) | \(L^2 = l(l+1)\hbar^2\) | Value |
|---|---|---|
| 0 | \(0\cdot 1\,\hbar^2\) | \(0\,\hbar^2\) |
| 1 | \(1\cdot 2\,\hbar^2\) | \(2\,\hbar^2\) |
| 2 | \(2\cdot 3\,\hbar^2\) | \(6\,\hbar^2\) |
| 3 | \(3\cdot 4\,\hbar^2\) | \(12\,\hbar^2\) |
| 4 | \(4\cdot 5\,\hbar^2\) | \(20\,\hbar^2\) |
| 5 | \(5\cdot 6\,\hbar^2\) | \(30\,\hbar^2\) |
En mecánica cuántica, el operador \( \hat{L}^2 \) posee valores propios bien definidos. Por ello, en muchos problemas resulta más cómodo trabajar con \( L^2 \) que con el módulo \( |\vec{L}| \), especialmente cuando se analizan estados estacionarios.
Nota. Esta cuantización no existe en la física clásica, donde el módulo del momento angular puede adoptar cualquier valor real sin restricción.
La proyección del momento angular orbital sobre el eje \( z \) también está cuantizada y viene dada por
$$ L_z = m_l \hbar $$
Aquí \( m_l \) es el número cuántico magnético, cuyos valores permitidos son enteros entre \( -l \) y \( l \):
$$ m_l = -l, -l+1, \dots, -1, 0, +1, \dots, l-1, l $$
La tabla siguiente resume los valores posibles de \( m_l \) y sus correspondientes proyecciones \( L_z \).
| \(l\) | Valores permitidos de \(m_l\) | Valores correspondientes de \(L_z\) | Número de estados \((2l+1)\) |
|---|---|---|---|
| 0 | \(0\) | \(0\) | 1 |
| 1 | \(-1,\,0,\,+1\) | \(-\hbar,\,0,\,+\hbar\) | 3 |
| 2 | \(-2,\,-1,\,0,\,+1,\,+2\) | \(-2\hbar,\,-\hbar,\,0,\,+\hbar,\,+2\hbar\) | 5 |
| 3 | \(-3,\,-2,\,-1,\,0,\,+1,\,+2,\,+3\) | \(-3\hbar,\,-2\hbar,\,-\hbar,\,0,\,+\hbar,\,+2\hbar,\,+3\hbar\) | 7 |
Por ejemplo, si \( l = 2 \), la proyección de \( \vec{L} \) sobre el eje \( z \) solo puede tomar cinco valores: \(-2\hbar, -\hbar, 0, +\hbar, +2\hbar\).
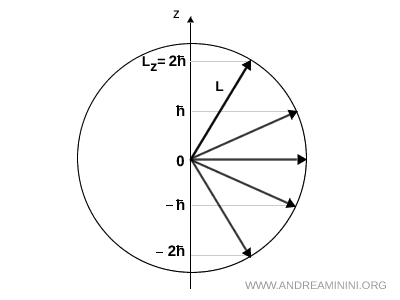
En este caso, el módulo del momento angular está fijado por \( |\vec{L}| = \sqrt{l(l+1)}\,\hbar \), de modo que todos los vectores tienen la misma longitud y se distribuyen sobre la superficie de una esfera. La proyección \( L_z \), sin embargo, solo puede tomar los valores discretos \( L_z = m_l \hbar \).
Las cinco flechas de la figura representan las orientaciones permitidas de \( \vec{L} \) para \( l = 2 \). Todas poseen el mismo módulo, pero forman ángulos distintos con el eje \( z \), tal como impone la condición \( L_z = m_l \hbar \).
Nota. Incluso cuando \( m_l = l \), el vector \( \vec{L} \) no puede alinearse exactamente con el eje \( z \). Si lo hiciera, se tendría \( |\vec{L}| = |L_z| \), pero en realidad \( |\vec{L}| = \sqrt{l(l+1)}\,\hbar > l\hbar = L_z^{\text{máx}} \). Esto obliga a que \( \vec{L} \) conserve componentes en otras direcciones, dando lugar a su movimiento de precesión.
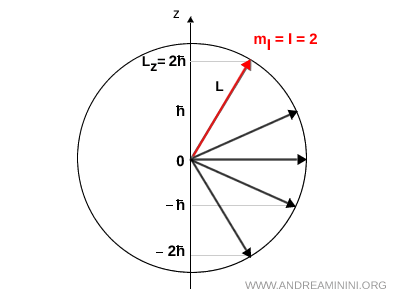
Es importante recordar que \( L_z \) es una componente vectorial orientada. Por ello puede ser positiva, negativa o nula. Un módulo, en cambio, es siempre positivo. Esta diferencia es fundamental para interpretar correctamente el significado físico de \( L_z \).
Momento Angular de Spin
El spin es el momento angular intrínseco de una partícula. Se trata de una propiedad esencial de la materia a escala cuántica y desempeña un papel clave en la estructura de los átomos, el magnetismo y la física de partículas.
A diferencia del momento angular orbital, el spin no proviene de un movimiento en el espacio. Es una característica fundamental, tan básica como la masa o la carga eléctrica. Sin embargo, su comportamiento matemático sigue las mismas reglas que cualquier otro momento angular cuántico.
El módulo del vector de spin está cuantizado y viene dado por la expresión
$$ S = \sqrt{ s(s+1) } \hbar $$
o, de forma equivalente, por su valor al cuadrado
$$ S^2 = s(s+1) \hbar^2 $$
El número cuántico de spin \( s \) puede adoptar valores enteros o semienteros:
$$ s = 0, \tfrac12, 1, \tfrac32, 2, \tfrac52, \ldots $$
Del mismo modo, la proyección del spin sobre un eje concreto, normalmente el eje z, también está cuantizada:
$$ S_z = m_s \hbar $$
El número cuántico magnético \( m_s \) puede tomar los valores \( m_s = -s, -s+1, \ldots, s-1, s \), dando lugar a \( 2s+1 \) estados posibles.
En el caso del electrón, donde \( s = \tfrac12 \), existen dos configuraciones: \( m_s = +\tfrac12 \), conocido como estado spin up, y \( m_s = -\tfrac12 \), conocido como spin down.
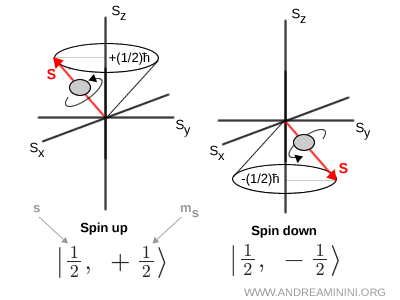
En el lenguaje habitual de la mecánica cuántica, estos estados se escriben mediante notación bra-ket: \( | s,\ m_s \rangle \). Así, \( \left| \tfrac12,\ +\tfrac12 \right\rangle \) representa el estado spin up y \( \left| \tfrac12,\ -\tfrac12 \right\rangle \) el estado spin down.
Nota. Aunque el spin no procede de un movimiento físico en el espacio, comparte con el momento angular orbital el hecho de tener un valor total cuantizado y una única componente medible a lo largo de un eje de referencia.
Valores típicos del spin
A modo de referencia, la siguiente tabla resume algunos valores de \( s \), junto con sus posibles proyecciones \( m_s \) y los valores correspondientes de \( S_z \).
| \( s \) | \( S^2 = s(s+1)\hbar^2 \) | Valores de \( m_s \) | Valores de \( S_z \) | Estados posibles \( 2s+1 \) |
|---|---|---|---|---|
| \( \tfrac12 \) | \( \tfrac34 \hbar^2 \) | \( -\tfrac12, +\tfrac12 \) | \( -\tfrac12\hbar, +\tfrac12\hbar \) | 2 |
| \( 1 \) | \( 2\hbar^2 \) | \( -1, 0, +1 \) | \( -\hbar, 0, +\hbar \) | 3 |
| \( \tfrac32 \) | \( \tfrac{15}{4}\hbar^2 \) | \( -\tfrac32, -\tfrac12, +\tfrac12, +\tfrac32 \) | \( -\tfrac32\hbar, -\tfrac12\hbar, +\tfrac12\hbar, +\tfrac32\hbar \) | 4 |
Un rasgo verdaderamente intrínseco
A diferencia del momento angular orbital, el spin es una propiedad fija. Una partícula puede encontrarse en diferentes estados orbitales, pero su valor de \( s \) no cambia. Por ejemplo, el protón, el neutrón y el electrón tienen siempre \( s = \tfrac{1}{2} \), mientras que el fotón y el gluón tienen \( s = 1 \).
| Bosones (spin entero) | Fermiones (spin semientero) | ||
|---|---|---|---|
| Spin 0 | Spin 1 | Spin \( \tfrac{1}{2} \) | Spin \( \tfrac{3}{2} \) |
| Mesones pseudosescalares $ \pi, K, \eta, \eta' $ |
Fotones ( \( \gamma \) ) Gluones ( \( g \) ) Bosones \( W^+, W^-, Z \) Mesones vectoriales $ \rho, \omega, \phi, K^*, J/\psi, \Upsilon $ |
Quarks, leptones protones ( \( p \) ), neutrones ( \( n \) ) electrones ( \( e \) ) Octete bariónico $ p,\ n , \Sigma^{+},\ \Sigma^{0},\ \Sigma^{-} $ $ \Xi^{0},\ \Xi^{-} , \Lambda^{0} $ |
Decuplete bariónico $ \Delta^{++},\ \Delta^{+},\ \Delta^{0},\ \Delta^{-} $ $ \Sigma^{*+},\ \Sigma^{*0},\ \Sigma^{*-} $ $ \Xi^{*0},\ \Xi^{*-} $ $ \Omega^{-} $ |
En resumen, las partículas con spin entero se denominan bosones y siguen la estadística de Bose-Einstein, mientras que las de spin semientero se conocen como fermiones y cumplen el principio de exclusión de Pauli.
Nota avanzada. En los fermiones, los autoestados de spin sólo recuperan exactamente su configuración inicial tras una rotación de \( 4\pi \). Este comportamiento, sin análogo clásico, revela la auténtica naturaleza cuántica del spin.
Un ejemplo práctico
Consideremos ahora un electrón en un orbital (p), caracterizado por el número cuántico orbital
$$ l = 1 $$
En un orbital (p) intervienen dos contribuciones independientes al momento angular total:
- \( L \), que describe la simetría espacial de la función de onda y determina la forma del orbital
- \( S \), que define el estado de spin y no modifica la geometría orbital
Analicemos ambas por separado.
1) Momento angular orbital \( \mathbf{L} \)
Para \( l = 1 \) se obtiene:
$$ L^2 = l(l+1)\hbar^2 = 2\hbar^2 $$
$$ |\mathbf{L}| = \sqrt{2}\,\hbar $$
donde \( \hbar \) es la constante reducida de Planck.
Los orbitales (p), con su forma característica de dos lóbulos, se describen mediante los armónicos esféricos
$$ Y_1^{-1},\; Y_1^{0},\; Y_1^{+1} $$
correspondientes a los valores permitidos
$$ m_l = -1,\; 0,\; +1 $$
Desde el punto de vista físico, \( \mathbf{L} \) no apunta en una dirección fija: precesa describiendo un cono alrededor del eje \( z \).
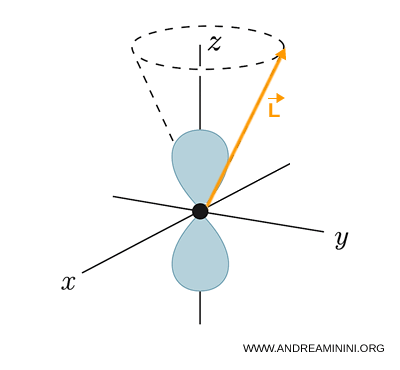
La forma de los orbitales (p) es, de hecho, la manifestación directa de que \( l = 1 \).
2) Momento angular de spin \( \mathbf{S} \)
El electrón posee además spin:
$$ s = \frac{1}{2} $$
con valores permitidos
$$ m_s = \pm \frac{1}{2} $$
Por tanto, para cada orbital (p) existen dos posibles estados de spin:
- (p) con \( m_s = +\tfrac{1}{2} \)
- (p) con \( m_s = -\tfrac{1}{2} \)
El spin no representa una rotación física del electrón en el espacio. Es una propiedad interna e independiente de la geometría orbital.
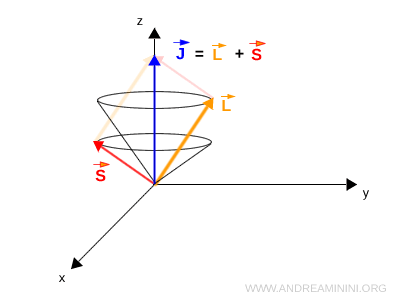
En conjunto, un mismo estado cuántico contiene dos aportes al momento angular: el orbital \( L \) y el de spin \( S \). Su suma vectorial define el momento angular total:
$$ \mathbf{J} = \mathbf{L} + \mathbf{S} $$
Este acoplamiento produce desdoblamientos característicos en los niveles de energía, visibles en los espectros atómicos como estructura fina.
¿Qué representan los conos del diagrama? Los vectores no permanecen estáticos: describen un movimiento de precesión. En particular, \( L \) y \( S \) precesan alrededor de \( J \), y \( J \) lo hace alrededor de la dirección del campo magnético externo. Esta dinámica genera las superficies cónicas que aparecen en la ilustración.
Combinación de momentos angulares cuánticos
En física clásica, sumar dos momentos angulares es un proceso sencillo. Se suman las componentes de los vectores y el resultado queda perfectamente determinado. Pero en mecánica cuántica las reglas cambian por completo.
Las componentes del operador de momento angular no conmutan entre sí. Esto significa que no podemos conocer simultáneamente sus tres componentes, lo que vuelve la combinación de dos momentos angulares en un problema mucho más sutil.
La pregunta clave es esta: cómo combinar dos momentos angulares cuando no es posible fijar al mismo tiempo las componentes de cada uno.
En un sistema cuántico solo dos magnitudes quedan bien definidas para un momento angular:
- la componente en la dirección z, dada por el autovalor \( m \) de \( J_z \)
- el momento angular total, descrito por el número cuántico \( j \) asociado a \( J^2 \)
En este contexto, la imagen clásica de un vector con una orientación espacial concreta deja de tener sentido. Por eso la suma vectorial ordinaria no funciona aquí.
Hay una regla que sí se mantiene sin excepciones: las componentes en z se suman tal cual:
$$ m = m_1 + m_2 $$
Sin embargo, determinar el valor total del momento angular es más complicado. Su magnitud no está fijada, y eso se debe a que la orientación relativa de los dos momentos angulares no es un observable en el sentido cuántico. En ocasiones pueden comportarse como si estuvieran más o menos alineados, pero esa "orientación" no puede medirse ni definirse de manera clásica.
El resultado es que el momento angular total no adopta un único valor. En cambio, puede situarse en un conjunto discreto de valores permitidos, que van desde un mínimo hasta un máximo:
$$ j = \lvert j_1 - j_2 \rvert,\ \lvert j_1 - j_2 \rvert + 1,\ \ldots,\ ( j_1 + j_2 ) - 1,\ (j_1 + j_2) $$
Si los momentos angulares se comportaran como paralelos, obtendríamos \( j_1 + j_2 \). Si actuaran como antiparalelos, obtendríamos \( |j_1 - j_2| \). Todos los valores intermedios forman una secuencia cuantizada igualmente espaciada.
$$ j = \lvert j_1 - j_2 \rvert,\ \underbrace{\lvert j_1 - j_2 \rvert + 1,\ \ldots,\ ( j_1 + j_2 ) - 1}_{valor\ cuantizado},\ (j_1 + j_2) $$
Esto refleja un aspecto fundamental de la mecánica cuántica: los autovalores de \( J^2 \) están cuantizados. Por eso el momento angular total solo puede tomar valores enteros o semienteros, como \( j = 0, \frac{1}{2}, 1, \frac{3}{2}, 2, ... \). Valores intermedios son simplemente imposibles debido a la estructura algebraica del operador.
Ejemplo. Imaginemos una partícula con espín 1 en un estado orbital con momento angular \( l = 3 \). Debemos combinar:
- el momento angular orbital \( j_1 = 3 \)
- el momento angular de espín \( j_2 = 1 \)
Si ambos momentos angulares se comportaran como paralelos, obtendríamos \( j = 4 \). Si actuaran como antiparalelos, el valor sería \( j = 2 \). Por tanto los valores posibles van de 2 a 4. Dado que solo se permiten valores discretos, el momento angular total puede tomar tres valores: $$ j = 2, 3, 4 $$ Esto implica que la partícula puede combinar su momento angular orbital y su espín de tres maneras diferentes, cada una ligada a un nivel energético distinto y, en consecuencia, a un estado físico diferenciado.
En definitiva, al sumar dos momentos angulares cuánticos no obtenemos un único valor, sino un pequeño espectro de opciones permitidas. Las componentes en z se suman como de costumbre, pero el momento angular total queda restringido a los valores cuantizados comprendidos entre un mínimo y un máximo.