Electrodinámica Cuántica

Electrodinámica Cuántica (QED, por sus siglas en inglés) es la teoría cuántica de campos que describe cómo las partículas cargadas (como electrones, positrones y quarks) interactúan entre sí mediante el intercambio de fotones.

Se la considera la más antigua, sencilla y a la vez la más precisa y exitosa de todas las teorías cuánticas de campos.

La QED surgió como una extensión de la teoría clásica del electromagnetismo de Maxwell, adaptándola a la mecánica cuántica y a la relatividad especial. Además, sentó las bases para teorías fundamentales posteriores, como la cromodinámica cuántica y la teoría electrodébil.

Fue formulada y perfeccionada en la década de 1940 por Tomonaga, Feynman y Schwinger.

¿Por qué es importante? La QED es de una precisión extraordinaria: sus predicciones coinciden con los resultados experimentales hasta en 12 cifras decimales. Introdujo, además, herramientas centrales de la física moderna, como los diagramas de Feynman y el concepto de partículas virtuales. De manera más amplia, se convirtió en el modelo de referencia de todas las teorías gauge, incluido el propio Modelo Estándar.

Cómo funciona, en pocas palabras

La QED interpreta toda interacción electromagnética como un intercambio de fotones entre partículas cargadas.

En otras palabras, las partículas cargadas no actúan nunca de manera directa unas sobre otras.

La interacción se produce a través del intercambio de fotones virtuales, que aparecen como líneas internas en los diagramas de Feynman.

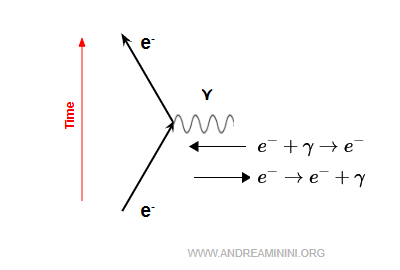
Un electrón puede:

• emitir un fotón virtual  $$ e^- \;\rightarrow\; e^- + \gamma $$
• absorber un fotón virtual  $$ e^- + \gamma \;\rightarrow\; e^- $$

Nota. Los fotones reales son partículas observables (como la luz visible). Los fotones virtuales, en cambio, no son partículas libres: no pueden detectarse directamente, sino que actúan como intermediarios que transmiten la interacción.

En la física clásica, dos electrones se repelen porque tienen la misma carga eléctrica (repulsión de Coulomb).

En la QED, esa repulsión se entiende como un intercambio continuo de fotones virtuales entre ambos electrones.

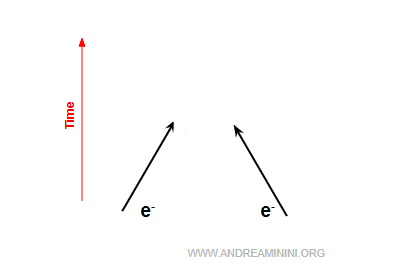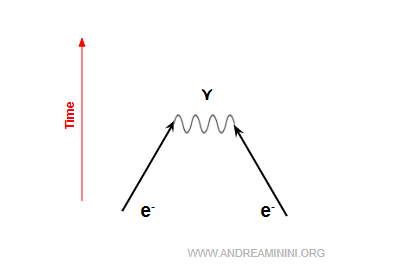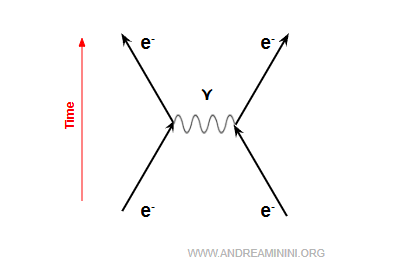
Estos fotones virtuales transportan cantidad de movimiento, y el intercambio desvía las trayectorias de los electrones, obligándolos a separarse.

Este proceso en QED se conoce como dispersión de Møller, al involucrar a dos electrones.

$$ e^- + e^- \rightarrow e^- + e^- $$

Así, cada vez que dos partículas cargadas “se perciben” a distancia, no se trata de una acción instantánea a distancia (como en la física clásica), sino del resultado de un intercambio cuántico de fotones virtuales.

Nota. Si dos partículas tienen cargas del mismo signo, el intercambio de fotones virtuales produce repulsión. Si las cargas son opuestas, el intercambio genera atracción. Los fotones virtuales son, por tanto, los portadores de la interacción electromagnética, capaces de mediar tanto repulsión como atracción, según el tipo de carga. Conviene subrayarlo, pues a menudo se asume erróneamente que “solo transmiten repulsión”.

Ejemplos

Estos son algunos de los procesos más representativos descritos por la QED:

1] Dispersión de Compton

Un electrón colisiona con un fotón real y lo dispersa.

$$ e^- + \gamma \;\longrightarrow\; e^- + \gamma $$

En este proceso, un fotón impacta contra un electrón y emerge con una longitud de onda distinta (efecto Compton).

Constituyó una de las pruebas más claras de la naturaleza corpuscular de la luz.

Así se representa en un diagrama de Feynman, con el tiempo ascendiendo en el gráfico.

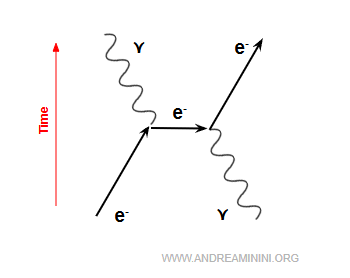
2] Aniquilación

En este proceso, un electrón ($e^-$) y un positrón ($e^+$, su antipartícula) se encuentran y convierten su masa en energía en forma de fotones.

$$ e^- + e^+ \;\;\longrightarrow\;\; \gamma + \gamma $$

La conservación de energía y momento exige al menos dos fotones en el estado final, emitidos en direcciones opuestas.

Como los fotones son sus propias antipartículas, la producción de dos asegura que se respeten todas las leyes de conservación.

Así aparece la aniquilación electrón-positrón en un diagrama de Feynman.

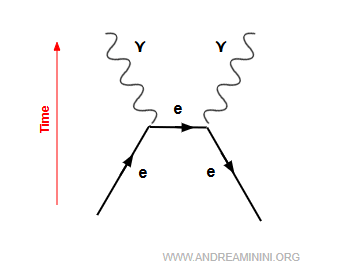
La flecha que apunta en sentido contrario al tiempo representa la antipartícula del electrón: el positrón.

En esencia, la aniquilación electrón-positrón es el proceso inverso a la producción de pares ($\gamma + \gamma \to e^- + e^+$).

3] Producción de pares

Es el proceso inverso a la aniquilación: un fotón de alta energía se transforma en un par partícula-antipartícula, normalmente un electrón y un positrón:

$$ \gamma + \gamma  \;\;\longrightarrow\;\; e^- + e^+ $$

Dos fotones se convierten en un par electrón-positrón.

En otras palabras, la producción de pares es la conversión de energía lumínica en materia (una partícula y su antipartícula).

 

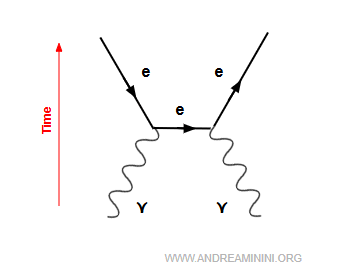
Es el inverso de la aniquilación y una demostración notable de la equivalencia masa-energía, $E = mc^2$.

Nota. Este proceso no puede ocurrir en el vacío: un único fotón no puede transformarse en un par por sí solo, ya que eso violaría la conservación del momento. Es necesario un núcleo cercano (o, en casos menos frecuentes, otro electrón) que actúe como “blanco” y absorba parte del momento. El proceso real es, por tanto: $$ \gamma + N \;\; \longrightarrow\;\; e^- + e^+ + N $$ donde $N$ es el núcleo, que permanece prácticamente inalterado. Por ejemplo, un fotón gamma que incide en un átomo pesado puede dar lugar a un par $e^- + e^+$.

4] Dispersión de Bhabha

Es la dispersión elástica entre un electrón y un positrón.

$$ e^- + e^+ \;\;\longrightarrow\;\; e^- + e^+ $$

Lleva el nombre del físico indio Homi Jehangir Bhabha, quien en 1935 fue el primero en calcular su sección eficaz en el marco de la QED.

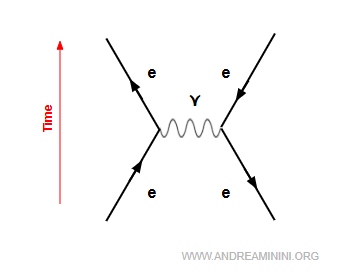
Un electrón y un positrón se aniquilan en un fotón virtual.

$$ e^+ + e^- \rightarrow \gamma + \gamma $$

Casi de inmediato, el fotón genera un nuevo par electrón-positrón $e^- + e^+$.

$$ \gamma + \gamma \rightarrow e^+ + e^- $$

En otras palabras, entran un electrón y un positrón, y salen un electrón y un positrón. No son los mismos, desde luego, pero dado que los electrones son indistinguibles por naturaleza, no supone diferencia práctica alguna.

Nota. Un fotón que aparece como línea interna en un diagrama de Feynman es una partícula virtual, no sujeta a la relación de dispersión habitual $ E = pc $. Puede transportar energía y momento arbitrarios, lo que lo sitúa “fuera de la capa de masa” (off-shell). Por ello, el diagrama puede mostrar legítimamente un único fotón virtual sin violar las leyes de conservación en ese vértice. En cambio, en el proceso físico, toda aniquilación electrón-positrón debe producir siempre dos fotones reales para conservar simultáneamente la energía y el momento. Las líneas externas del diagrama representan estas partículas reales, como en la dispersión de Bhabha, donde el estado final vuelve a ser un par electrón-positrón.

¿Cuál es la diferencia entre fotones reales y virtuales?

En la QED es crucial distinguir con precisión entre fotones reales y fotones virtuales.

• Fotones reales
  Un fotón real es un cuanto observable del campo electromagnético. Se propaga libremente por el espacio a la velocidad de la luz y satisface de manera estricta la relación energía-momento; en otras palabras, está “en la capa de masa” (on-shell): $$ E^2 = (pc)^2 + (mc^2)^2 \quad \;\; \text{con } m=0 \;\Rightarrow\; E = pc $$ Los fotones reales son los cuantos que podemos detectar directamente: luz visible, rayos X o radiación gamma.

  Ejemplos: la luz solar que llega a la Tierra, el haz coherente de un láser o un fotón gamma emitido en un decaimiento nuclear. En la práctica, los fotones reales constituyen la radiación electromagnética que podemos medir con nuestros instrumentos.

• Fotones virtuales
  Los fotones virtuales, en cambio, son los “mediadores ocultos” de las interacciones electromagnéticas. El intercambio de estos fotones es lo que genera fuerzas como la atracción o la repulsión de Coulomb entre cargas. Pero un fotón virtual no es una partícula detectable por sí misma: aparece únicamente como línea interna en los diagramas de Feynman, representando estados intermedios de la interacción. A diferencia de los reales, no está limitado por la relación $E = pc$. Puede transportar combinaciones de energía y momento imposibles para un fotón libre, y por eso se dice que está fuera de la capa de masa (off-shell). En este sentido, “fotón virtual” es más bien una convención conceptual propia del formalismo de los diagramas de Feynman que la descripción de una partícula física en el sentido usual.

  Nota. A menudo se afirma que los fotones virtuales “solo existen por un instante” gracias al principio de incertidumbre de Heisenberg: $$ \Delta E \, \Delta t \gtrsim \hbar $$ La idea es que un sistema puede “tomar prestada” una energía $\Delta E$ siempre que la “devuelva” en un tiempo suficientemente corto $\Delta t$. Cuanto mayor sea la discrepancia energética, más breve es el lapso permitido. Esta imagen heurística puede ser útil para la intuición, pero en la QED rigurosa los fotones virtuales no poseen existencia autónoma: son únicamente términos matemáticos que aparecen en los cálculos perturbativos. La energía y el momento se conservan exactamente en cada vértice de interacción; lo único que no se exige entre vértices es la condición de ser un fotón libre y on-shell.

Pantalla cuántica en la QED

En la electrodinámica cuántica, el vacío no es un espacio vacío, sino un trasfondo en constante agitación de fluctuaciones cuánticas. Durante intervalos brevísimos, estas fluctuaciones pueden dar lugar a pares virtuales electrón-positrón, representados en los diagramas de Feynman como un bucle de fermiones unido a una línea de fotón virtual. 

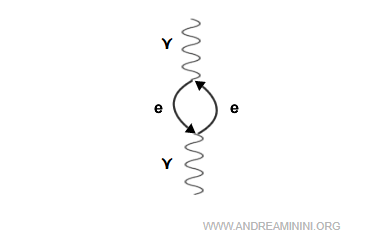
De esta manera, el vacío se comporta de forma análoga a un medio dieléctrico. A este efecto se le denomina polarización del vacío.

Una carga eléctrica real (por ejemplo, un electrón) interactúa de manera continua con estos pares virtuales.

Los positrones virtuales (cargas positivas) son atraídos hacia la carga negativa del electrón, mientras que los electrones virtuales (cargas negativas) son repelidos hacia fuera.

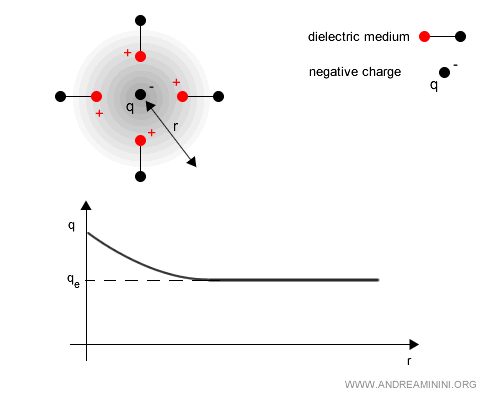
El resultado es una “nube” de carga opuesta alrededor, que atenúa la intensidad del campo eléctrico externo.

A grandes distancias, la carga efectiva $ q_e $ se percibe como menor que la carga desnuda $ q $.

Este fenómeno se conoce como pantalla del vacío.

A distancias muy cortas -o, equivalentemente, a altas energías- se penetra en la nube de polarización y se detecta una carga efectiva mayor.

Por ello, la constante de acoplamiento electrón-fotón $ \alpha $ no es una magnitud fija, sino que depende de la escala de energía: un efecto denominado corrimiento o running de la constante de acoplamiento.

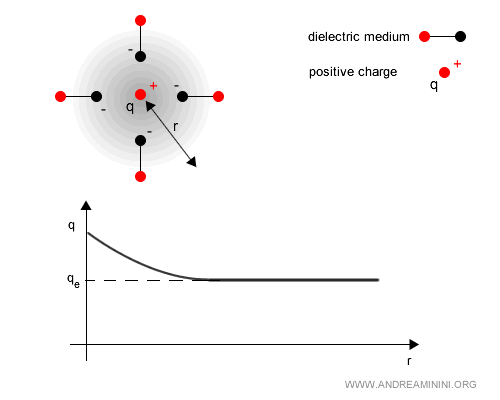
Nota. El mismo mecanismo opera con cargas positivas: los electrones virtuales se concentran en torno a la carga, mientras que los positrones virtuales son expulsados. El resultado sigue siendo la polarización del vacío. 

 

Dado que la carga desnuda está siempre “protegida” por esta pantalla, solo puede hacerse visible a distancias extremadamente cortas. 

La carga que medimos habitualmente con nuestros instrumentos es, en consecuencia, la carga “efectiva”, es decir, la carga tamizada por el vacío.

Y así sucesivamente.