Relatividad Especial
La relatividad especial es una teoría formulada por Albert Einstein en 1905. Amplía la mecánica clásica a los casos en los que los objetos se desplazan a velocidades próximas a la de la luz en el vacío.
En pocas palabras, la relatividad especial transforma nuestra intuición cotidiana sobre el espacio y el tiempo, que la mecánica clásica concebía como magnitudes absolutas e independientes.
Plantea un marco unificado y simétrico del espacio-tiempo, en el que el espacio y el tiempo son relativos y dependen del estado de movimiento del observador.
Los dos postulados fundamentales
La teoría se basa en dos principios comprobados experimentalmente:
- Principio de relatividad
Las leyes de la física son idénticas en todos los sistemas de referencia inerciales, es decir, aquellos que no experimentan aceleración. No existe un sistema privilegiado: las ecuaciones de la física deben conservar la misma forma para cualquier observador que se desplace en línea recta con velocidad constante. - Constancia de la velocidad de la luz
La velocidad de la luz en el vacío tiene siempre el mismo valor para todos los observadores, independientemente del movimiento de la fuente emisora o del propio observador. Esta velocidad es una constante universal: $$ c \approx 3 \times 10^8 \,\text{m/s} $$
En conjunto, estos postulados revolucionan la manera en que entendemos el espacio y el tiempo, que en la mecánica clásica se consideraban fijos y absolutos.
En particular, conducen a fenómenos como la dilatación temporal, la contracción de las longitudes, la relatividad de la simultaneidad y la equivalencia entre masa y energía.
Nota. En 1915, Einstein amplió la relatividad para incluir sistemas acelerados y la gravedad, dando origen a la Relatividad General, en la que el espacio-tiempo se curva debido a la presencia de masa-energía. La relatividad especial (1905) no debe confundirse con la relatividad general (1915). Ambas son teorías de Einstein, pero tratan ámbitos distintos.
Dilatación temporal
La dilatación temporal es el fenómeno por el cual el tiempo medido por un observador externo resulta mayor que el tiempo medido en el sistema en el que ocurre el suceso (el sistema en reposo).
Se trata de una de las consecuencias más sorprendentes de la relatividad especial: el tiempo no transcurre de igual manera para todos los observadores.
Un reloj en movimiento se atrasa con respecto al tiempo registrado por un observador estacionario.
$$ \Delta t = \gamma \cdot \Delta t_0 \quad \text{con} \quad \gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}} $$
Donde:
- $\Delta t_0$ es el tiempo propio, el tiempo medido en el sistema donde el reloj permanece en reposo.
Este tiempo es inherente al fenómeno y se mide en el marco de referencia del suceso observado. - $\Delta t$ es el tiempo dilatado, registrado por un observador que percibe el reloj en movimiento: para él, el reloj marca el tiempo más lentamente que los relojes de su propio sistema.
- $\gamma$ es el factor de Lorentz, siempre mayor que 1 para $v>0$.
A medida que la velocidad relativa se aproxima a la de la luz, la dilatación temporal se acentúa y el tiempo en el sistema en movimiento transcurre cada vez más despacio en comparación con el del observador en reposo.
Por ejemplo, si $t$ es el tiempo medido en la Tierra y observamos una nave que viaja a velocidades cercanas a la de la luz, el tiempo $t'$ a bordo de la nave transcurre mucho más lentamente que el tiempo terrestre.
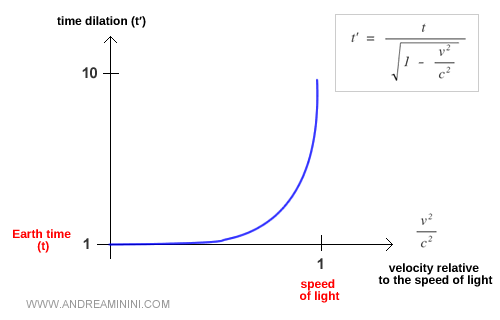
Este efecto está en la base de la famosa paradoja de los gemelos.
Dos gemelos parten de un mismo sistema de referencia (la Tierra). Uno permanece en la Tierra, mientras que el otro viaja al espacio en una nave que se desplaza a velocidad relativista, próxima a la de la luz. Al regresar, los gemelos ya no tienen la misma edad:
- El gemelo que se quedó en la Tierra ha envejecido más.
- El gemelo viajero es más joven.
La explicación está en la dilatación temporal: durante el viaje, el tiempo a bordo de la nave transcurrió más lentamente que el tiempo medido en la Tierra.
La dilatación temporal no es solo una predicción teórica. Ha sido confirmada en numerosas ocasiones de manera inequívoca en experimentos, especialmente en la física de partículas de alta energía.
Por ejemplo, una partícula inestable (como un muón) se mueve a velocidades relativistas. Si su vida media en reposo es $ \Delta t_0 = 2.2 \,\mu s $, entonces, para un observador en la Tierra que lo ve viajar a $v = 0.99 \cdot c$, casi la velocidad de la luz, la vida media observada será $ \Delta t = 15.6 \,\mu s $. $$ \gamma \approx \frac{1}{\sqrt{1 - 0.99^2}} \approx 7.1 $$ $$ \Delta t = 7.1 \cdot 2.2 \approx 15.6 \,\mu s $$ El muón sobrevive más de lo esperado porque, desde su propio marco de referencia, el tiempo transcurre más lentamente.
Contracción de las longitudes
La contracción de las longitudes es el fenómeno por el cual un objeto en movimiento aparece más corto en la dirección de su desplazamiento en comparación con su longitud medida en reposo.
Un objeto en movimiento se observa más corto en la dirección de su movimiento que cuando está en reposo.
$$ L = \frac{L_0}{\gamma} $$
Donde:
- $L_0$ es la longitud propia en el sistema en el que el objeto está en reposo.
- $L$ es la longitud contraída, medida por un observador para quien el objeto está en movimiento.
Por ejemplo, una nave espacial de 100 m de longitud en reposo viaja a $v = 0.8 \cdot c$ con respecto a la Tierra, es decir, al 80% de la velocidad de la luz. En este caso, el factor de Lorentz es 1.667. $$ \gamma = \frac{1}{\sqrt{1 - 0.8^2}} = \frac{1}{\sqrt{0.36}} = \frac{1}{0.6} \approx 1.667 $$ La nave en movimiento, observada desde la Tierra, mide unos 60 metros. $$ L = \frac{100}{1.667} \approx 60 \,\text{m} $$ Así, la nave parece más corta para el observador terrestre.
La relatividad de la simultaneidad
Dos sucesos que son simultáneos en un sistema de referencia pueden no serlo en otro sistema que se mueva con respecto al primero.
La simultaneidad, por tanto, no es absoluta, sino que depende del marco de referencia del observador.
Este efecto se deduce de las transformaciones de Lorentz, que muestran que espacio y tiempo están indisolublemente ligados.
Por ejemplo, un observador en un tren en movimiento ve que dos rayos caen al mismo tiempo en los extremos de un vagón. En cambio, un observador en el suelo no los percibe como simultáneos, ya que la luz recorre distancias distintas debido al movimiento del tren.
Equivalencia masa-energía
La masa y la energía son dos manifestaciones de una misma magnitud física.
Esta equivalencia es la conocida ley de Einstein:
$$ E = mc^2 $$
Donde:
- $E$ es la energía contenida en la masa en reposo $m$.
- $c$ es la velocidad de la luz en el vacío.
Esta relación constituye la base tanto de la generación de energía nuclear como de las armas nucleares.
Por ejemplo, un gramo de masa (0.001 kg) equivale a: $$ E = 0.001 \cdot (3 \times 10^8)^2 = 9 \times 10^{13} \,\text{J} $$ Una cantidad descomunal de energía, equivalente a la explosión de varias decenas de toneladas de TNT.
Y así sucesivamente.