Transformaciones de Lorentz

Las transformaciones de Lorentz explican cómo se modifican las coordenadas espacio-temporales de un acontecimiento al pasar de un sistema de referencia inercial a otro que se desplaza en línea recta con velocidad constante respecto al primero.

Estas transformaciones constituyen la base de la relatividad especial de Einstein, ya que garantizan que las leyes de la física -y, en particular, la velocidad de la luz en el vacío- se mantengan invariables en cualquier sistema inercial.

Su validez se limita exclusivamente a sistemas inerciales dentro del marco de la relatividad.

¿Qué entendemos por sistema inercial?

Un sistema inercial es un sistema de referencia en el que se cumple la primera ley de Newton: un cuerpo libre, si no actúan fuerzas externas sobre él, conserva indefinidamente un movimiento rectilíneo uniforme.

¿Qué plantea la relatividad especial?

La relatividad especial establece que:

• ningún sistema inercial es privilegiado sobre otro
• las leyes de la física deben expresarse con la misma forma en todos los sistemas inerciales, tanto en reposo como en movimiento uniforme
• la velocidad de la luz en el vacío es constante y tiene el mismo valor para todos los observadores

De ello se deduce que la luz no necesita un “medio” estacionario (el éter) para propagarse, y que no existe un punto fijo universal frente al cual se pueda medir un movimiento absoluto.

Las ecuaciones de transformación de Lorentz

Consideremos dos observadores (o sistemas de referencia):

• $S$: el sistema de referencia considerado “en reposo”
• $S'$: el sistema que se mueve con velocidad constante $v$ a lo largo del eje $x$

Para simplificar, supondremos que el movimiento se produce únicamente sobre el eje $x$, de manera que las demás coordenadas espaciales $y$ y $z$ permanecen sin alteración.

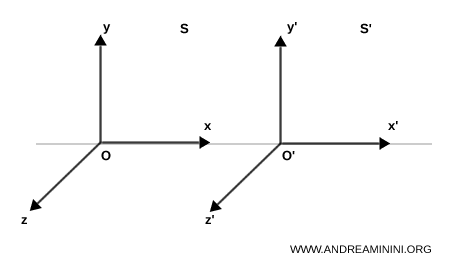
Un acontecimiento que tiene lugar en el sistema $S$ con coordenadas $(x, y, z, t)$ se describirá en el sistema $S'$ con coordenadas $(x', y', z', t')$, de acuerdo con las transformaciones de Lorentz:

$$
\begin{cases}
x' &= \gamma (x - vt) \\
y' &= y \\
z' &= z \\
t' &= \gamma \left(t - \frac{v}{c^2} x\right)
\end{cases}
$$

Aquí, el factor de Lorentz $ \gamma $ se define como:

$$ \gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}} $$

Obsérvese que cuando $v$ es mucho menor que $c$ ( $v \ll c$ ), el factor $\gamma \approx 1$, y las ecuaciones se reducen a las conocidas transformaciones de Galileo.

¿Qué proponía Galileo? Galileo formuló las reglas clásicas del movimiento que hoy llamamos “transformaciones galileanas.” Estas resultan válidas únicamente cuando las velocidades implicadas son muy pequeñas en comparación con la velocidad de la luz ($v \ll c$). Según estas transformaciones, si un sistema $S'$ se desplaza con velocidad constante $v$ a lo largo del eje $x$ respecto a un sistema $S$, entonces las coordenadas de un acontecimiento se transforman de la siguiente manera: $$ \begin{cases} x' &= x - vt \\ y' &= y \\ z' &= z \\ t' &= t \end{cases} $$ En esta concepción, el espacio se ve afectado por el movimiento relativo -la coordenada $x'$ refleja el desplazamiento del sistema- mientras que el tiempo es idéntico para todos: $t' = t$ se considera absoluto, independiente del sistema de referencia. En resumen, Galileo sostenía que el tiempo transcurre de manera uniforme para cualquier observador y que las velocidades se suman linealmente. Esta descripción resulta adecuada a bajas velocidades, pero al acercarse a la velocidad de la luz deja de ser válida, y la relatividad especial se convierte en indispensable.

Efectos relativistas

Las transformaciones de Lorentz dan lugar a consecuencias observables y confirmadas experimentalmente. A continuación se resumen las más relevantes.

• Relatividad de la simultaneidad

  Dos sucesos que ocurren en el mismo instante (simultáneos) pero en lugares distintos dentro del sistema inercial $S$, en general no serán simultáneos en el sistema $S'$.

  Solo serán simultáneos en ambos sistemas, $S$ y $S'$, si ocurren exactamente en el mismo punto del espacio. La simultaneidad, por tanto, no es absoluta, sino que depende del marco de referencia. 

  Ejemplo. Dos rayos impactan al mismo tiempo en los extremos de un tren en movimiento para un observador en tierra (sistema $S$). Sin embargo, un pasajero sentado en el centro del tren no los percibe como simultáneos.
  
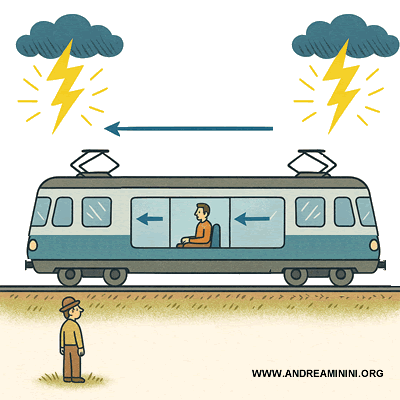
  En el sistema del tren ($S'$), el pasajero está en movimiento: la luz que procede de la parte delantera se acerca hacia él, mientras que la proveniente de la parte trasera debe alcanzarlo. Como consecuencia, los destellos no llegan a la vez. Esta diferencia no es una ilusión óptica, sino la manifestación concreta de que la simultaneidad definida en $S$ (el observador en tierra) no coincide con la simultaneidad en $S'$ (el pasajero).

  Demostración

  Consideremos dos sistemas inerciales, $S$ y $S'$, siendo $S'$ el que se desplaza con velocidad constante $v$ a lo largo del eje $x$ respecto a $S$. La transformación de Lorentz para el tiempo es: $$ t' = \gamma \left( t - \frac{v}{c^2}x \right), $$ donde $$ \gamma = \frac{1}{\sqrt{1 - v^2/c^2}} $$ Supongamos que en $S$ dos sucesos $A$ y $B$ ocurren en posiciones distintas $x_A \neq x_B$ pero en el mismo instante: $$ t_A = t_B. $$ Al ser simultáneos, $$ t_A - t_B = 0 $$ Aplicando la transformación de Lorentz obtenemos: $$ t'_A = \gamma \left( t_A - \frac{v}{c^2}x_A \right), \quad t'_B = \gamma \left( t_B - \frac{v}{c^2}x_B \right) $$ Restando, $$ t'_A - t'_B = \gamma \left( t_A - \frac{v}{c^2}x_A \right) - \gamma \left( t_B - \frac{v}{c^2}x_B \right) $$ $$ t'_A - t'_B = \gamma t_A - \gamma \frac{v}{c^2}x_A - \gamma t_B + \gamma \frac{v}{c^2}x_B $$ Como $t_A = t_B$, los términos en $\gamma t$ se anulan: $$ \require{cancel} t'_A - t'_B = \cancel{\gamma t_A} - \gamma \frac{v}{c^2}x_A - \cancel{\gamma t_B} + \gamma \frac{v}{c^2}x_B $$ $$ t'_A - t'_B = \gamma \frac{v}{c^2}(x_B - x_A) $$ Así, la diferencia temporal $ t'_A - t'_B $ en $S'$ es proporcional a la separación espacial $ x_B - x_A $ en $S$. Los sucesos simultáneos en $S$ pero localizados en puntos distintos dejan de ser simultáneos en $S'$. La simultaneidad se conserva en ambos sistemas únicamente si ocurren en el mismo lugar ($x_A = x_B$).
• Contracción de la longitud
  Un objeto posee una longitud propia $L'$ en el sistema $S'$, donde se encuentra en reposo. Si $S'$ se desplaza con respecto a otro sistema inercial $S$, entonces, desde la perspectiva de un observador en $S$, la longitud del objeto se percibe acortada en la dirección del movimiento: $$ L = \frac{L'}{\gamma} $$ Esta contracción afecta únicamente a la dimensión paralela al desplazamiento, mientras que todas las dimensiones transversales permanecen invariadas.

  Ejemplo. Una varilla de 2 metros en reposo en $S'$ se percibe de solo 1,2 metros para un observador en $S$ cuando $S'$ se desplaza a $0.8c$. $$ \gamma = \frac{1}{\sqrt{1 - 0.8^2}} = \frac{1}{0.6} = 1.666... $$ $$
  L = \frac{2}{1.666...} \approx 1.2 \text{ metros} $$ Lo mismo ocurre con un misil que viaja por el espacio a una velocidad cercana a la de la luz: su longitud se contrae en la dirección del movimiento para un observador, mientras que sus dimensiones transversales permanecen invariadas.
  
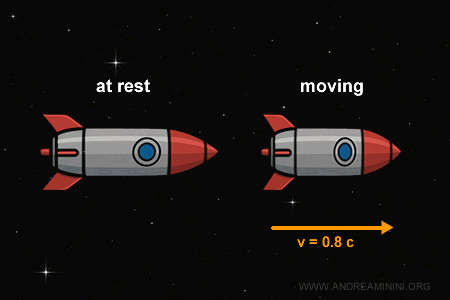
  Por ejemplo, si un misil se mueve hacia la derecha a lo largo del eje $x$, su altura permanece constante ($y = y'$), mientras que su longitud se observa acortada ($x' < x$) debido al fenómeno de contracción de las longitudes.
  

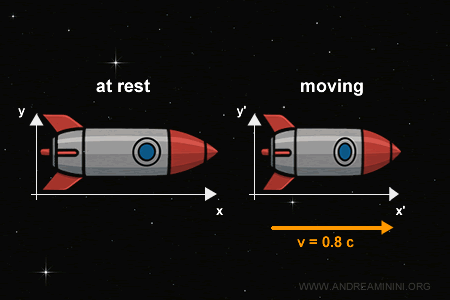
  Demostración de la contracción de la longitud

  Consideremos una varilla rígida de longitud propia $L'$, dispuesta a lo largo del eje $x'$ en su sistema en reposo $S'$.

  Los extremos en este sistema tienen las coordenadas:

  $$ x'_A = 0, \qquad x'_B = L' $$

  En $S'$, la distancia entre los extremos, medida en cualquier instante $t'$, es simplemente

  $$ L' = x'_B - x'_A $$

  Veamos ahora la misma varilla desde otro sistema inercial $S$, donde se desplaza con velocidad $v$ a lo largo del eje $x$.

  Para medir su longitud en $S$, es necesario registrar las posiciones de ambos extremos en el mismo instante $t$, de acuerdo con los relojes de $S$.

  Las transformaciones de Lorentz relacionan las coordenadas en ambos sistemas:

  $$ x' = \gamma (x - vt), \qquad t' = \gamma \left(t - \frac{v}{c^2}x\right) $$

  donde el factor de Lorentz se define como

  $$ \gamma = \frac{1}{\sqrt{1 - v^2/c^2}} $$

  Para el extremo $A$, situado en $x'_A = 0$:

  $$ x'_A = 0 = \gamma (x_A - vt) $$

  $$ \frac{0}{\gamma} = x_A - vt $$

  $$ x_A - vt = 0 $$

  $$ x_A = vt $$

  Para el extremo $B$, situado en $x'_B = L'$:

  $$ x'_B = L' = \gamma (x_B - vt) $$

  $$ \frac{L'}{\gamma} = x_B - vt $$

  $$ x_B = vt + \frac{L'}{\gamma} $$

  Como en el sistema $S$ ambos extremos deben observarse en el mismo instante $t$, la distancia medida resulta

  $$ L = x_B - x_A = \left(vt + \frac{L'}{\gamma}\right) - (vt) = \frac{L'}{\gamma} $$

  Así, en $S$, la longitud de la varilla es menor que su longitud propia $L'$, reducida por un factor $\gamma$.

  $$ L = x_B - x_A = \frac{L'}{\gamma} $$

  En otras palabras, un objeto en movimiento aparece acortado en la dirección de su desplazamiento:

  $$ L = \frac{L'}{\gamma} $$

  Esto deja claro que la contracción de la longitud no implica una compresión física del objeto, sino que es una consecuencia inevitable de la transformación espacio-temporal que vincula a los sistemas inerciales.

  Nota. Ten presente que esta contracción afecta únicamente a la dirección del movimiento. Las dimensiones perpendiculares a la velocidad -como $y$ o $z$, por ejemplo- permanecen inalteradas, ya que las transformaciones de Lorentz no modifican las coordenadas espaciales transversales.

• Dilatación del tiempo
  Un intervalo de tiempo propio $T′$ es la duración medida en el sistema $S′$, donde el reloj permanece en reposo (es decir, en el lugar donde está físicamente instalado). Si el sistema $S′$ se mueve respecto a otro sistema $S$, entonces, desde la perspectiva de un observador en $S$, el tiempo en $S′$ transcurre más despacio: $$ T = \gamma T' $$

  Ejemplo. Un reloj marca $1$ segundo ($T'=1s$) en su propio sistema $ S' $ (una nave espacial) que viaja al 90% de la velocidad de la luz ($v=0.9c$). Para un observador que ve la nave desde un sistema inercial más lento $ S $, el reloj a bordo de $ S' $ parece avanzar con mayor lentitud. $$ \gamma = \frac{1}{\sqrt{1-(0.9)^2}} \approx 2.29 $$ $$ T = \gamma T' \approx 2.29 \ s  $$ Dicho de otro modo, el observador externo percibe que las agujas del reloj de la nave se mueven a cámara lenta.
  

  Derivación de la dilatación temporal
  

  Consideremos un reloj en un sistema $ S' $, por ejemplo, una nave en movimiento o incluso una partícula.

  El intervalo de tiempo $ T' $ entre dos "tic" del reloj (por ejemplo, un segundo) se denomina "tiempo propio". En este caso, los dos sucesos corresponden simplemente a los dos tics del reloj.

  $$ T' = t'_B - t'_A $$

  Para alguien que viaja dentro del sistema $ S' $, el reloj está fijado en la pared. De este modo, ambos tics ocurren en el mismo lugar (el origen), separados por el intervalo de tiempo $T'$.

  • Primer tic: $t'_A=0$ en la posición $ x'_A=0$
  • Segundo tic: $t'_B=T'$ en la posición $ x'_B=0$

  Ahora imaginemos a un observador en un sistema inercial más lento $S$, por ejemplo en la Tierra, que observa cómo $ S' $ (la nave) pasa a gran velocidad $v$. ¿Cómo percibe este observador los tics del reloj de $ S' $? Para responder, aplicamos la transformación de Lorentz para el tiempo:

  $$ t = \gamma \left(t' + \frac{v}{c^2}x'\right), \qquad  \gamma = \frac{1}{\sqrt{1-v^2/c^2}}. $$

  Calculemos los instantes de los dos tics tal como se ven desde el sistema $S$:

  • Primer tic: $t_A = \gamma (0 + \frac{v}{c^2}\cdot 0) = 0$
  • Segundo tic: $t_B = \gamma (T' + \frac{v}{c^2}\cdot 0) = \gamma T'$

  El intervalo de tiempo entre los dos tics en $S$ resulta ser

  $$ T = t_B - t_A = \gamma T' $$

  Como $\gamma \geq 1$, siempre es mayor o igual que uno, lo que implica que $T \geq T'$. En otras palabras: en el sistema $ S $ (la Tierra), donde el reloj se desplaza junto con la nave, el intervalo entre los tics se alarga, $T=\gamma T'$.

  Esto demuestra que el paso del tiempo se dilata en cualquier sistema en movimiento. 

• Adición relativista de velocidades
  En la relatividad especial, las velocidades no se suman de manera lineal como ocurre en la mecánica clásica. Si un objeto se mueve con velocidad \(u'\) respecto a un sistema \(S'\), y este sistema a su vez se desplaza con velocidad \(v\) respecto a otro sistema \(S\), entonces la velocidad del objeto medida en \(S\) no es simplemente \(u = u' + v\). En realidad, se obtiene a partir de la ley relativista: $$ u = \frac{u' + v}{1 + \tfrac{u'v}{c^2}} $$ El denominador garantiza que el resultado nunca pueda superar \(c\), incluso al combinar velocidades muy elevadas. Por ejemplo, si en el sistema \(S'\) un objeto se mueve a la velocidad de la luz (\(u' = c\)), en cualquier otro sistema inercial su velocidad seguirá siendo \(u = c\).   Esta fórmula asegura la invariancia de la velocidad de la luz y deja claro que la regla galileana \(u = u' + v\) solo resulta válida cuando las velocidades son mucho menores que la de la luz \( v \ll c\).
  
  

  Ejemplo. Si una bala viaja a $u' = 0.9c$ en un tren que se desplaza a $v = 0.5c$, su velocidad respecto al suelo no es $1.4c$, sino: $$ u = \frac{0.9c + 0.5c}{1 + \frac{0.9 \cdot 0.5}{1}} = \frac{1.4c}{1 + 0.45} = \frac{1.4c}{1.45} \approx 0.9655c $$

  Demostración

  En mecánica clásica, las velocidades se combinan según la regla galileana: si un objeto se mueve con velocidad \( u' \) respecto a un sistema \( S' \), y este se traslada con velocidad \( v \) respecto a un sistema \( S \), la velocidad del objeto respecto a \( S \) es simplemente

  $$ u = u' + v $$

  Sin embargo, esta regla contradice la relatividad especial, ya que rompería la invariancia de la velocidad de la luz. Por ejemplo, si un objeto en \( S' \) se desplazara a la velocidad de la luz \( c \), la suma clásica daría:

  $$ u = c + v > c $$

  Esto contradice el postulado de Einstein según el cual la velocidad de la luz es siempre la misma constante \( c \) en todos los sistemas inerciales. En cambio, las transformaciones de Lorentz proporcionan la fórmula correcta de adición de velocidades.

  Consideremos una partícula que se mueve a lo largo del eje \( x \) con velocidad \( u' \) en el sistema \( S' \). Su desplazamiento se expresa como:

  $$ u' = \frac{\Delta x'}{\Delta t'} $$

  Desde la perspectiva del sistema \( S \), las transformaciones de Lorentz para los intervalos espaciales y temporales son:

  $$ \Delta x = \gamma (\Delta x' + v \Delta t'), $$ $$ \Delta t = \gamma \left( \Delta t' + \frac{v}{c^2}\Delta x' \right) $$

  Así, la velocidad en el sistema \( S \) resulta ser:

  $$ u = \frac{\Delta x}{\Delta t} = \frac{ \gamma (\Delta x' + v \Delta t')}{ \gamma ( \Delta t' + \tfrac{v}{c^2}\Delta x' )} = \frac{\Delta x' + v \Delta t'}{\Delta t' + \tfrac{v}{c^2}\Delta x'} $$

  Dividiendo numerador y denominador entre $ \Delta t' $ y recordando que $ u'=\Delta x'/\Delta t' $, obtenemos:

  $$ u = \frac{ \frac{ \Delta x' + v \Delta t' }{ \Delta t'  } }{ \frac{ \Delta t' + \tfrac{v}{c^2}\Delta x' }{ \Delta t'  } } = \frac{\dfrac{\Delta x'}{\Delta t'}+v}{1+\dfrac{v}{c^2}\dfrac{\Delta x'}{\Delta t'}} = \frac{u' + v}{1 + \tfrac{u'v}{c^2}} $$

  Esta ley relativista de adición de velocidades mantiene la velocidad de la luz como un límite absoluto, fijando un tope insuperable para cualquier proceso dinámico.

  $$ u = \frac{u' + v}{1 + \tfrac{u'v}{c^2}} $$

  En efecto, si \( u' = c \), entonces \( u = c \) independientemente del valor de \( v \). Del mismo modo, si ambas velocidades son menores que \( c \), su combinación permanece siempre por debajo de \( c \).

  $$ u = \frac{c + v}{1 + \tfrac{cv}{c^2}} = \frac{c + v}{1 + \tfrac{v}{c}}  = \frac{c + v}{1 + \tfrac{v}{c}} \cdot \frac{c}{c}  = \frac{c(c + v)}{c + v} = c$$

  De esto se concluye que la velocidad de la luz es una constante universal que no puede superarse mediante la suma de movimientos relativos.

  Nota. En el límite clásico \( v \ll c \) y \( u' \ll c \), el denominador tiende a la unidad $ 1 + \tfrac{u'v}{c^2} \approx 1 $, y la fórmula relativista se reduce a la regla galileana \( u \simeq u' + v \). $$ u =  \frac{u' + v}{1 + \tfrac{u'v}{c^2}} = \frac{u' + v}{1 + 0 } = u'+v $$ Esto demuestra que la fórmula de Lorentz es plenamente coherente con la mecánica clásica en el régimen no relativista.

Geometría del espacio-tiempo

La relatividad especial no concibe el espacio y el tiempo como realidades separadas e independientes, sino como partes de un mismo entramado geométrico al que llamamos espacio-tiempo.

Cada suceso - es decir, algo que ocurre en un lugar y en un instante precisos - se describe mediante cuatro coordenadas: las tres espaciales \( (x,y,z) \) y la temporal multiplicada por la velocidad de la luz ( ct ). Juntas forman un cuatro-vector $(x, y, z, ct)$.

Las transformaciones de Lorentz conservan una magnitud fundamental llamada intervalo espacio-temporal:

\[  s^2 = c^2 t^2 - x^2 - y^2 - z^2 \]

Este intervalo cumple en el espacio-tiempo el mismo papel que la distancia euclidiana en el espacio ordinario. Así como la distancia permanece invariante frente a las rotaciones tridimensionales, el intervalo espacio-temporal se mantiene invariante bajo las transformaciones de Lorentz.

En definitiva, las transformaciones de Lorentz pusieron fin a la visión clásica de espacio y tiempo al eliminar toda noción de absolutos.

Constituyen el fundamento matemático y conceptual de la relatividad especial y resultan esenciales para comprender fenómenos de altas velocidades, como la física de partículas, la electrodinámica relativista y la cosmología.

Y mucho más.