Diferencia entre tiempo propio y tiempo de laboratorio

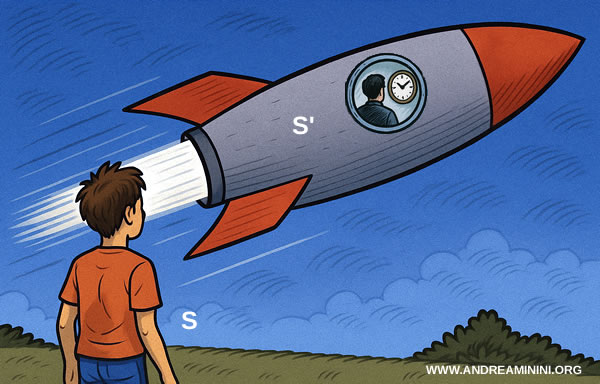
En la relatividad especial, el tiempo propio es el tiempo que mide un reloj que acompaña al objeto en movimiento. El tiempo de laboratorio, en cambio, es el tiempo registrado por un reloj en el sistema inercial del observador.

La distinción surge del principio de relatividad de Einstein: el tiempo no es absoluto; depende del sistema de referencia escogido y de su estado de movimiento.

En otras palabras, cada observador dispone de su propio “tiempo personal”, válido únicamente dentro de su marco de referencia.

Por ejemplo, un reloj instalado en una nave espacial que viaja a velocidades cercanas a la de la luz avanza más despacio que un reloj en reposo en la Tierra.

La relación entre ambas medidas del tiempo se expresa mediante la ecuación:

$$ t = \gamma \tau $$

En esta expresión, la letra griega gamma ($\gamma$) representa el factor de Lorentz, que cuantifica cómo el movimiento relativo afecta a la medida del tiempo entre dos sistemas de referencia:

$$ \gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}} $$

De este modo, la ecuación puede escribirse en su forma completa como:

$$ t = \frac{\tau}{\sqrt{1 - \frac{v^2}{c^2}}} $$

Esta expresión muestra que, a medida que la velocidad $v$ se aproxima a la velocidad de la luz $c$, el tiempo medido en movimiento (t) se dilata respecto al tiempo propio (τ), fenómeno conocido como dilatación temporal.

Donde los símbolos representan:

• $t$: el tiempo de laboratorio, medido por un observador en reposo;
• $\tau$: el tiempo propio, medido en el sistema en movimiento;
• $v$: la velocidad del objeto respecto al observador;
• $c$: la velocidad de la luz en el vacío.

La fórmula indica que cuando $v = 0$, es decir, cuando el objeto está en reposo, se cumple $t = \tau$: ambos relojes marcan el mismo tiempo.

A medida que $v$ aumenta, se verifica que $t > \tau$: el tiempo de laboratorio transcurre más rápido que el tiempo propio.

Y en el límite $v \rightarrow c$, se cumple que $\sqrt{1 - \frac{v^2}{c^2}} \rightarrow 0$, por lo que $t \rightarrow \infty$: el tiempo propio prácticamente se detiene en comparación con el de laboratorio.

Un ejemplo práctico

Supongamos que la nave espacial se desplaza con $v = 0{,}8c$.

Un reloj a bordo registra un intervalo de tiempo propio de:

$$ \tau = 1{,}0 \text{ s} $$

Calculemos el tiempo de laboratorio en la Tierra:

$$ t = \frac{1{,}0}{\sqrt{1 - (0{,}8)^2}} = \frac{1{,}0}{\sqrt{1 - 0{,}64}} = \frac{1{,}0}{\sqrt{0{,}36}} = \frac{1{,}0}{0{,}6} = 1{,}67 \text{ s} $$

Esto significa que por cada segundo que transcurre en el reloj de la nave espacial (punto C), en la Tierra (punto A) pasan 1,67 segundos.

Nota. La dilatación temporal no es solo una predicción teórica: ha sido confirmada experimentalmente, por ejemplo, comparando relojes atómicos transportados en aviones y satélites con otros mantenidos en tierra. Otro caso llamativo es el de la desintegración de los muones: estas partículas inestables, cuando se mueven a velocidades próximas a la de la luz, viven mucho más de lo que indicaría su vida media en reposo.

Y así sucesivamente.