El espín en la mecánica cuántica

El espín es uno de los conceptos más característicos de la física cuántica. Cada partícula elemental lo posee y, junto con otras magnitudes como la energía o el momento angular orbital, ayuda a definir su estado cuántico completo.

Lo primero que conviene aclarar es que el espín no implica que la partícula esté girando físicamente en el espacio. Es un rasgo intrínseco, parte de su identidad, que no puede interpretarse como un movimiento real.

Aun así, matemáticamente se comporta como un tipo especial de momento angular y tiene sus mismas dimensiones físicas. Eso sí, no corresponde a ninguna rotación mecánica de un objeto con extensión.

Ejemplo. El electrón se considera una partícula puntual. No tiene tamaño ni estructura interna, así que no tiene sentido imaginarlo girando como una esfera diminuta.

El espín solo puede tomar valores cuantizados, siempre en múltiplos enteros o semienteros de $\hbar$, la constante de Planck reducida.

$$ s = 0,\ \tfrac{1}{2},\ 1,\ \tfrac{3}{2},\ 2,\ \tfrac{5}{2},\ \dots $$

Según su espín, las partículas se dividen en dos grandes familias:

Bosones, con espín entero. Aquí encontramos a los fotones, los gluones y otras partículas que median interacciones fundamentales.
Fermiones, con espín semientero. Incluyen electrones, protones, neutrones y neutrinos, es decir, los componentes básicos de la materia.

El espín $ \tfrac{1}{2} $ es especialmente importante porque define a las partículas que forman los átomos y, en última instancia, toda la materia cotidiana.

Un electrón con espín $\tfrac{1}{2}$ solo puede encontrarse en dos estados posibles a lo largo de una dirección de observación:

espín arriba: $+\tfrac{1}{2}$
espín abajo: $-\tfrac{1}{2}$

Los espines semienteros no pueden representarse con un vector convencional en tres dimensiones. Se necesita una herramienta matemática diferente: el espinor.

example

Un espinor es un objeto de dos componentes que se transforma según reglas específicas del grupo de rotaciones. Su comportamiento es profundamente cuántico y no tiene equivalente en el mundo macroscópico.

Una de sus propiedades más sorprendentes es esta: si giramos un espinor 360°, no recuperamos el estado inicial, sino el mismo estado con signo opuesto. Solo un giro completo de 720° devuelve exactamente el estado original.

Una buena analogía es la banda de Möbius. Tras un giro de 360°, la orientación queda invertida.

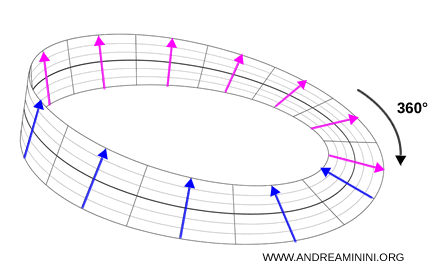
analogía con banda de Möbius que muestra la inversión del espinor tras 360 grados

Si completamos la segunda vuelta, todo vuelve a coincidir.

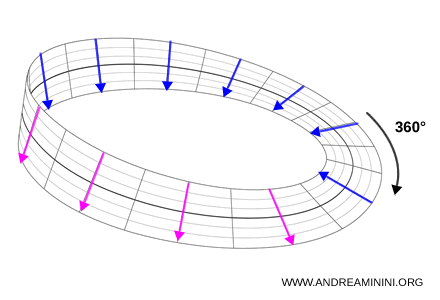
espinor recuperado tras una rotación completa de 720 grados

En el formalismo de Pauli, una partícula con espín 1/2 se representa mediante un espinor de dos componentes:

$$ \chi = \begin{pmatrix} \alpha \\ \beta \end{pmatrix} $$

Los números complejos $\alpha$ y $\beta$ contienen la información probabilística sobre medir el espín arriba o abajo.

Nota. Cuando rotamos el sistema de coordenadas, el espinor se transforma con un operador unitario: $$ \begin{pmatrix} \alpha' \\ \beta' \end{pmatrix} = U(\theta) \begin{pmatrix} \alpha \\ \beta \end{pmatrix} $$ donde $ U(\theta) $ tiene la forma $$ U(\theta) = e^{- i \theta \cdot \sigma /2} $$ y $ \theta $ define el eje y el ángulo de giro.

Cómo se representan las partículas según su espín

La forma en que representamos matemáticamente una partícula depende directamente de su espín. Las diferencias son profundas.

Espín 1. Los bosones vectoriales, como el fotón, se representan con vectores de tres componentes. Sus rotaciones siguen las reglas del grupo $ SO(3) $.
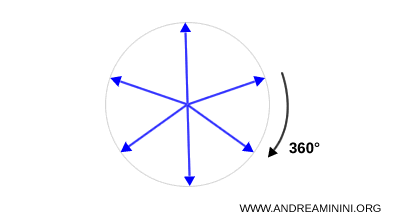
Espín $ \tfrac{1}{2} $. Aquí entran los espinores. Sus transformaciones pertenecen al grupo $ SU(2) $, que es la doble cubierta de $ SO(3) $. Por eso necesitan un giro de 720° para volver exactamente a su estado inicial.

Nota. Las representaciones $ 3 \times 3 $ de $ SO(3) $ y las representaciones $ 2 \times 2 $ de $ SU(2) $ ilustran la diferencia fundamental entre espines enteros y semienteros.
Espín $ \tfrac{3}{2} $. Se necesitan espinores de cuatro componentes, que siguen la representación de cuatro dimensiones de $ SU(2) $. Presentan las mismas propiedades cuánticas típicas de todos los espines semienteros.

Resumiendo:

Espín 0: representación escalar (1 dimensión)
Espín $ \tfrac{1}{2} $: representación espinorial (2 dimensiones)
Espín 1: representación vectorial (3 dimensiones)
Espín $ \tfrac{3}{2} $: representación espinorial de mayor dimensión (4 dimensiones)

El espín en la teoría cuántica de campos

En la mecánica cuántica no relativista, el espín se introdujo para explicar fenómenos como la estructura fina de los espectros atómicos o el efecto Zeeman. Pero su comprensión completa requiere el marco relativista.

En la mecánica cuántica relativista, el espín surge de forma natural a partir de la ecuación de Dirac, que describe cómo se comporta el electrón. Esta ecuación predice de manera automática el espín $\tfrac{1}{2}$ y explica resultados experimentales fundamentales, como el momento magnético anómalo.

El formalismo de Dirac sostiene ideas clave como:

El principio de exclusión de Pauli, que impide que dos fermiones idénticos estén en el mismo estado cuántico.
La estadística cuántica, que distingue entre bosones (Bose Einstein) y fermiones (Fermi Dirac).
El origen de los momentos magnéticos de las partículas fundamentales, en los que el espín desempeña un papel decisivo.

El espín es un ejemplo claro de una propiedad puramente cuántica, sin ningún equivalente en la física clásica.

Aunque nació para resolver anomalías experimentales, solo adquiere su significado pleno en el marco relativista. Gracias a los espinores entendemos su estructura, su comportamiento y su papel en la física de partículas y en la materia misma.

Y la exploración continúa.