Decaimiento de partículas

El decaimiento de partículas es el proceso espontáneo por el cual una partícula inestable se transforma en otras más ligeras y estables.

En términos generales, las partículas tienden de manera natural a evolucionar hacia estados más estables, salvo que alguna ley de conservación lo impida.

Esta transformación puede producirse a través de diferentes canales de decaimiento (interacciones fuerte, débil o electromagnética), cada uno caracterizado por su probabilidad y su tiempo de vida típico.

El proceso está gobernado por dos principios esenciales:

• Tendencia hacia estados de menor energía
  Una partícula inestable se desintegra en una configuración con menor masa total. Es un proceso natural de relajación, semejante a la caída de un objeto bajo la gravedad.
  

  Nota. En mecánica clásica, un objeto inestable acaba cayendo al suelo hasta alcanzar el equilibrio. En química, un átomo inestable se reorganiza hasta lograr un estado más estable. En física de partículas, el decaimiento cumple una función análoga: la partícula se transforma de manera espontánea en productos más estables, con una cierta probabilidad y un tiempo de vida medio característico.

• Leyes de conservación
  No todo decaimiento energéticamente posible está permitido. La transformación debe respetar las leyes de conservación fundamentales: energía y momento, carga eléctrica, número bariónico y leptónico, sabor de los quarks (conservado en las interacciones fuerte y electromagnética, pero no siempre en la débil), espín, paridad y otros.

El decaimiento no es, por tanto, un proceso aleatorio: obedece a probabilidades de transición bien definidas y se cuantifica a través del tiempo de vida medio de la partícula.

Conviene subrayar que las partículas realmente estables son muy escasas: la inmensa mayoría acaba desintegrándose.

En física de partículas, el decaimiento es la regla; la estabilidad, la excepción.

Ejemplo. Un caso clásico es el decaimiento de un neutrón libre. Fuera del núcleo atómico, el neutrón es inestable y se desintegra por interacción débil en un protón, un electrón y un antineutrino electrónico. Este proceso se conoce como decaimiento beta menos: $$ n \to p + e^- + \bar{\nu}_e $$ De esta forma, el neutrón pasa a un estado de menor energía y más estable: el protón.

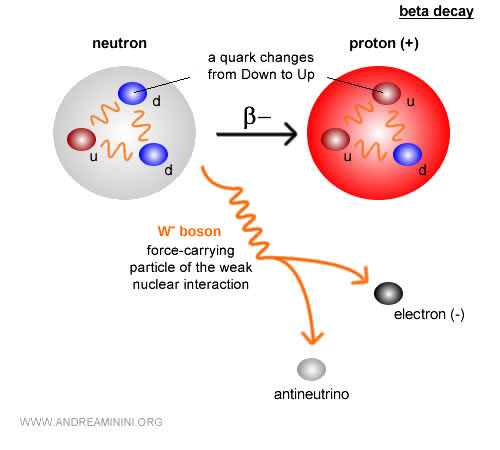
¿Por qué el protón es estable? El protón permanece estable porque es el barión más ligero: no existe ningún barión más liviano en el que pueda transformarse sin violar la conservación del número bariónico. Un decaimiento en partículas no bariónicas rompería esa conservación, que se cumple en todas las interacciones conocidas. Por ello, dentro del Modelo Estándar se considera estable. Ahora bien, algunas teorías especulativas predicen un eventual decaimiento del protón en escalas de tiempo inconcebiblemente largas, aunque nunca se ha observado.

Canales de decaimiento

Una partícula puede desintegrarse por distintos canales, según la interacción fundamental que gobierne el proceso.

• Interacción fuerte
  Responsable de la desintegración de resonancias hadrónicas, que se transforman casi de manera instantánea. Es el canal más rápido, con tiempos de vida típicos de unos $10^{-23}$ s. Por ejemplo, el barión $\Delta^{++}$ se desintegra en un protón y un pión positivo: $$ \Delta^{++} \to p^+ + \pi^- $$
• Interacción débil
  Permite procesos que modifican el sabor de los quarks o que involucran leptones. Es el canal más lento, con tiempos de vida que van desde $10^{-13}$ s hasta varios minutos. Un caso bien conocido es el del muón negativo $\mu^-$, que se desintegra en un electrón, un antineutrino electrónico y un neutrino muónico: $$ \mu^- \to e^- + \bar{\nu}_e + \nu_{\mu} $$
• Interacción electromagnética
  Implica la emisión de fotones y se da cuando la carga eléctrica o los momentos magnéticos desempeñan un papel fundamental. Es más lenta que las desintegraciones fuertes, con tiempos de vida del orden de $10^{-16}$ s. Un ejemplo es el pión neutro $\pi^0$, que se desintegra en dos fotones: $$ \pi^0 \to \gamma + \gamma $$

Identificación del canal de decaimiento

El canal puede deducirse a menudo observando los productos finales:

La presencia de fotones señala un proceso electromagnético. Los neutrinos delatan un decaimiento débil. Si no aparecen ni fotones ni neutrinos, lo más probable es que se trate de un proceso fuerte.

En algunos casos, sin embargo, distintas interacciones pueden conducir a los mismos estados iniciales y finales, lo que complica identificar cuál es la responsable.

Un criterio eficaz consiste en estudiar los tiempos de vida, ya que cada interacción se manifiesta en una escala temporal característica:

• interacción fuerte ≈ $10^{-23}$ s
• interacción electromagnética ≈ $10^{-16}$ s
• interacción débil $\gtrsim 10^{-13}$ s

Las desintegraciones fuertes son extremadamente fugaces. Las electromagnéticas son más lentas en varios órdenes de magnitud, mientras que las débiles son las más prolongadas, con tiempos de vida que abarcan desde fracciones de microsegundo hasta varios minutos, como en el caso del neutrón.

Otro criterio es estadístico: cada canal de decaimiento posee una probabilidad de ocurrencia, expresada mediante los “branching ratios”.

Branching Ratios

Los “branching ratios” describen la probabilidad relativa de que una partícula inestable se desintegre por un canal u otro.

En otras palabras, una partícula puede presentar varios modos de decaimiento posibles, cada uno con su probabilidad, y la suma total debe ser del 100%.

Formalmente, el branching ratio de un canal se define como

$$ BR_i = \frac{\Gamma_i}{\Gamma_{\text{tot}}} $$

donde $\Gamma_i$ es la anchura parcial de decaimiento de ese canal y $\Gamma_{\text{tot}}$ es la anchura total (el inverso del tiempo de vida medio).

Por ejemplo, la partícula $\Delta^0$ se desintegra en un protón y un pión negativo: $$ \Delta^0 \;\to\; p + \pi^- $$ En principio, este decaimiento podría producirse tanto por interacción fuerte como por interacción débil. En la práctica, la $\Delta^0$ se desintegra casi exclusivamente mediante la interacción fuerte, con un tiempo de vida del orden de $10^{-23}$ s. El canal débil, mediado por un bosón $W^-$, es teóricamente posible pero tan suprimido que resulta inobservable: el canal fuerte lo domina por completo.

Tiempo de vida medio de una partícula

El tiempo de vida medio de una partícula depende no solo de la interacción que provoca el decaimiento (fuerte, electromagnética o débil), sino también de la diferencia de masa entre el estado inicial y los productos finales.

• Si la diferencia de masa es grande, el decaimiento es rápido, ya que hay más energía disponible y más estados finales accesibles.
• Si la diferencia de masa es pequeña, el proceso se ralentiza: la partícula solo puede desintegrarse de manera más gradual.

El tiempo de vida medio viene determinado, por tanto, tanto por la interacción implicada como por la diferencia de masa.

Esta regla se cumple en general, con contadas excepciones.

Ejemplo. Un neutrón libre tiene una masa apenas superior a la de un protón más un electrón. Como consecuencia, el decaimiento beta menos presenta un tiempo de vida medio inusualmente largo - unos 15 minutos - en comparación con la escala típica de la interacción débil, del orden de $\sim 10^{-13}$ s: $$ n \;\to\; p + e^- + \bar{\nu}_e $$ Por el contrario, las resonancias $\Delta$ poseen una gran diferencia de masa con respecto a sus productos de desintegración (un nucleón más un pión) y, por ello, se desintegran casi de inmediato mediante la interacción fuerte, con tiempos característicos del orden de $10^{-23}$ s: $$ \Delta^0 \;\to\; p + \pi^- $$

Y así sucesivamente.