Antipartículas
Cada partícula elemental posee una antipartícula asociada, con la misma masa y espín, pero con cargas aditivas opuestas (eléctrica, bariónica, leptónica, etc.).
Una antipartícula no es simplemente una imagen en espejo: se trata de una entidad distinta, con un papel físico bien definido en las interacciones.
Algunos ejemplos son:
| Partícula | Antipartícula |
|---|---|
| Electrón $e^-$ | Positrón $e^+$ |
| Protón $p $ | Antiprotón $\overline{p} $ |
| Neutrón $n $ | Antineutrón $\overline{n} $ |
| Quark $u $ | Antiquark $\overline{u} $ |
Por ejemplo, la antipartícula del electrón (carga eléctrica negativa) es el positrón, que tiene la misma masa y espín pero con carga positiva.
La del protón (carga positiva) es el antiprotón, que porta una carga negativa, y así sucesivamente.
Nota. Por convención, las antipartículas suelen representarse con una barra sobre el símbolo de la partícula. Así, la antipartícula del protón $p$ se denota $ \overline{p} $. Sin embargo, existen excepciones: el positrón (antielectrón) casi siempre se escribe como $ e^+ $ en lugar de $ \overline{e} $, y el antimuón como $ \mu^+ $ en lugar de $ \overline{\mu} $.
Conviene subrayar que la “oposición” de cargas no tiene por qué ser eléctrica. Una antipartícula puede diferenciarse en otros números cuánticos aditivos, como el número bariónico, el número leptónico u otros números cuánticos.
Por ejemplo, el neutrón no posee carga eléctrica, por lo que su antipartícula -el antineutrón- no se distingue por la carga, sino por otros números cuánticos.
Algunas partículas coinciden con sus propias antipartículas. Estas se denominan partículas autoconjugadas.
Una partícula es autoconjugada cuando resulta indistinguible de su antipartícula; es decir, cuando su carga eléctrica y todas las demás cargas aditivas son nulas.
Ejemplos de partículas autoconjugadas son:
| Partícula | ¿Autoconjugada? | Observaciones |
|---|---|---|
| Fotón $ \gamma $ | Sí | Carece de carga |
| Bosón $Z^0 $ | Sí | Neutro |
| Mesón $\pi^0 $ | Sí | Pión neutro |
| Gluones | Sí / No | Depende de la configuración |
En el caso de los neutrinos, todavía se desconoce si son neutrinos de Dirac (con antipartículas diferenciadas) o neutrinos de Majorana (autoconjugados). Esta cuestión sigue abierta en la física de partículas.
Diferencia entre antipartículas y antimateria
La materia compuesta exclusivamente por antipartículas recibe el nombre de antimateria.
La antimateria presenta una característica notable: cuando materia y antimateria se encuentran, se aniquilan liberando energía en forma de fotones gamma.
$$ e^- + e^+ \rightarrow \gamma + \gamma $$
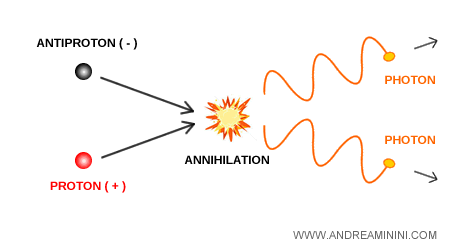
Ahora bien, la mera existencia de un positrón aislado no basta para hablar de antimateria. Para ello es necesario un sistema estructurado, como un antiátomo o una molécula estable de antimateria.
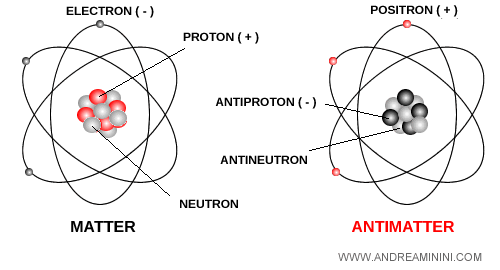
En otras palabras, la antimateria se construye a partir de antipartículas, pero no toda antipartícula por sí sola constituye antimateria.
Ejemplo. Un átomo de antihidrógeno está formado por un antiprotón $ \overline{p} $ en el núcleo y un positrón $ e^+ $ (la contraparte de antimateria del electrón) orbitando a su alrededor. A diferencia del hidrógeno, las cargas del protón y del electrón están invertidas. Como estas antipartículas forman una estructura estable y eléctricamente neutra, el antihidrógeno sí se considera antimateria. En cambio, un positrón aislado o un antineutrino que recorre el espacio sigue siendo únicamente una antipartícula, no antimateria.
Por tanto, aunque estén estrechamente vinculadas, antimateria y antipartículas no son lo mismo.
La antimateria es una forma estructurada de materia compuesta por antipartículas ligadas, mientras que las antipartículas también pueden existir de manera independiente sin dar lugar a antimateria.
El descubrimiento de las antipartículas
En 1927, el físico Paul Dirac se propuso formular una ecuación capaz de describir el comportamiento de los electrones libres de manera consistente tanto con la mecánica cuántica como con la relatividad.
Lo consiguió al llegar a la siguiente expresión:
$$ E^2 - p^2c^2 = m^2c^4 $$
Sin embargo, la ecuación tenía un rasgo desconcertante: admitía dos tipos de soluciones energéticas:
$$ E = \pm \sqrt{p^2 c^2 + m^2 c^4} $$
La solución positiva, $ E = + \sqrt{p^2 c^2 + m^2 c^4} $, resultaba natural: describía un electrón con energía positiva, tal y como se espera en cualquier partícula ordinaria.
La solución negativa, $ E = - \sqrt{p^2 c^2 + m^2 c^4} $, planteaba un problema más serio: parecía sugerir la existencia de electrones en estados de energía negativa.
¿Qué ocurriría si un electrón pudiera realmente ocupar esos estados de energía negativa?
Según la mecánica cuántica, los sistemas tienden de forma natural a minimizar su energía.
De ser así, un electrón en un estado de energía positiva descendería espontáneamente a estados de menor energía siempre que tuviera la posibilidad.
Pero la ecuación de Dirac permitía una escala infinita de niveles de energía negativa. Si estos fueran accesibles, un electrón caería indefinidamente, emitiendo un fotón en cada transición.
El resultado sería una inestabilidad catastrófica: la materia radiaría energía sin límite, hasta desaparecer por completo.
Para resolver esta paradoja, Dirac propuso una idea revolucionaria: todos los estados de energía negativa ya están ocupados por electrones invisibles, formando lo que denominó el “mar de Dirac”.
Este mar de electrones impregnaría el universo pero permanecería invisible: perfectamente uniforme, inerte e inobservable, sin ejercer fuerzas ni generar interacciones con la materia ordinaria.
Ahora bien, si uno de estos estados quedaba vacío -dejando un “hueco” en el mar-, ese hueco se comportaría como una partícula con energía positiva, carga positiva y la misma masa que el electrón.
Esa partícula es lo que hoy conocemos como el positrón, la antipartícula del electrón.
Nota. En un primer momento, Dirac conjeturó que esos “huecos” podrían corresponder a protones. Pronto descartó la hipótesis, ya que la masa del protón es miles de veces mayor que la del electrón.
En 1932, Carl Anderson observó experimentalmente el primer positrón, confirmando de manera contundente la predicción de Dirac.
Sin embargo, la noción del “mar de electrones” fue abandonada en la década de 1940, cuando Stueckelberg y Feynman reinterpretaron los positrones como auténticas partículas de energía positiva.
Desde entonces, los positrones se consideran partículas reales, y no simples “huecos” en un medio imaginario.
Este avance condujo rápidamente a la idea general de que toda partícula debe poseer una antipartícula correspondiente, con la misma masa pero carga opuesta.
En los años cincuenta, los experimentos en el Bevatron de Berkeley confirmaron esta visión con el descubrimiento del antiprotón y el antineutrón.
Simetría de cruce
La simetría de cruce es un principio según el cual se pueden generar nuevos procesos, teóricamente equivalentes a uno ya conocido, sustituyendo una partícula por su antipartícula y trasladándola al lado opuesto de la ecuación de reacción.
Se trata de una simetría fundamental en la física de partículas:
Ejemplo
La dispersión Compton y la aniquilación electrón-positrón están relacionadas por esta simetría.
La dispersión Compton es un proceso bien conocido y fácilmente reproducible en laboratorio:
$$\gamma + e^- \rightarrow \gamma + e^-$$
Un fotón ($\gamma$) incide sobre un electrón libre, se dispersa (cambiando su dirección y su longitud de onda) y el electrón resulta desviado.
Este es el ejemplo paradigmático de dispersión: partícula + partícula $\;\to\;$ partícula + partícula.
La simetría de cruce afirma que, si un proceso es posible, entonces (al menos teóricamente) también deben serlo otros, obtenidos trasladando partículas de un lado al otro de la ecuación y sustituyéndolas por sus antipartículas.
Consideremos de nuevo la dispersión Compton:
$$ \gamma + e^- \rightarrow \gamma + e^- $$
Aplicando la simetría de cruce, se puede transformar en otro proceso equivalente.
Primero, trasladamos el fotón inicial al lado derecho, reemplazándolo por su antipartícula -que en este caso sigue siendo un fotón, pues es una partícula autoconjugada-:
$$ e^- \rightarrow \gamma + \gamma + e^- $$
A continuación, movemos el electrón final $ e^- $ al lado izquierdo y lo sustituimos por su antipartícula, el positrón $ e^+ $:
$$ e^- + e^+ \rightarrow \gamma + \gamma $$
Este es el proceso de aniquilación electrón-positrón, igualmente real y confirmado experimentalmente.
En otras palabras, la simetría de cruce muestra que, desde el punto de vista matemático, ambas reacciones son manifestaciones distintas de la misma dinámica cuántica subyacente.
Esto pone de relieve una profunda unidad en la física: procesos aparentemente distintos obedecen a los mismos principios fundamentales.
Nota. Aunque las dos reacciones están vinculadas matemáticamente, no son físicamente idénticas. La dispersión Compton ($\gamma + e^- \rightarrow \gamma + e^-$) se produce cuando los fotones se dispersan en electrones libres de un gas o de un metal, mientras que la aniquilación ($e^- + e^+ \rightarrow \gamma + \gamma$) ocurre cuando electrones y positrones se encuentran y se destruyen mutuamente. La simetría se aplica a la estructura teórica, no a las condiciones experimentales.
Y así sucesivamente.