Diagramas de Young en la simetría SU(3)

Los diagramas de Young son una herramienta gráfica esencial para representar, de forma clara y ordenada, las representaciones del grupo SU(3) y para entender cómo dichas representaciones se combinan mediante productos tensoriales.

En física de partículas, la simetría SU(3) describe la simetría de sabor asociada a los quarks up, down y strange ( u,d,s ).

Gracias a su carácter visual, los diagramas de Young se utilizan de manera habitual para clasificar mesones, bariones y multipletes de partículas según sus propiedades de simetría.

Qué es un diagrama de Young

Un diagrama de Young es una herramienta fundamental para describir simetrías en teoría de grupos y física de partículas. Está formado por casillas organizadas en filas alineadas a la izquierda, de tal modo que la longitud de las filas no aumenta al descender desde la fila superior hacia las inferiores.

En el caso de SU(3), la representación fundamental se describe mediante un diagrama con una única casilla. Su dimensión es $ 3 $ y, desde el punto de vista físico, corresponde al triplete de quarks \(  \{ u,d,s \} \).

Algunos ejemplos habituales de diagramas de Young son una sola casilla (1), dos casillas en una fila (2), dos casillas en una columna (1,1), dos casillas en la fila superior con una situada inmediatamente debajo (2,1), así como otras configuraciones similares que respetan las reglas de construcción.

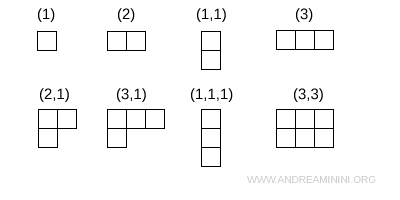
Cada diagrama de Young caracteriza un tipo de simetría bien definido para los índices de una representación tensorial y permite identificar de forma sistemática las representaciones irreducibles asociadas.

Reglas básicas para SU(3)

Al trabajar con diagramas de Young en el grupo SU(3), se deben tener en cuenta las siguientes reglas fundamentales.

1. Cada casilla representa un índice tensorial que transforma según la representación fundamental \( 3 = \{ u,d,s \} \).
2. Las casillas dispuestas en una misma fila indican la simetrización de los índices correspondientes.
3. Las casillas dispuestas en una misma columna indican la antisimetrización de los índices correspondientes.
4. El diagrama debe estar formado por filas cuya longitud no aumente al pasar de arriba hacia abajo.
5. En SU(3), ningún diagrama de Young puede tener más de tres filas, ya que la antisimetrización completa de cuatro índices se anula de manera idéntica. Esta restricción es esencial, pues limita de forma automática el conjunto de representaciones admisibles.
6. Producto tensorial
   En un producto tensorial, por ejemplo $ 6 \otimes 3 $, las casillas asociadas al segundo factor se añaden una a una al diagrama de Young del primer factor. Este procedimiento permite generar todos los diagramas que respetan las reglas de Young. Cualquier configuración que infrinja alguna de estas reglas debe descartarse. Si en algún paso una casilla no admite ninguna posición permitida, se dice que el canal correspondiente se cierra.
   • Antisimetría en columna
     En el producto tensorial, las casillas que pertenecen a una columna antisimétrica
     1] no pueden colocarse todas en una misma fila
     2] solo pueden colocarse todas en una misma columna si prolongan una columna ya existente en el diagrama original 
   • Comprobación final de la dimensión
     La suma de las dimensiones de todos los diagramas admisibles debe coincidir con la dimensión total del producto tensorial. Por ejemplo, en $ 6 \otimes 3 $ hay $ 6 \times 3 = 18 $ estados, de modo que la suma de las representaciones resultantes también debe ser 18, como en el caso $ 15 \oplus 3 $.  Si algunos canales se cierran y parte de la dimensión total no queda representada, la contribución restante se obtiene por sustracción y se identifica con la representación compatible.

¿Por qué son tan útiles los diagramas de Young? Los diagramas de Young permiten visualizar de inmediato las propiedades de simetría de una representación. Gracias a ello, es posible identificar qué representaciones son admisibles y qué combinaciones de quarks están permitidas sin recurrir a cálculos algebraicos largos y poco intuitivos. De este modo, el álgebra abstracta de SU(3) se traduce en un lenguaje geométrico discreto y fácil de interpretar. Los diagramas de Young no dicen qué partículas existen, sino qué estructuras de simetría son posibles. El grupo SU(3) fija el marco teórico y los diagramas de Young ofrecen una lectura directa de ese marco.

Posibles combinaciones de multipletes

Para calcular la dimensión de los multipletes asociados a un diagrama de Young en la simetría SU(3), se utiliza la siguiente fórmula:

\[ \dim = \prod_{\text{boxes}} \ \frac{N + c - r}{h} \]

donde

• \( N \) es la dimensión de la representación fundamental del grupo. Por ejemplo, para SU(2) se tiene N = 2, para SU(3) N = 3, para SU(4) N = 4, y así sucesivamente.
• \( r \) es el índice de fila de una casilla en el diagrama de Young, contado de arriba hacia abajo comenzando en 0.
• \( c \) es el índice de columna de una casilla en el diagrama de Young, contado de izquierda a derecha comenzando en 0.
• \( h \) es la longitud del gancho de la casilla, definida como \[ h = (\text{número de casillas a la derecha}) + (\text{número de casillas debajo}) + 1 \], donde el término \( +1 \) corresponde a la propia casilla.

El producto se toma sobre todas las casillas que forman el diagrama de Young.

Nota. El factor $ (c - r) $ depende únicamente de la posición de la casilla dentro del diagrama, mientras que la longitud del gancho \( h \) depende solo de la forma del diagrama. Esta fórmula es válida para cualquier diagrama de Young en SU(N) y no requiere correcciones adicionales.

Un ejemplo práctico

Combinación de dos quarks: \( 3 \otimes 3 \)

Consideremos el producto tensorial de dos representaciones fundamentales \( 3 = \{ u,d,s \} \).

$$ 3 \otimes 3 $$

La representación $ 3 $ se representa mediante una única casilla que porta los índices \(  \{ u,d,s \} \).

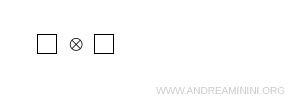
Para evaluar este producto tensorial con diagramas de Young, se añade una segunda casilla a la primera en todas las posiciones permitidas por las reglas anteriores. De este procedimiento surgen dos configuraciones diferentes:

1. Dos casillas en una fila
   Las casillas se sitúan en la misma fila, lo que indica una combinación simétrica. Esta configuración corresponde a la representación \( 6 \).
   
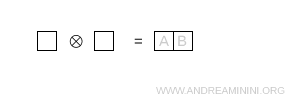   Nota. Para calcular la dimensión se evalúa el producto de las contribuciones de cada casilla usando \[ \dim = \prod_{\text{boxes}} \ \frac{N + c - r}{h} \]. En este caso N = 3, ya que el grupo es SU(3).
   

   • Casilla A. El índice de fila es $ r=0 $, el índice de columna es $ c=0 $. Hay una casilla a la derecha y ninguna debajo, por lo que $ h=1+0+1=2 $.  $$ \frac{N + c - r}{h}  = \frac{3 + 0 - 0}{2} = \frac{3}{2} $$
   • Casilla B. El índice de fila es $ r=0 $, el índice de columna es $ c=1 $. No hay casillas a la derecha ni debajo, de modo que $ h=0+0+1=1 $.  $$ \frac{N + c - r}{h}  = \frac{3 + 1 - 0}{1} = 4 $$

   El producto de estos factores da la dimensión $$ dim = \frac{3}{2} \cdot 4 = 6 $$ Al tratarse de un diagrama horizontal, la representación es simétrica y corresponde a $ 6 $.
2. Dos casillas en una columna
   Las casillas se disponen verticalmente, lo que indica una combinación antisimétrica. Esta configuración corresponde a la representación \( \bar{3} \).
   
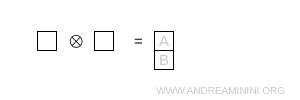   Nota. La dimensión se obtiene de nuevo a partir de \[ \dim = \prod_{\text{boxes}} \ \frac{N + c - r}{h} \], con N = 3 para SU(3).
   

   • Casilla A. El índice de fila es $ r=0 $, el índice de columna es $ c=0 $. No hay casillas a la derecha y hay una casilla debajo, por lo que $ h=0+1+1=2 $.  $$ \frac{N + c - r}{h}  = \frac{3 + 0 - 0}{2} = \frac{3}{2} $$
   • Casilla B. El índice de fila es $ r=1 $, el índice de columna es $ c=0 $. No hay casillas a la derecha ni debajo, por lo tanto $ h=0+0+1=1 $.  $$ \frac{N + c - r}{h}  = \frac{3 + 0 - 1}{1} = 2 $$

   El producto conduce a la dimensión $$ dim = \frac{3}{2} \cdot 2 = 3 $$ La disposición vertical codifica la antisimetría, por lo que esta representación es \( \bar 3 \).

El resultado final es, por tanto,

\[ 3 \otimes 3 = 6 \oplus \bar{3} \]

Desde un punto de vista físico, esta descomposición indica que el producto tensorial de dos tripletes de quarks se divide en seis pares de quarks simétricos y tres pares de quarks antisimétricos.

Nota. Este resultado encaja perfectamente con la intuición física. Un par de quarks es simétrico si el intercambio de los dos quarks no modifica el estado, y es antisimétrico si dicho intercambio introduce un signo menos global. Para los tres sabores de quarks ( \( u,d,s \) ) existen seis pares simétricos. \[ uu \xrightarrow{\text{intercambio}} uu  \] \[ dd \xrightarrow{\text{intercambio}} dd \] \[ ss \xrightarrow{\text{intercambio}} ss \] \[ ud+du \xrightarrow{\text{intercambio}} du+ud = ud+du \] \[ us+su \xrightarrow{\text{intercambio}} su+us = us+su \] \[ ds+sd \xrightarrow{\text{intercambio}} sd+ds =  ds+sd \] Asimismo, existen tres pares antisimétricos. \[ ud-du \xrightarrow{\text{intercambio}} du-ud = - (ud - du) \] \[ us-su \xrightarrow{\text{intercambio}} su-us = - (us - su) \] \[ ds-sd \xrightarrow{\text{intercambio}} sd-ds = - (ds - sd) \]

Combinación de tres quarks: \( 3 \otimes 3 \otimes 3 \)

Este es el caso clave para comprender la estructura de los bariones dentro de la simetría SU(3).

$$ 3 \otimes 3 \otimes 3 $$

A partir del resultado obtenido para $ 3 \otimes 3 $ (con dos casillas dispuestas en horizontal o en vertical), se incorpora una tercera casilla. Al aplicar las reglas de los diagramas de Young, se obtienen las siguientes configuraciones permitidas:

1. Tres casillas en una fila
   Esta es la configuración completamente simétrica y da lugar a la representación decuplete \( 10 \).
   
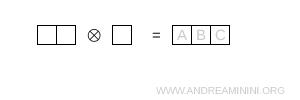   Nota. La dimensión se obtiene multiplicando las contribuciones de cada casilla mediante la fórmula \[ \dim = \prod_{\text{boxes}} \ \frac{N + c - r}{h} \], con N = 3.
   

   • Casilla A. Índice de fila $ r=0 $, índice de columna $ c=0 $. Hay dos casillas a la derecha y ninguna debajo, por lo que $ h=2+0+1=3 $.  $$ \frac{N + c - r}{h}  = \frac{3 + 0 - 0}{3} = 1 $$
   • Casilla B. Índice de fila $ r=0 $, índice de columna $ c=1 $. Hay una casilla a la derecha y ninguna debajo, de modo que $ h=1+0+1=2 $.  $$ \frac{N + c - r}{h}  = \frac{3 + 1 - 0}{2} = 2 $$
   • Casilla C. Índice de fila $ r=0 $, índice de columna $ c=2 $. No hay casillas a la derecha ni debajo, por lo que $ h=0+0+1=1 $.  $$ \frac{N + c - r}{h}  = \frac{3 + 2 - 0}{1} = 5 $$

   El producto de estos factores conduce a la dimensión $$ dim = 1 \cdot 2 \cdot 5 = 10 $$ Al tratarse de un diagrama horizontal, la representación es totalmente simétrica y corresponde al decuplete $ 10 $.
2. Dos casillas en la primera fila y una en la segunda fila
   Esta configuración presenta una simetría mixta y corresponde a la representación octete \( 8 \).
   
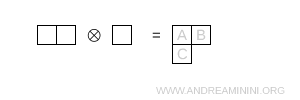   Nota. La dimensión se calcula nuevamente usando \[ \dim = \prod_{\text{boxes}} \ \frac{N + c - r}{h} \], con N = 3.
   

   • Casilla A. Índice de fila $ r=0 $, índice de columna $ c=0 $. Hay una casilla a la derecha y una debajo, por lo que $ h=1+1+1=3 $.  $$ \frac{N + c - r}{h}  = \frac{3 + 0 - 0}{3} = 1 $$
   • Casilla B. Índice de fila $ r=0 $, índice de columna $ c=1 $. No hay casillas a la derecha ni debajo, de modo que $ h=0+0+1=1 $.  $$ \frac{N + c - r}{h}  = \frac{3 + 1 - 0}{1} = 4 $$
   • Casilla C. Índice de fila $ r=1 $, índice de columna $ c=0 $. No hay casillas a la derecha ni debajo, por lo que $ h=0+0+1=1 $.  $$ \frac{N + c - r}{h}  = \frac{3 + 0 - 1}{1} = 2 $$

   El producto da como resultado la dimensión $$ dim = 1 \cdot 4 \cdot 2 = 8 $$ Este diagrama de Young corresponde, por tanto, al octete $ 8 $.
3. Tres casillas en una columna
   Esta es la configuración completamente antisimétrica y conduce a la representación singlete \( 1 \).
   
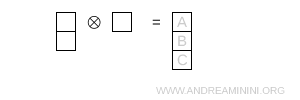   Nota. Aplicando de nuevo la fórmula con N = 3:
   \[ \dim = \prod_{\text{boxes}} \ \frac{N + c - r}{h} \].
   

   • Casilla A. Índice de fila $ r=0 $, índice de columna $ c=0 $. Hay dos casillas debajo y ninguna a la derecha, por lo que $ h=0+2+1=3 $.  $$ \frac{N + c - r}{h}  = 1 $$
   • Casilla B. Índice de fila $ r=1 $, índice de columna $ c=0 $. Hay una casilla debajo y ninguna a la derecha, de modo que $ h=0+1+1=2 $.  $$ \frac{N + c - r}{h}  = 1 $$
   • Casilla C. Índice de fila $ r=2 $, índice de columna $ c=0 $. No hay casillas a la derecha ni debajo, por lo que $ h=0+0+1=1 $.  $$ \frac{N + c - r}{h}  = 1 $$

   El producto de los factores es $$ dim = 1 \cdot 1 \cdot 1 = 1 $$ Esto corresponde a la representación singlete, que se denota simplemente por $ 1 $, ya que una representación unidimensional coincide con su conjugada, es decir, $ \bar{1} = 1 $.
4. Dos casillas en la primera fila y una en la segunda fila
   Esta configuración, aunque gráficamente distinta, tiene la misma forma que la anterior de simetría mixta y también corresponde a un octete \( 8 \).
   

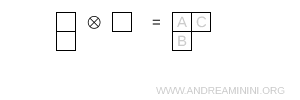
   Nota. Al tener la misma forma que el diagrama anterior, este diagrama de Young describe igualmente la representación octete ($ 8 $).

La descomposición final del producto tensorial es, por tanto:

\[ 3 \otimes 3 \otimes 3 = 10 \oplus 8 \oplus 8 \oplus 1 \]

Estos son exactamente los multipletes que se observan en el espectro experimental de los bariones.

Nota. Cada diagrama de Young no es solo una herramienta matemática, sino que tiene una interpretación física directa. El decuplete (10) describe bariones con funciones de onda de sabor completamente simétricas, como los estados \( \Delta \). El octete (8) corresponde a bariones con simetría de sabor mixta, que incluyen a los nucleones y a los bariones \( \Sigma \) y \( \Xi \). El singlete (1) representa un estado de sabor completamente antisimétrico..

Combinación de quarks: \( 3 \otimes \bar 3 \)

En este ejemplo se estudia el producto tensorial

$$ 3 \otimes \bar{3} $$

La representación fundamental \( 3 \) se representa mediante una sola casilla, mientras que la representación conjugada \( \bar{3} \) se describe con dos casillas apiladas verticalmente. Esta representación gráfica refleja su interpretación como una combinación antisimétrica de dos índices fundamentales en el grupo SU(3).

El cálculo se realiza utilizando diagramas de Young. El procedimiento consiste en añadir la casilla asociada a la representación \( 3 \) al diagrama de Young correspondiente a \( \bar{3} \). Al aplicar las reglas de SU(3), se observa que solo son admisibles dos diagramas de Young distintos.

• Dos casillas en una fila y una debajo
  Este diagrama de Young tiene forma (2,1) y dimensión 8.
  

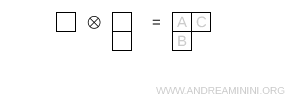
  Nota. Este caso ya se ha analizado en ejemplos anteriores. Es un resultado bien establecido que este diagrama de Young corresponde a la representación octeto \( 8 \) de SU(3).

• Tres casillas en una columna
  Este diagrama de Young tiene forma (1,1,1) y dimensión 1.
  
  
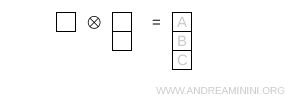
  Nota. Este caso también ha sido tratado con anterioridad. Este diagrama de Young representa la representación singlete \( 1 \) de SU(3).

La descomposición resultante es, por tanto:

$$ 3 \otimes \bar{3} = 8 \oplus 1 $$

De este modo, los diagramas de Young proporcionan una explicación clara y directa de por qué surgen determinados multipletes de sabor y de por qué no aparecen representaciones adicionales dentro de la simetría SU(3).

Combinación \( 6 \otimes \bar 3 \)

Veamos ahora cómo se evalúa el producto tensorial

$$ 6 \otimes \bar 3 $$

La representación $ 6 $ se describe mediante dos casillas colocadas en una sola fila, mientras que la representación conjugada $ \bar 3 $ se representa con dos casillas apiladas en una columna, lo que pone de manifiesto su carácter antisimétrico.

El cálculo se lleva a cabo mediante diagramas de Young. En este caso concreto, solo existe una configuración no trivial que cumple todas las reglas y, por tanto, es admisible.

• Tres casillas en la primera fila y una en la segunda
  Este diagrama de Young es de tipo (3,1) y corresponde a una representación de dimensión $ 15 $.
  
  
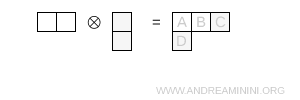
  Nota. La dimensión se obtiene mediante la fórmula estándar de la longitud del gancho \[ \dim = \prod_{\text{casillas}} \ \frac{N + c - r}{h} \], tomando $ N=3 $ en todo el cálculo.
  

  • Casilla A. El índice de fila es $ r=0 $ y el índice de columna es $ c=0 $. Hay dos casillas a la derecha y una debajo, por lo que la longitud del gancho es $ h=2+1+1=4 $ (derecha+abajo+1).  $$ \frac{N + c - r}{h} = \frac{3 + 0 - 0}{4} = \frac{3}{4} $$
  • Casilla B. El índice de fila es $ r=0 $ y el índice de columna es $ c=1 $. Hay una casilla a la derecha y ninguna debajo, de modo que $ h=1+0+1=2 $ (derecha+abajo+1).  $$ \frac{N + c - r}{h} = \frac{3 + 1 - 0}{2} = 2 $$
  • Casilla C. El índice de fila es $ r=0 $ y el índice de columna es $ c=2 $. No hay casillas ni a la derecha ni debajo, así que $ h=0+0+1=1 $ (derecha+abajo+1).  $$ \frac{N + c - r}{h} = \frac{3 + 2 - 0}{1} = 5 $$
  • Casilla D. El índice de fila es $ r=1 $ y el índice de columna es $ c=0 $. No hay casillas a la derecha ni debajo, por lo que $ h=0+0+1=1 $ (derecha+abajo+1).  $$ \frac{N + c - r}{h} = \frac{3 + 0 - 1}{1} = 2 $$

  Multiplicando todos los factores se obtiene la dimensión total $$ \dim = \frac{3}{4} \cdot 2 \cdot 5 \cdot 2 = 15 $$ Esta representación presenta una simetría mixta.
• No existen configuraciones adicionales admisibles
  Las dos casillas asociadas a la columna antisimétrica no pueden colocarse simultáneamente en una misma fila, ya que ello impondría una simetrización incompatible con la antisimetría. Tampoco pueden disponerse ambas en una columna, puesto que el diagrama inicial no contiene ninguna columna que pueda prolongarse. Si se añade solo una casilla en la fila inferior, la segunda casilla no tiene ninguna posición permitida y el canal de composición correspondiente se cierra.
  
  
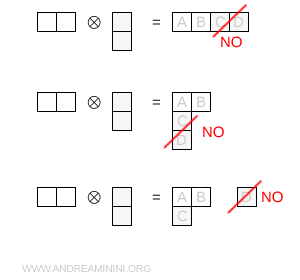
  Solución. En esta situación, la representación compatible restante se determina mediante el recuento de dimensiones. La dimensión total del producto tensorial \( 6 \otimes \bar 3 \) es \( 6 \times 3 = 18 \). Dado que ya se ha obtenido una representación de dimensión 15, el resto es $$ 18 - 15 = 3 $$ Como \( 3 \) es una representación admisible de SU(3), el término que falta en la descomposición es precisamente \( 3 \).

La descomposición final queda, por tanto,

$$ 6 \otimes \bar 3 = 15 \oplus 3 $$

De este modo, los diagramas de Young ofrecen una herramienta clara y sistemática para entender la estructura de las representaciones de SU(3) y explicar por qué ciertos multipletes aparecen de forma natural, mientras que otros no son posibles.

Y así sucesivamente.