Teoría Cuántica

La teoría cuántica fue presentada por primera vez en 1900 por el físico alemán Max Planck para explicar la distribución de la radiación electromagnética emitida por un cuerpo negro, es decir, un objeto ideal que absorbe y reemite toda la radiación incidente.

Planck propuso que la energía no se libera de manera continua, como se creía hasta entonces, sino en “paquetes” discretos llamados cuantos. La energía de cada cuanto es proporcional a la frecuencia de la radiación:

$$ E = h \cdot \nu $$

Donde $h$ es la constante de Planck.

A esta idea se la conoce como cuantización. Dicho en términos simples, un sistema físico no puede asumir cualquier valor de energía, sino únicamente múltiplos enteros de una unidad fundamental.

¿Qué significa cuantizar? Una analogía puede ser útil. Las dunas del desierto parecen olas continuas de arena, pero en realidad están formadas por una innumerable cantidad de granos individuales: unidades discretas. De la misma manera, fenómenos que parecen continuos a simple vista (como la energía de la radiación, el movimiento de los electrones o las vibraciones atómicas) resultan estar cuantizados a escala microscópica.

Una fotografía funciona de forma análoga: de lejos parece lisa y uniforme, pero al ampliarla revela una cuadrícula de puntos luminosos, los píxeles.

¿Por qué Planck introdujo el cuanto?

A comienzos del siglo XX ya se sabía que la energía emitida por un cuerpo caliente depende de su temperatura.

Para estudiarlo en condiciones ideales, los científicos definieron el concepto de cuerpo negro, un objeto que absorbe y reemite toda la radiación incidente, independientemente de su composición.

Las mediciones mostraban que, para cualquier temperatura absoluta $T$, la energía emitida $E(\lambda)$ se distribuye entre longitudes de onda $\lambda$ siguiendo una curva característica con un máximo que se desplaza a medida que cambia la temperatura.

Estas curvas presentan una típica “forma de campana”.

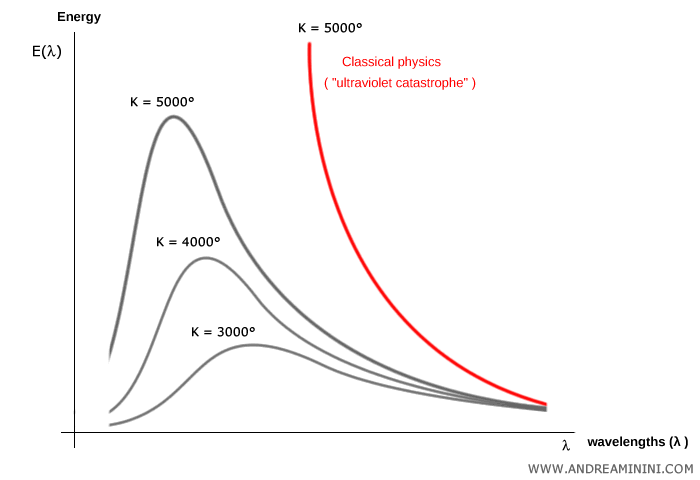
Sin embargo, la física clásica no lograba dar cuenta de este comportamiento. La teoría electromagnética predecía que un cuerpo negro debería emitir radiación de manera continua en todas las frecuencias, con una intensidad que crecería sin límite al aumentar la frecuencia.

Esto conducía a la llamada catástrofe ultravioleta: la predicción absurda de que un cuerpo negro radiaría energía infinita en las frecuencias altas.

Algunas leyes clásicas seguían siendo válidas. Por ejemplo, la ley de Stefan-Boltzmann establecía que la potencia total emitida por un cuerpo negro es proporcional a la cuarta potencia de su temperatura:

$$ E = \sigma T^4 $$

Donde $\sigma$ es la constante de Stefan-Boltzmann.

La pregunta sin resolver era cómo se distribuye la energía entre las diferentes longitudes de onda.

Para responderla, Planck propuso una idea radical: la energía electromagnética no es continua, sino que se libera en paquetes discretos, los cuantos. Aquí es donde entra en escena la constante de Planck.

¿Qué es la constante de Planck?

Si la energía está cuantizada, no puede variar de forma continua, sino solo en múltiplos enteros de una unidad fundamental.

Según Planck, la energía de la radiación electromagnética de frecuencia $\nu$ está dada por:

$$ E = h \nu $$

Donde:

• $E$ es la energía de un cuanto,
• $\nu$ es la frecuencia de la radiación,
• $h$ es la constante de Planck, aproximadamente $6.626 \times 10^{-34} \, \mathrm{J \cdot s}$.

La constante $h$ es una constante universal que define la escala mínima en la que la energía puede “empaquetarse”. No es en sí misma un cuanto, sino el factor que vincula un cuanto de energía con la frecuencia de la radiación.

De la fórmula simple a la ley de Planck

A partir de esta idea, Planck dedujo la ecuación que describe la distribución espectral de la energía emitida por un cuerpo negro:

$$ E(\nu) = \frac{8 \pi h \nu^3}{c^3} \cdot \frac{1}{e^{h\nu/kT}-1} $$

Aquí $c$ es la velocidad de la luz, $k$ la constante de Boltzmann y $T$ la temperatura absoluta.

Esta ley reproduce las curvas de emisión con forma de campana y resuelve la catástrofe ultravioleta de la física clásica.

La ley de Planck también enlaza los dos límites conocidos: la ley de Rayleigh-Jeans (bajas frecuencias) y la ley de Wien (altas frecuencias).

En síntesis, la constante de Planck marca la frontera entre la física clásica y la cuántica: por debajo de esa escala, los fenómenos dejan de ser continuos y se vuelven cuantizados.

Frecuencia y longitud de onda. La frecuencia $\nu$ y la longitud de onda $\lambda$ son dos formas de describir la misma onda: $$ c = \lambda \nu $$ La frecuencia ($\nu$) indica cuántas oscilaciones ocurren por segundo. La longitud de onda ($\lambda$) es la distancia entre dos crestas consecutivas. A mayor frecuencia, menor longitud de onda, y viceversa.

Para apreciar esta escala microscópica, pensemos en un electrón que orbita el núcleo de un átomo de hidrógeno en una trayectoria circular (2πr).

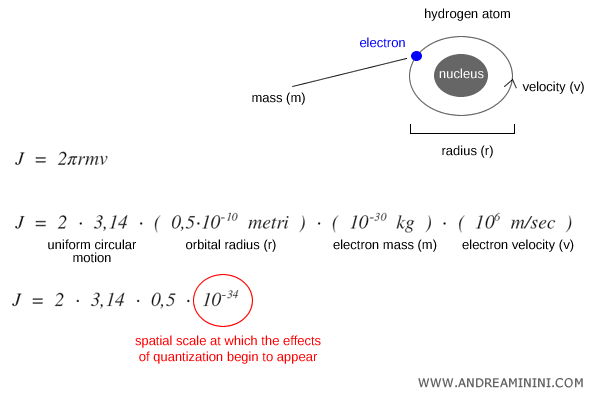
Para un electrón con masa $m \approx 9.1 \times 10^{-31}\,\text{kg}$, radio orbital $r \approx 0.5 \times 10^{-10}\,\text{m}$ y velocidad $v \approx 10^6\,\text{m/s}$, el momento angular es:

$$ J = 2 \pi r m v \sim 10^{-34} \, \text{J·s} $$

Este valor coincide con el orden de magnitud de la constante de Planck $h$.

A esta escala, la mecánica clásica deja de ser aplicable, y la cuantización de los niveles de energía (modelo de Bohr, mecánica cuántica) se vuelve esencial.

La diferencia entre cuantos y ondas electromagnéticas

En la teoría electromagnética clásica, la luz se concibe como una onda continua que reparte su energía de manera uniforme a lo largo del espectro de frecuencias.

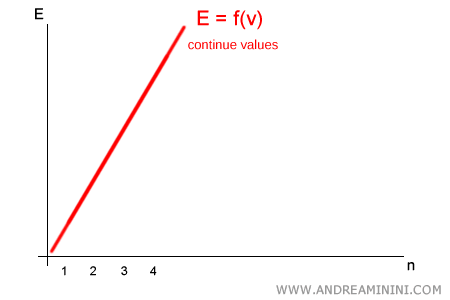
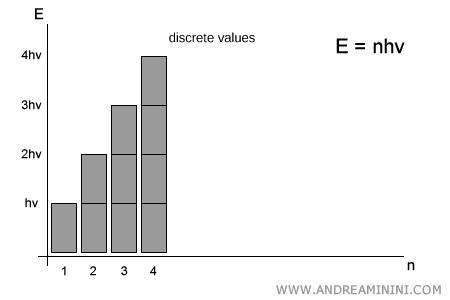
Planck, en cambio, sostuvo que la energía no es continua: solo puede adoptar valores discretos, múltiplos enteros del cuanto elemental $h\nu$. Es decir:

$$ E = n \cdot h\nu \qquad (n = 1,2,3,\dots) $$

No existen valores intermedios entre $1 \cdot h\nu$ y $2 \cdot h\nu$: un sistema solo puede emitir o absorber un número entero de cuantos.

Esta visión introdujo una nueva forma de concebir la luz: no solo como una onda, sino también como un flujo de partículas, los fotones, cada uno portador de una energía $h\nu$.

No obstante, la descripción ondulatoria no se abandonó: ambos modelos, el de onda y el de partícula, siguen siendo válidos y complementarios.

Doble naturaleza onda-partícula

Los desarrollos posteriores de la mecánica cuántica demostraron que la radiación electromagnética posee un carácter dual:

• en algunos experimentos se comporta como onda (interferencia, difracción);
• en otros se comporta como partícula (efecto fotoeléctrico, colisiones con electrones).

A esto se lo conoce como dualidad onda-partícula. Ambos aspectos coexisten y se manifiestan según el tipo de experimento.

Y este efecto no es exclusivo de la luz: electrones, protones y neutrones también muestran propiedades ondulatorias, como lo evidencian los experimentos de difracción de electrones.

El efecto fotoeléctrico

La hipótesis cuántica de Planck, formulada en 1900 para explicar la radiación del cuerpo negro, pronto se reveló esencial en otros contextos inesperados.

En 1905 Albert Einstein aplicó el concepto de cuanto al efecto fotoeléctrico, un fenómeno conocido desde finales del siglo XIX: cuando la luz incide sobre una superficie metálica, esta emite electrones.

El electromagnetismo clásico predecía que la energía transportada por la luz debía depender únicamente de su intensidad, es decir, de la amplitud de la onda.

Siguiendo esa lógica, una luz lo bastante intensa, de cualquier color, debería ser capaz de liberar electrones de un metal. Sin embargo, los experimentos mostraban lo contrario:

• Si la frecuencia de la luz ($\nu$) es demasiado baja (por ejemplo, luz roja), no se emiten electrones, por muy intenso que sea el haz.
• Si la frecuencia ($\nu$) supera un cierto umbral (como ocurre con la luz ultravioleta), incluso un haz débil expulsa electrones de manera instantánea.

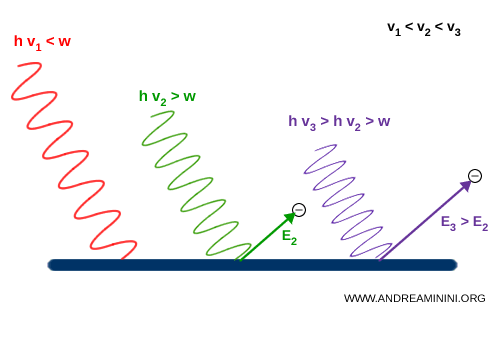
Einstein explicó este resultado proponiendo que la luz está compuesta por cuantos de energía, hoy llamados fotones, cada uno con una cantidad de energía bien definida:

$$ E = h \nu $$

Un fotón que incide sobre el metal puede transferir su energía a un electrón.

Si esa energía supera la función de trabajo $W$ (la energía mínima necesaria para liberar un electrón del metal), el electrón es emitido. De lo contrario, no ocurre nada, sin importar la intensidad de la luz.

$$ E_{kin} = h \nu - W $$

Esta explicación confirmó la naturaleza corpuscular de la radiación electromagnética junto a su carácter ondulatorio.

Nota. Por este trabajo, Einstein recibió el Premio Nobel de Física en 1921, y el efecto fotoeléctrico se convirtió en una de las pruebas decisivas de la teoría cuántica.

El modelo atómico de Bohr

En 1913 Niels Bohr propuso un nuevo modelo atómico para resolver contradicciones que la física clásica no podía explicar.

La teoría clásica predecía que un electrón en órbita alrededor del núcleo debería radiar energía de forma continua, perder velocidad, caer hacia el núcleo y hacer imposible la existencia estable de los átomos.

Bohr introdujo una idea audaz: los electrones solo pueden ocupar determinadas órbitas estacionarias que corresponden a niveles de energía discretos. En estas órbitas, los electrones no emiten energía, lo que garantiza la estabilidad del átomo.

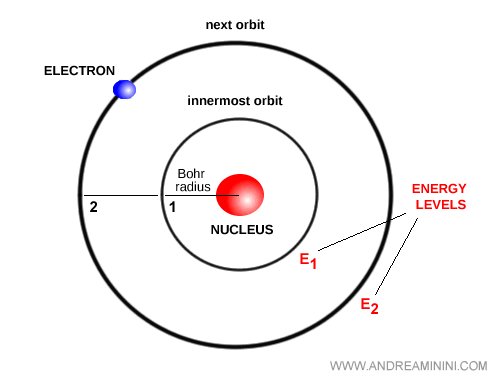
Cuando un electrón salta de un nivel a otro, el átomo emite o absorbe un fotón cuya energía es igual a la diferencia entre ambos niveles: $E = h \nu$.

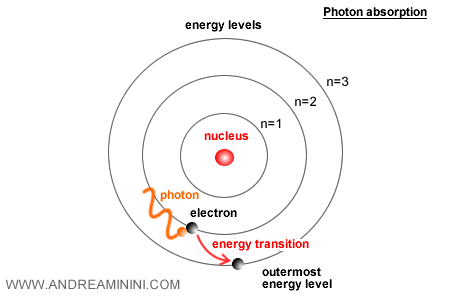
Esto permitió a Bohr explicar con gran precisión el espectro de emisión del hidrógeno, reproduciendo la secuencia de sus líneas espectrales.

La contribución de Bohr fue decisiva: incorporó el concepto de cuanto de energía (introducido por Planck y Einstein) dentro de la propia estructura atómica, marcando un paso fundamental hacia la mecánica cuántica.

De la teoría cuántica a la mecánica cuántica

En los años siguientes, la hipótesis cuántica se amplió para abarcar otros fenómenos: las ondas de materia de De Broglie (1924), la mecánica ondulatoria de Schrödinger y la mecánica matricial de Heisenberg (1925-26).

• La hipótesis de las ondas de materia de De Broglie (1924)
  Louis de Broglie propuso que no solo la luz, sino también las partículas materiales (como electrones y protones), podían presentar propiedades ondulatorias. Cada partícula con cantidad de movimiento $p$ tendría una longitud de onda asociada: $$ \lambda = \frac{h}{p} $$  Esta idea revolucionaria extendía la dualidad onda-partícula de la luz a la propia materia.
• La mecánica matricial de Heisenberg (1925)
  A partir de los datos experimentales de los espectros atómicos, Werner Heisenberg desarrolló un marco matemático basado en matrices en lugar de trayectorias o ondas visualizadas. En este enfoque, las magnitudes físicas se representan mediante operadores que obedecen reglas de conmutación específicas, dando lugar al principio de indeterminación. Poco después, Born y Jordan formalizaron el método matricial junto con Heisenberg (el trabajo Born-Jordan-Heisenberg). Aunque abstracta, esta formulación demostró ser equivalente a la de Schrödinger y contribuyó a establecer las bases de la mecánica cuántica moderna.
• La mecánica ondulatoria de Schrödinger (1926)
  Erwin Schrödinger introdujo una ecuación que describe la evolución temporal de la función de onda $\psi$, que contiene toda la información sobre el estado cuántico de un sistema. En esta visión, el electrón deja de ser una diminuta partícula en órbita y pasa a ser una onda de probabilidad extendida en el espacio. Las soluciones estacionarias de la ecuación de Schrödinger explican los niveles de energía discretos de los átomos. Su primer artículo sobre mecánica ondulatoria apareció a principios de 1926, y pronto se demostró que era matemáticamente equivalente a la mecánica matricial de Heisenberg.
• La interpretación probabilística de Born (1926)
  Max Born propuso que el cuadrado de la función de onda, $|\psi|^2$, debía interpretarse como una densidad de probabilidad. Esta interpretación otorgó a la mecánica ondulatoria un significado físico; sin ella, la teoría habría quedado como una elegante construcción matemática sin conexión con la realidad.
• El principio de indeterminación de Heisenberg (1927)
  Heisenberg formuló el principio de indeterminación ($\Delta x \cdot \Delta p \geq \hbar/2$), que puso en claro las implicaciones conceptuales de la nueva mecánica.
• Dirac y la unificación (1926-1928)
  Paul Dirac desempeñó un papel crucial al demostrar la equivalencia formal de la mecánica matricial de Heisenberg y la mecánica ondulatoria de Schrödinger. En 1928 introdujo su famosa ecuación relativista del electrón, que unificó la mecánica cuántica con la relatividad especial y predijo de manera natural la existencia de la antipartícula del electrón: el positrón, descubierto experimentalmente por Carl Anderson en 1932.
• La Conferencia Solvay (1927)
  Celebrada en Bruselas en octubre de 1927 bajo el tema “Electrones y Fotones”, estuvo dedicada a los fundamentos de la naciente mecánica cuántica. Asistieron prácticamente todos los grandes físicos de la época: Planck, Einstein, Bohr, Heisenberg, Schrödinger, Dirac, Born, Pauli, de Broglie, Lorentz y muchos otros. La famosa fotografía de grupo muestra a 29 participantes, de los cuales 17 eran o llegarían a ser premios Nobel. La Conferencia Solvay marcó el triunfo definitivo de la mecánica cuántica: las ideas de Bohr, Heisenberg, Schrödinger y Born se convirtieron en el nuevo marco de la física. Al mismo tiempo, Dirac estaba finalizando su teoría relativista del electrón (1928), completando el cuadro. A partir de entonces, la física clásica quedó restringida como una aproximación macroscópica, mientras que la física cuántica se convirtió en la descripción fundamental del mundo microscópico.

  El debate Einstein-Bohr. Einstein rechazaba la interpretación probabilística de Born, defendida con firmeza por Bohr y Heisenberg. Su célebre frase fue: “Dios no juega a los dados con el universo.” Bohr replicó que no era tarea de la física decirle a Dios lo que debía hacer, defendiendo la interpretación de Copenhague. Este debate sobre la naturaleza de la realidad cuántica se prolongaría durante décadas.

• Hacia la teoría cuántica de campos (años 1930-1940)
  Tras el desarrollo de la mecánica cuántica “no relativista”, los físicos avanzaron hacia una teoría de campos relativista. De este esfuerzo surgieron primero la mecánica cuántica relativista y luego la electrodinámica cuántica (QED). La QED trata la radiación electromagnética como un campo cuantizado y describe con extraordinaria precisión las interacciones entre electrones, positrones y fotones. Abrió el camino hacia las teorías cuánticas de las demás fuerzas fundamentales, incluida la cromodinámica cuántica (QCD) y el Modelo Estándar, y sigue siendo uno de los ejemplos más exitosos de teoría cuántica de campos.

De esta convergencia de ideas surgió la mecánica cuántica, un nuevo marco teórico que, a partir de la década de 1920, revolucionó nuestra comprensión del mundo microscópico.

La transición de la teoría cuántica a la mecánica cuántica no fue obra de una sola mente, sino el fruto de un esfuerzo colectivo en el que muchos científicos desempeñaron un papel decisivo.

Y la historia continuó.