La simetría SU(3) y la Eightfold Way de los bariones

Muchos bariones presentan propiedades físicas muy parecidas entre sí. Este hecho sugiere de manera natural que pueden describirse mediante una simetría más amplia que el isospín considerado de forma aislada. Esa simetría es SU(3), dentro de la cual ocho bariones de espín \( \tfrac12 \) se organizan en un octeto. A este esquema de clasificación se le conoce como la Eightfold Way.

La idea de simetría nace del hecho de que las leyes que gobiernan la interacción fuerte permanecen invariantes cuando se intercambian bariones con los mismos números cuánticos, diferenciándose únicamente por su posición dentro de la multipleta.

Dicho de forma sencilla, la interacción fuerte no distingue entre estos bariones. Es posible transformarlos unos en otros sin que cambie la física fundamental del sistema.

Esta invariancia se expresa de manera rigurosa mediante el grupo SU(3), que organiza los ocho bariones de espín \( \tfrac12 \) en una única representación irreducible conocida como la Eightfold Way.

Nota. La Eightfold Way fue propuesta en 1961 por el físico teórico estadounidense Murray Gell-Mann como una clasificación sistemática de los hadrones en multipletes gobernados por la simetría SU(3). En aquel momento se trataba de un marco puramente fenomenológico, basado en regularidades experimentales y sin una explicación microscópica. Solo más tarde, con la introducción del modelo de quarks en 1964, también propuesta por Gell-Mann, esta clasificación adquirió una base física sólida vinculada a la estructura interna de los hadrones.

Origen de la simetría

Durante la década de 1950 se descubrió una cantidad mucho mayor de bariones de lo que inicialmente se esperaba.

Un análisis más detallado mostró que ocho de estas partículas compartían propiedades sorprendentemente similares:

• protón \( p \)
• neutrón \( n \)
• \( \Lambda \)
• \( \Sigma^+ , \Sigma^0 , \Sigma^- \)
• \( \Xi^0 , \Xi^- \)

Todas ellas tienen espín \( \tfrac12 \), participan en la interacción fuerte y poseen masas del mismo orden de magnitud, aproximadamente entre 940 y 1320 MeV/(c²).

Este patrón indica con claridad que no se trata de partículas independientes, sino de miembros de una misma familia bariónica.

Una situación conceptualmente similar ya se había presentado en la década de 1930 con el protón y el neutrón, que resultaron estar relacionados por una simetría SU(2). El nuevo esquema era análogo, aunque involucraba ahora un conjunto más amplio de partículas.

Nota. El protón y el neutrón tienen masas casi idénticas y se diferencian principalmente por su carga eléctrica. Werner Heisenberg propuso interpretarlos como dos estados de una única partícula, el nucleón. Para formalizar esta idea se introdujo el concepto de isospín, asociado al grupo de simetría SU(2).

Con el descubrimiento de nuevos bariones surgió de manera natural la pregunta de si existía un grupo de simetría mayor que SU(2), capaz de describir simultáneamente a las ocho partículas. Este interrogante se conoció como el problema de los ocho bariones.

Gell-Mann propuso que el isospín SU(2) no es una simetría fundamental, sino un subgrupo de una simetría más amplia.

Esa simetría más general es el grupo SU(3), dentro del cual los bariones no se agrupan de forma arbitraria, sino según una estructura de simetría precisa y altamente restrictiva.

Nota. SU(3) es un grupo de Lie abstracto, análogo a SU(2), pero con ocho generadores en lugar de tres. Entre sus representaciones irreducibles destaca una de dimensión ocho, conocida como la representación octeto.

Los ocho bariones $ p, n, \Lambda, \Sigma^+, \Sigma^0, \Sigma^-, \Xi^0, \Xi^- $ forman exactamente un octeto de SU(3).

Este esquema de clasificación recibe el nombre de Eightfold Way.

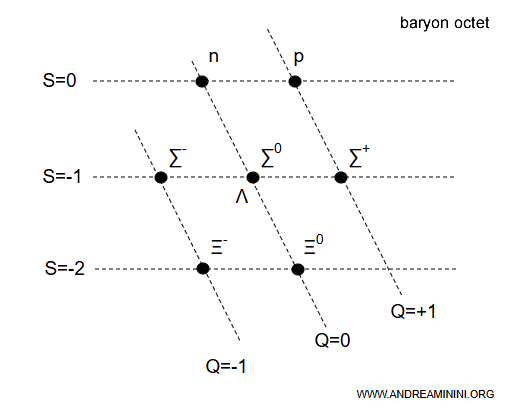
Desde este punto de vista, las ocho partículas se interpretan como estados distintos de una única representación de simetría. Esta perspectiva no solo aclara las relaciones sistemáticas entre los bariones, sino que además permite anticipar la existencia de partículas aún no observadas.

Un ejemplo emblemático es la partícula Ω⁻, cuya existencia fue predicha a partir del esquema SU(3) y confirmada posteriormente por experimentos.

De manera análoga a como \( p \) y \( n \) constituyen los dos estados de un doblete de isospín SU(2), los ocho bariones corresponden a los distintos estados de una representación de SU(3).

La Eightfold Way y el modelo de quarks

La Eightfold Way es, ante todo, un esquema de clasificación, no un modelo microscópico de la estructura interna de los hadrones.

A finales de la década de 1950 ya resultaba evidente que muchos hadrones presentaban propiedades similares y podían organizarse en multipletes gobernados por simetrías como SU(2) para el isospín y SU(3) para el sabor.

En ese momento, sin embargo, estas regularidades eran puramente empíricas. Todavía no se comprendían ni su origen físico ni la estructura interna de las partículas.

La situación cambió con la introducción del modelo de quarks por Murray Gell-Mann y, de forma independiente, por George Zweig. Este avance estableció que los hadrones no son partículas elementales, sino sistemas compuestos formados por constituyentes más fundamentales llamados quarks.

En la formulación original del modelo se introdujeron tres quarks ligeros: up (u), down (d) y strange (s).

quark	carga	isospín	extrañeza
u	\( +\tfrac23 \)	\( +\tfrac12 \)	0
d	\( -\tfrac13 \)	\( -\tfrac12 \)	0
s	\( -\tfrac13 \)	0	-1

Estos tres quarks \( (u, d, s) \) forman la representación fundamental triplete de SU(3), que constituye el elemento estructural central del modelo.

La simetría de sabor SU(3) relaciona a los quarks \( u \), \( d \) y \( s \), tratándolos como equivalentes frente a la interacción fuerte, salvo por las diferencias en sus masas. A partir de estos constituyentes fundamentales puede entenderse de manera unificada el espectro y las propiedades de los hadrones.

En particular, los bariones están formados por tres quarks:

$$ qqq $$

La combinación de tres representaciones triplete de SU(3) conduce a:

$$ 3 \otimes 3 \otimes 3 = 10 \oplus 8 \oplus 8 \oplus 1 $$

Esta descomposición explica el espectro bariónico observado:

• 10 corresponde al decuplete de bariones con espín \( \tfrac32 \)
• 8 corresponde al octeto de bariones con espín \( \tfrac12 \)
• 1 corresponde a un estado singlete

En consecuencia, la existencia del decuplete y del octeto de bariones no es una hipótesis arbitraria, sino una consecuencia matemática directa de la simetría de sabor SU(3).

Como ejemplo concreto, el octeto de bariones puede describirse explícitamente en términos de su contenido en quarks. Está formado por ocho bariones construidos a partir de los quarks \( (u, d, s) \):

Barión	composición
p	uud
n	udd
\( \Lambda \)	uds
\( \Sigma^+ \)	uus
\( \Sigma^0 \)	uds
\( \Sigma^- \)	dds
\( \Xi^0 \)	uss
\( \Xi^- \)	dss

Este patrón no es casual. La simetría de sabor SU(3) resulta especialmente eficaz porque los bariones están formados por tres quarks tomados del conjunto \( (u, d, s) \).

Desde este punto de vista, el modelo de quarks proporciona el fundamento microscópico de la Eightfold Way al introducir los quarks \( (u, d, s) \), que constituyen la representación triplete fundamental de SU(3).

Al combinar estos tres quarks, los multipletes bariónicos que originalmente se identificaron de forma empírica dentro del esquema de la Eightfold Way emergen de manera natural como consecuencia directa de la estructura de simetría subyacente.

Nota. La simetría de sabor SU(3) no es exacta, ya que las masas de los quarks no son iguales: $$ m_u \approx m_d \ll m_s $$ En consecuencia, SU(3) es solo una simetría aproximada. La presencia de la extrañeza rompe la simetría, aunque la estructura global de los multipletes sigue siendo claramente reconocible. En cambio, la simetría de isospín SU(2) suele ser considerablemente más precisa.

El decuplete de bariones

Tras la identificación del octete de bariones con espín \( \tfrac12 \), la evidencia experimental reveló la existencia de otros bariones con propiedades muy similares, pero con un espín total distinto, concretamente \( \tfrac32 \).

Estos nuevos estados no encajaban dentro del octete conocido. Sin embargo, su notable regularidad mostraba con claridad que no se trataba de fenómenos aislados ni accidentales.

Todo ello puso de manifiesto que la simetría SU(3) es más rica y profunda de lo que se había pensado inicialmente.

Un análisis cuidadoso de las configuraciones permitidas por la estructura matemática de SU(3) muestra que, además del octete (8), aparecen de forma natural otras representaciones irreducibles, entre ellas un decuplete (10) y un singlete (1):

\[ 3 \otimes 3 \otimes 3 = 10 \oplus 8 \oplus 8 \oplus 1 \]

Esta descomposición no es una hipótesis física, sino una consecuencia directa y rigurosa de la teoría de representaciones.

Nota. En otras palabras, si existe el octete, entonces el decuplete también debe existir, ya que ambos surgen inevitablemente de la misma estructura matemática subyacente.

El decuplete de bariones describe estados completamente simétricos en el espacio de sabores y, por tanto, corresponde a bariones con espín total \( \tfrac32 \).

A diferencia del octete, que adopta una disposición hexagonal con un estado central, el decuplete se organiza en forma de triángulo equilátero, compuesto por diez estados distribuidos en cuatro niveles bien definidos.

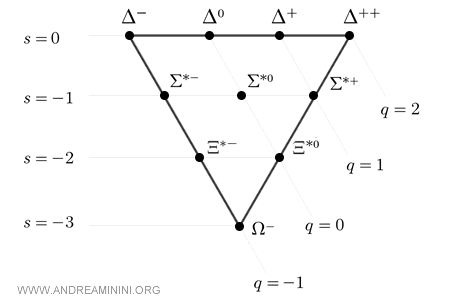
Nota. La forma triangular no es solo un recurso visual. Refleja una estructura física profunda: todas las partículas del decuplete tienen sus espines alineados, lo que da lugar a un espín total de \( \tfrac32 \), y la simetría entre los quarks alcanza su grado máximo.

El diagrama se construye organizando las partículas según dos números cuánticos fundamentales: la extrañeza ( $ S $ ) y la carga eléctrica ( $ Q $ ).

A medida que se desciende en el diagrama, la extrañeza disminuye, lo que indica un número creciente de quarks extraños en la composición de cada partícula.

En el vértice superior del triángulo se encuentran cuatro bariones \( \Delta \), que no contienen quarks extraños y están formados exclusivamente por quarks up (u) y down (d).

• \( \Delta^{++} = uuu \)
• \( \Delta^+ = uud \)
• \( \Delta^0 = udd \)
• \( \Delta^- = ddd \)

Justo por debajo aparecen tres bariones \( \Sigma \), cada uno formado por un quark extraño (s) y dos quarks ligeros, up (u) y down (d):

• \( \Sigma^{*+} = uus \)
• \( \Sigma^{*0} = uds \)
• \( \Sigma^{*-} = dds \)

La presencia de un quark extraño rompe ligeramente la simetría y se traduce en un aumento de la masa con respecto a los bariones \( \Delta \).

Nota. El asterisco indica que la partícula \( \Sigma \) se encuentra en un estado de espín \( \tfrac32 \). Pertenece a la misma familia de bariones \( \Sigma \) que aparece en el octete, pero se presenta en una configuración de espín diferente. En este caso, el espín total deja de ser \( \tfrac12 \) y pasa a ser \( \tfrac32 \), porque los espines de los tres quarks constituyentes están completamente alineados (↑↑↑). \[ \tfrac12 + \tfrac12 + \tfrac12 = \tfrac32 \] Esta configuración es precisamente la que caracteriza a los estados del decuplete. En cambio, cuando los espines no están todos alineados (↑↑↓, ↑↓↑ o ↓↑↑), su combinación vectorial da lugar a un espín total menor: \[ \tfrac12 + \tfrac12 - \tfrac12 = \tfrac12 \] En este caso, el estado resultante tiene espín \( \tfrac12 \) y pertenece al octete bariónico. Por tanto, la diferencia entre \( \Sigma \) y \( \Sigma^* \) no reside en su contenido en quarks, que es exactamente el mismo, sino únicamente en la forma en que se acoplan sus espines. El mismo razonamiento se aplica a la partícula \( \Xi^* \), que representa la versión de espín \( \tfrac32 \) del correspondiente barión \( \Xi \) del octete.

En el nivel siguiente aparecen dos bariones \( \Xi \), formados por dos quarks extraños y un quark ligero. Sus masas son aún mayores.

• \( \Xi^{*0} = uss \)
• \( \Xi^{*-} = dss \)

Finalmente, en la base del triángulo se encuentra una única partícula, el \( \Omega^- \), compuesta exclusivamente por quarks extraños:

\[ \Omega^- = sss \]

Esta partícula representa el nivel inferior del decuplete y se caracteriza por una extrañeza de -3, una carga eléctrica de -1 y un espín de \( \tfrac32 \).

La predicción de la partícula \( \Omega^- \)

El mayor logro de este marco teórico fue la predicción de la partícula \( \Omega^- \).

Esta partícula ocupa el vértice inferior del decuplete y completa la estructura simétrica anticipada por la teoría, a pesar de que aún no había sido observada en el momento en que se formuló el modelo.

Cuando finalmente fue descubierta de forma experimental en 1964, proporcionó una confirmación contundente de la validez de la simetría de sabor SU(3).

Y así sucesivamente.