Fotones

El fotón es la partícula elemental que constituye el cuanto del campo electromagnético. 

En la teoría cuántica de campos, el fotón actúa como portador de la interacción electromagnética, de la misma manera que el gluón transmite la fuerza fuerte y los bosones $ W $ y $ Z $ median la fuerza débil.

El fotón carece de masa en reposo y de carga eléctrica. Posee espín 1, por lo que se clasifica como un bosón vectorial.

Siempre se desplaza a la velocidad de la luz en el vacío, $ c = 299{,}792{,}458 \ m/s $, y todos los fotones con la misma energía son indistinguibles entre sí.

Dualidad onda-partícula

Los fotones manifiestan una doble naturaleza:

• Ondulatoria, evidente en fenómenos como la interferencia, la difracción y la polarización.
• Corpuscular, observable en el efecto fotoeléctrico, la dispersión Compton y la radiación de cuerpo negro.

Esta dualidad está en el corazón de la mecánica cuántica y da forma al principio de complementariedad: el fotón no es “onda o partícula”, sino ambas cosas a la vez, según cómo se lo observe.

Energía y momento

La energía de un fotón es directamente proporcional a su frecuencia $\nu$, de acuerdo con la relación fundamental:

$$ E = h \nu $$

Aquí $h$ es la constante de Planck, $ h \approx 6{,}626 \times 10^{-34} \ \text{J·s} $, y $\nu$ corresponde a la frecuencia de la radiación.

Aun sin tener masa en reposo, el fotón transporta una cantidad de movimiento dada por:

$$ p = \frac{E}{c} = \frac{h\nu}{c} = \frac{h}{\lambda} $$

donde $\lambda$ es la longitud de onda.

El origen del concepto de fotón

El fotón no fue descubierto en un único experimento; más bien, su concepción se fue gestando de manera progresiva entre 1900 y 1924.

Planck y la cuantización de la radiación (1900)

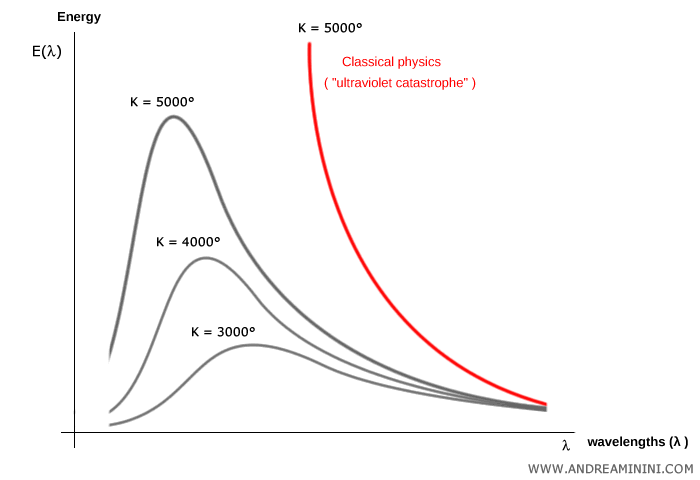
Al estudiar la radiación del cuerpo negro, Max Planck propuso que la energía electromagnética no se emitía de forma continua, sino en paquetes discretos denominados cuantos:

$$ E = h\nu $$

donde $E$ es la energía de la radiación electromagnética, $\nu$ su frecuencia y $ h \approx 6{,}626 \times 10^{-34} \ \text{J·s} $ la constante de Planck.

Dicho de otro modo, la energía de un fotón es proporcional a su frecuencia $\nu$ y solo puede adoptar valores discretos, múltiplos de $h\nu$:

$$ E = n h \nu \quad \text{con} \quad n = 1, 2, 3, \dots $$

Aquí $n$ es un número entero positivo que indica cuántos cuantos de energía están involucrados. Esta unidad elemental, $h\nu$, es el cuanto de energía. La radiación, por tanto, no se emite ni se absorbe de manera continua, sino en “saltos” discretos. A partir de esta hipótesis, Planck dedujo una nueva expresión para la densidad espectral de la radiación, conocida hoy como la ley de Planck:

$$ \rho(\nu, T) = \frac{8 \pi \nu^2}{c^3} \cdot \frac{h\nu}{e^{h\nu/(kT)} - 1} $$

En esta ecuación, $h\nu$ es la energía de un fotón. Para frecuencias bajas ($h\nu \ll kT$) se recupera la ley clásica de Rayleigh-Jeans, mientras que a frecuencias altas ($h\nu \gg kT$) la radiación decrece de manera exponencial, evitando la catástrofe ultravioleta. Este resultado fue la primera evidencia clara de la cuantización en física y marcó el nacimiento de la teoría cuántica. Es importante subrayar que el propio Planck no interpretó esta idea como una propiedad intrínseca de la naturaleza, sino como un artificio matemático para reconciliar la teoría con los experimentos.

Einstein y el efecto fotoeléctrico (1905)

Einstein partió de un hecho experimental bien conocido: al iluminar un metal con luz ultravioleta, o con luz de frecuencia suficientemente alta, se observa que de su superficie se desprenden electrones.

A este fenómeno se lo denomina efecto fotoeléctrico.

Los electrones liberados se proyectan hacia el exterior como si la luz los golpeara y los arrancara del metal.

En 1905, Einstein ofreció una interpretación audaz: la luz no solo se comporta como onda, sino que está formada por cuantos discretos de energía, a los que hoy llamamos “fotones”. Cada fotón transporta una energía determinada por:

$$ E = h \nu $$

donde $h$ es la constante de Planck y $\nu$ la frecuencia de la radiación.

Cuando un fotón impacta sobre un electrón en el metal, le transfiere toda su energía ($h\nu$). Una parte de esa energía se emplea en superar la llamada “función de trabajo” ($w$), que mantiene al electrón ligado al metal, y el resto se manifiesta como energía cinética del electrón:

$$ E_{\text{cinética}} \leq h\nu - w $$

Einstein señaló que si la frecuencia es demasiado baja, ningún electrón puede liberarse, por más que aumente la intensidad de la luz:

$$ w > h\nu $$

En cambio, cuando la frecuencia $\nu$ supera el umbral fijado por la función de trabajo, los electrones son efectivamente emitidos:

$$ w \leq h\nu $$

A frecuencias más altas, la energía cinética de los electrones expulsados aumenta. La intensidad de la luz solo determina la cantidad de electrones liberados, pero no la energía individual de cada uno.

Ejemplo. Con una radiación de frecuencia $ \nu_1 $ (roja), la frecuencia resulta demasiado baja y no se expulsa ningún electrón. Con una radiación de frecuencia $ \nu_2 $ (verde), la frecuencia apenas alcanza el umbral y los electrones se emiten con energía cinética $ E_2 $. Con una radiación de frecuencia $ \nu_3 $ (violeta), la frecuencia es aún mayor y los electrones salen con una energía superior: $ E_3 > E_2 $.

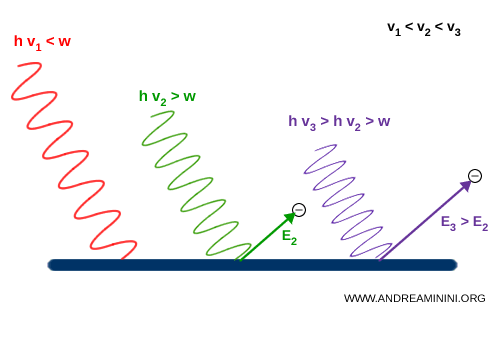
Einstein comprendió que la energía de los electrones fotoemitidos depende exclusivamente de la frecuencia de la luz, no de su intensidad.

Una idea sencilla en apariencia, pero tan disruptiva que transformó para siempre el rumbo de la física moderna.

Nota. La hipótesis de Einstein fue inicialmente recibida con escepticismo, ya que evocaba la antigua teoría corpuscular de la luz de Newton, considerada superada. Incluso Robert Millikan, quien confirmó experimentalmente la ecuación de Einstein, se resistió durante años a aceptar sus consecuencias conceptuales. Solo tras casi dos décadas y numerosas comprobaciones experimentales, la comunidad científica terminó por reconocer plenamente la existencia del fotón.

El experimento de Compton (1923)

En 1923, Arthur Compton ofreció una confirmación definitiva de la naturaleza corpuscular de la luz al medir el desplazamiento en la longitud de onda de los rayos X dispersados:

$$ \lambda' = \lambda + \lambda_c(1 - \cos\theta) $$

donde $ \lambda_c $ es la longitud de onda de Compton.

Este fenómeno, explicado como una colisión elástica relativista, constituyó la prueba concluyente de que los fotones poseen tanto energía como cantidad de movimiento.

Nota. El término “fotón” fue introducido poco después, en 1926, por Gilbert Lewis.

El fotón en la Teoría Cuántica de Campos (QFT)

La teoría cuántica de campos sustituyó la visión clásica de un campo continuo por la de un campo cuantizado. En este marco, el campo electromagnético está compuesto por cuantos discretos: los fotones.

Las fuerzas dejan de entenderse como influencias continuas que se propagan en el espacio y se interpretan, en cambio, como intercambios de partículas mediadoras entre cargas.

En el caso del electromagnetismo, los mediadores son los fotones, que actúan como mensajeros cuánticos capaces de producir tanto atracción como repulsión, según la interacción.

Por ejemplo, la repulsión entre dos electrones puede describirse como el intercambio constante de fotones virtuales que transmiten la fuerza.

En síntesis, la idea del fotón nació como una hipótesis matemática propuesta por Planck, fue reinterpretada y fundamentada por Einstein, y alcanzó su confirmación experimental definitiva con el experimento de Compton.

Su doble carácter -onda y partícula a la vez- solo adquiere pleno sentido dentro de la teoría cuántica de campos, donde el fotón se reconoce como el cuanto del campo electromagnético y el mediador de sus interacciones.

El fotón en la física cuántica

En la física clásica, dos cargas eléctricas (por ejemplo, dos electrones) se repelen porque cada una genera un campo que actúa sobre la otra.

En la descripción cuántica, en cambio, la interacción se entiende como un intercambio continuo de fotones, como si las cargas se enviaran sin cesar estas partículas mediadoras encargadas de transmitir la fuerza de atracción o de repulsión.

Precaución. No hay que imaginar estos mediadores -los fotones- como pequeñas bolitas que rebotan de un lado a otro. Los fotones virtuales pueden explicar tanto la atracción como la repulsión, y su papel es más sutil que cualquier analogía mecánica.

En los átomos, por ejemplo, los electrones permanecen ligados al núcleo gracias a la atracción de los protones cargados positivamente. En el lenguaje cuántico, esta interacción se explica mediante el intercambio permanente de fotones virtuales entre electrones y protones.

De forma análoga, dos electrones se repelen por tener la misma carga, lo que también se describe como un intercambio de fotones virtuales.

Este enfoque se extiende a todas las interacciones fundamentales:

• Interacción electromagnética: dos electrones se repelen al intercambiar fotones virtuales, mediadores de la fuerza electromagnética.
• Interacción débil: en la desintegración beta, un neutrón se convierte en un protón emitiendo un $W^-$, que luego se desintegra en un electrón y un antineutrino.
• Interacción fuerte: los quarks dentro de protones y neutrones permanecen unidos gracias al intercambio de gluones, que actúan como el “pegamento” del núcleo.
• Gravedad: según la teoría, las masas se atraen intercambiando gravitones, partículas hipotéticas aún no observadas.

Nota. En numerosos contextos, la física clásica sigue siendo una excelente aproximación -por ejemplo, la ley de Coulomb en el caso del campo eléctrico-. Esto se debe a que, en sistemas estables como los átomos, el intercambio de una cantidad enorme de fotones virtuales hace que el campo se perciba como prácticamente continuo y los efectos cuánticos resulten despreciables. No obstante, en fenómenos como el efecto fotoeléctrico o la dispersión Compton, la naturaleza cuántica de la luz se manifiesta de manera inconfundible. En tales situaciones, la estructura discreta del campo se vuelve esencial y los fotones deben entenderse como verdaderas partículas: cuantos de energía que van más allá de cualquier modelo de campo continuo.

Y la historia continúa...