La Vía Óctuple
La Vía Óctuple es un sistema de clasificación de partículas subatómicas que organiza bariones y mesones en familias con propiedades comunes, utilizando dos números cuánticos esenciales:
- Carga eléctrica $Q$
- Extrañeza $S$, número cuántico que señala la presencia de quarks extraños o antiquarks en la partícula.
Fue propuesta en 1961 por Murray Gell-Mann y, de forma independiente, por Yuval Ne’eman, tomando como base el grupo de simetría matemática SU(3).
La Vía Óctuple buscaba poner orden en el llamado “zoológico de partículas” de las décadas de 1950 y 1960, cuando se habían descubierto decenas de partículas sin un marco coherente que permitiera organizarlas.
Estas agrupaciones suelen representarse mediante figuras geométricas regulares, como hexágonos y triángulos.
Ejemplo
En el caso de los bariones, la extrañeza $S$ se representa en el eje vertical, mientras que la carga eléctrica $Q$ aparece en los ejes diagonales.
A esta disposición se la conoce como el octete de bariones.
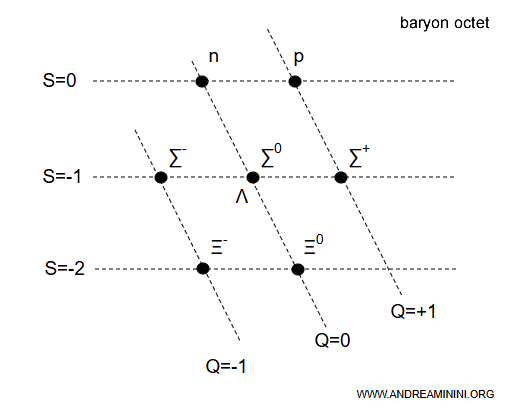
Recibe el nombre de “octete” porque este diagrama hexagonal contiene ocho bariones.
Nota. En este diagrama, los bariones -partículas con espín $ \frac{1}{2} $ formadas por tres quarks- se disponen de acuerdo con su extrañeza ($S$, eje vertical) y su carga eléctrica ($Q$, eje horizontal).
- En la parte superior, con $S = 0$, se encuentran el neutrón $n$ (neutro, $Q = 0$) y el protón $p$ (carga positiva, $Q = +1$).
- En $S = -1$ aparecen los tres bariones $\Sigma$ ($\Sigma^{+}$, $\Sigma^{0}$, $\Sigma^{-}$), junto con el barión $\Lambda$ ($Q = 0$).
- En la parte inferior, con $S = -2$, están los bariones $\Xi$, cada uno con dos quarks extraños $s$. El $ \Xi^{-} = (d s s) $ posee carga negativa ($Q = -1$), mientras que el $ \Xi^{0} = (u s s) $ es neutro ($Q = 0$).
Un esquema hexagonal análogo se utiliza para los mesones.
Este es el octete de mesones:
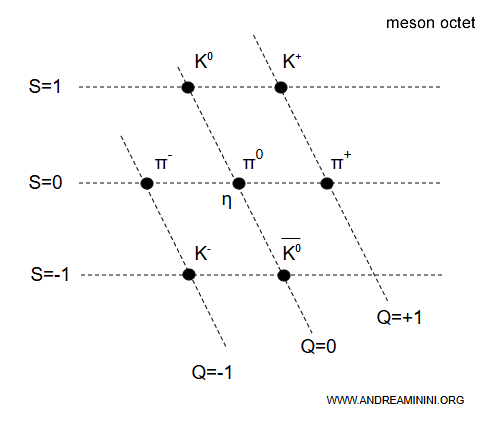
En este caso, la fila superior corresponde a $S = +1$ y la inferior a $S = -1$, es decir, el orden inverso al de los bariones.
Nota. Este diagrama muestra mesones pseudosescalares -partículas compuestas por un quark y un antiquark- organizados según su extrañeza ($S$, eje vertical) y su carga eléctrica ($Q$, eje horizontal).
- En la parte superior, con $S = +1$, se ubican el kaón neutro $K^{0}$ ($Q = 0$) y el kaón positivo $K^{+}$ ($Q = +1$).
- En $S = 0$ aparecen los tres piones ($\pi^{-}$, $\pi^{0}$, $\pi^{+}$) junto con el mesón $\eta$.
- En la parte inferior, con $S = -1$, se encuentran el kaón negativo $K^{-}$ ($Q = -1$) y el antikaón neutro $\overline{K}^{0}$ ($Q = 0$). Esta disposición refleja la simetría de sabor $SU(3)$, que agrupa estos mesones en un octete de acuerdo con sus números cuánticos.
Estas agrupaciones fueron clave para establecer la primera clasificación sistemática de las partículas extrañas, incorporando el número cuántico de “extrañeza” introducido en los años cincuenta.
El esquema incluso permitió predecir partículas hasta entonces desconocidas -la más famosa, el $ \Omega^- $ (carga $-1$, extrañeza $-3$), descubierta en 1964.
Sin embargo, el modelo también tiene limitaciones.
Nota. La simetría es solo aproximada, y las masas de las partículas dentro de un mismo multiplete no son idénticas. Además, el modelo no explica por qué las partículas poseen masas concretas ni por qué interactúan de la manera en que lo hacen.
Aun así, representó un avance decisivo en la clasificación de partículas y abrió el camino hacia el modelo de quarks, en el que los bariones del octete y del decuplete se entienden como combinaciones de tres quarks ($u$, $d$, $s$).
Decuplete bariónico
Tras la identificación del octete bariónico con espín \( \tfrac12 \), los físicos descubrieron rápidamente la existencia de otras partículas con propiedades muy similares, pero con un espín intrínseco mayor, igual a \( \tfrac32 \).
Estos nuevos estados no podían encajarse dentro del octete conocido. Sin embargo, la regularidad con la que aparecían reveló que no se trataba de casos aislados, sino de la manifestación de una estructura más profunda y altamente organizada, gobernada por la simetría SU(3).
Desde el punto de vista matemático, la combinación de tres quarks en la representación fundamental de SU(3) conduce a la descomposición
$$ 3 \otimes 3 \otimes 3 = 10 \oplus 8 \oplus 8 \oplus 1 $$
En esta expresión, la representación $ 10 $ corresponde al decuplete, $ 8 $ al octete y $ 1 $ a un singlete.
En otras palabras, la existencia del octete implica de forma natural la del decuplete, ya que ambos surgen de la misma estructura de simetría subyacente.
El decuplete bariónico está formado por estados completamente simétricos en el espacio de sabores. Como consecuencia directa de esta simetría máxima, todas las partículas del decuplete poseen un espín total igual a \( \tfrac32 \).
A diferencia del octete, que adopta una disposición hexagonal con un estado central, el decuplete se organiza en forma de triángulo equilátero, compuesto por diez estados distribuidos en cuatro niveles.
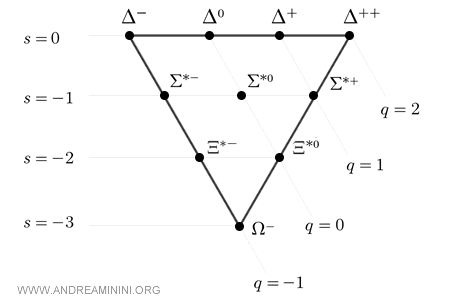
Nota. La geometría triangular no es una elección puramente gráfica. Refleja una propiedad física profunda: en el decuplete, los espines de los quarks están completamente alineados, lo que conduce a un espín total de \( \tfrac32 \) y a una simetría interna máxima.
El diagrama del decuplete se construye a partir de dos números cuánticos fundamentales: la extrañeza \( S \) y la carga eléctrica \( Q \). Al descender en el diagrama, la extrañeza disminuye progresivamente, mientras aumenta el número de quarks extraños.
En la parte superior del triángulo se encuentran cuatro partículas \( \Delta \), que no contienen quarks extraños y están formadas exclusivamente por quarks up \( u \) y down \( d \).
- \( \Delta^{++} = uuu \)
- \( \Delta^{+} = uud \)
- \( \Delta^{0} = udd \)
- \( \Delta^{-} = ddd \)
Justo por debajo aparecen tres partículas \( \Sigma \), cada una con un quark extraño \( s \) y dos quarks ligeros. La presencia del quark extraño rompe la simetría y se traduce en un aumento de la masa con respecto a los estados \( \Delta \).
- \( \Sigma^{*+} = uus \)
- \( \Sigma^{*0} = uds \)
- \( \Sigma^{*-} = dds \)
Nota. El asterisco indica un estado con espín \( \tfrac32 \). La diferencia entre \( \Sigma \) y \( \Sigma^{*} \) no reside en su contenido en quarks, que es idéntico, sino en la forma en que se combinan sus espines. Cuando todos los espines están alineados (↑↑↑), el espín total es \[ \tfrac12 + \tfrac12 + \tfrac12 = \tfrac32 \] Cuando no están completamente alineados (↑↑↓, ↑↓↑, ↓↑↑), el resultado es \[ \tfrac12 + \tfrac12 - \tfrac12 = \tfrac12 \] y el estado pertenece al octete. El mismo razonamiento se aplica a los bariones \( \Xi^{*} \).
En el nivel siguiente aparecen dos partículas \( \Xi \), cada una formada por dos quarks extraños y un quark ligero. Como consecuencia, sus masas son mayores.
- \( \Xi^{*0} = uss \)
- \( \Xi^{*-} = dss \)
En la base del triángulo se encuentra una única partícula, el \( \Omega^{-} \), formada exclusivamente por quarks extraños:
$$ \Omega^{-} = sss $$
Esta partícula ocupa el nivel inferior del decuplete y se caracteriza por presentar extrañeza \( S = -3 \), carga eléctrica \( Q = -1 \) y espín \( \tfrac32 \).
La predicción del \( \Omega^{-} \). Uno de los mayores logros del modelo de quarks fue la predicción del \( \Omega^{-} \). Este estado completa la estructura simétrica del decuplete y, en el momento de su formulación teórica, aún no había sido observado experimentalmente. Su descubrimiento en 1964 constituyó una confirmación decisiva de la simetría SU(3) y del poder predictivo del modelo de quarks.
Y más allá.