Leyes de conservación en la física subatómica
Una ley de conservación es un principio fundamental de la física que establece que ciertas magnitudes esenciales - como la energía, el momento lineal, la carga eléctrica o el número bariónico - permanecen invariantes en todo proceso natural, independientemente de las transformaciones que tengan lugar en el sistema.
En pocas palabras, estas magnitudes pueden cambiar de forma o redistribuirse entre las partículas involucradas, pero el valor total antes y después de cualquier interacción se mantiene constante. Todo proceso físico debe respetar estos principios de conservación.
Estas leyes constituyen la piedra angular de la física de partículas: determinan qué reacciones son posibles, qué desintegraciones ocurren realmente y cuáles están completamente excluidas.
Ejemplo. En el decaimiento beta, un neutrón se transforma en un protón, un electrón y un antineutrino electrónico: $$ n \;\to\; p^+ + e^- + \bar{\nu}_e $$ El neutrón posee carga eléctrica nula. Tras el decaimiento, el protón tiene +1, el electrón -1 y el neutrino 0. El resultado es $+1-1+0 = 0$, por lo que la carga inicial del neutrón queda conservada. $$ n^{(0)} \;\to\; p^{+(+1)} + e^{(-1)} + \bar{\nu}_e^{(0)} $$
Algunas de estas leyes de conservación son absolutas, como la de la carga eléctrica, el número bariónico o la energía.
Otras solo se cumplen bajo ciertas condiciones, como la conservación del sabor o la regla OZI, que explican por qué algunos decaimientos son extremadamente raros o prácticamente inexistentes.
Leyes de conservación en las interacciones fundamentales
Estas son las principales leyes de conservación que rigen el comportamiento de las partículas elementales:
- Conservación de la carga eléctrica
La suma de las cargas de las partículas iniciales debe coincidir con la de las partículas finales. Esta ley es universal y se cumple en todas las interacciones fundamentales: fuerte, electromagnética y débil.Ejemplo: En un vértice de interacción débil, $$ \nu_e \to e^- + W^+ $$ la carga inicial es 0 (del neutrino), mientras que la final corresponde al electrón ( -1) más la del bosón $W^+$ (+1), resultando -1 + +1 = 0. El balance se cumple: la carga se conserva.
- Conservación del color (QCD)
En las interacciones fuertes, el color de los quarks (rojo, verde, azul) puede variar, pero el gluón transporta siempre la diferencia. Como todas las partículas observables son neutras en color (blancas), la regla es clara: entra cero, sale cero. Ninguna partícula aislada puede existir con una carga de color sin compensar.Ejemplo. Un protón está formado por tres quarks (rojo + verde + azul): $$ u_r + u_g + d_b $$ Si uno de los quarks cambia de color al emitir un gluón, este se lleva la diferencia, garantizando que el protón como conjunto permanezca incoloro.
- Conservación del número bariónico
El número bariónico total permanece constante en toda interacción. Cada quark aporta +1/3, cada antiquark -1/3. Así, los bariones (tres quarks) tienen número bariónico +1, los antibariones (tres antiquarks) -1 y los mesones (pares quark-antiquark) 0. Los bariones y antibariones nunca aparecen ni desaparecen de manera aislada: siempre se crean o destruyen en pares. Esta es una de las leyes más firmes, jamás observada en violación, y sustenta la estabilidad del protón.Ejemplo. Esta reacción respeta la conservación del número bariónico: $$ p + \bar{p} \;\to\; \pi^+ + \pi^- $$ El protón (p) tiene número bariónico +1, el antiprotón -1, mientras que los piones poseen 0. Tanto el estado inicial como el final suman 0. $$ p^{(+1)} + \bar{p}^{(-1)} \;\to\; \pi^{+(0)} + \pi^{-(0)} $$ El número bariónico queda conservado.
- Conservación de los números leptónicos
Existen tres números leptónicos independientes: el electrónico $L_e$, el muónico $L_\mu$ y el tauónico $L_\tau$. Cada uno se conserva por separado en las interacciones fundamentales, salvo en las oscilaciones de neutrinos, donde un tipo puede transformarse en otro. Solo los leptones poseen número leptónico; todas las demás partículas tienen cero. Por ejemplo, $L_e$ es +1 para el electrón y el neutrino electrónico, y -1 para sus antipartículas.
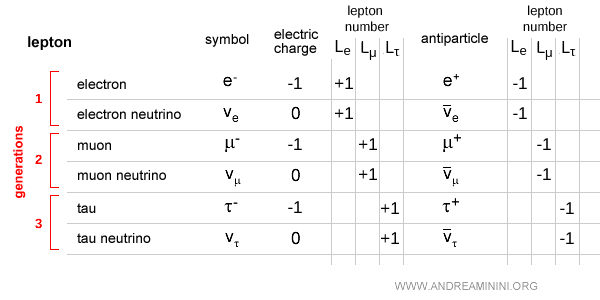
Los quarks, en cambio, no siguen una ley estricta de conservación por generaciones, ya que las interacciones débiles mezclan de forma natural los sabores de los quarks mediante la matriz CKM.Ejemplo. Un caso clásico es el decaimiento del pión cargado: $$ \pi^- \;\to\; \mu^- + \bar{\nu}_\mu $$ Asignando números leptónicos: $$ \pi^{- (0)} \;\to\; \mu^{- (L_\mu = +1)} + \bar{\nu}_\mu^{(L_\mu = -1)} $$ La suma inicial es $0$, y la final $+1 + (-1) = 0$. El número leptónico muónico $L_\mu$ se conserva.
- Conservación aproximada del sabor
La conservación del sabor no es universal; depende de la interacción:- En las interacciones fuerte y electromagnética, los sabores de los quarks (up, down, strange, charm, bottom, top) se conservan estrictamente.
- En las interacciones débiles, en cambio, los sabores pueden cambiar: un quark puede transformarse en otro ($u \to d$, $s \to u$, etc.).
Ejemplo. En las interacciones fuertes, las partículas extrañas se generan siempre en pares $s$ - $\bar{s}$, manteniendo la extrañeza total. En los decaimientos, sin embargo, un quark extraño puede cambiar de sabor gracias a la interacción débil, lo que explica que los decaimientos de partículas extrañas sean comparativamente lentos.
- Regla OZI (Okubo - Zweig - Iizuka)
Algunos decaimientos que son cinemáticamente posibles resultan extraordinariamente raros. Esto sucede cuando el diagrama de Feynman del proceso puede “cortarse” en dos partes separando únicamente líneas de gluones (sin cortar líneas de partículas reales). En esos casos, el decaimiento no está estrictamente prohibido, pero sí fuertemente suprimido: la probabilidad de que ocurra es prácticamente nula.
Junto a estas leyes, están las más “evidentes” leyes cinemáticas de la física:
- Conservación de la energía
La energía total de un sistema aislado no puede aumentar ni disminuir; solo puede transformarse de una forma a otra. - Conservación del momento lineal
En ausencia de fuerzas externas, el momento lineal total de un sistema se mantiene constante, aunque las partículas cambien de dirección o velocidad. - Conservación del momento angular
Si no actúan torques externos sobre el sistema, el momento angular total (tanto orbital como de espín) permanece invariable en toda interacción.
Y la lista podría continuar.