Ley de Conservación de la Cantidad de Movimiento

La ley de conservación de la cantidad de movimiento establece que, en un sistema aislado (es decir, sin fuerzas externas), la cantidad total de movimiento $ \vec{P} $ permanece constante: $$ \vec{P} = \sum_i m_i \vec{v}_i $$ donde $m$ es la masa de cada partícula y $\vec{v}$ su velocidad.

La cantidad de movimiento resulta de combinar masa y velocidad:

$$ \vec{p} = m \vec{v} $$

Esta magnitud refleja la capacidad de un cuerpo en movimiento para influir en otros cuando interactúa con ellos, ya que depende tanto de su masa como de su rapidez.

Por ejemplo, un camión tiene una masa muy grande y, aunque se desplace despacio, posee una cantidad de movimiento considerable. Una pelota de ping-pong, en cambio, es tan ligera que, incluso a gran velocidad, su cantidad de movimiento resulta prácticamente despreciable.

Según la ley de conservación de la cantidad de movimiento, si no actúa ninguna fuerza externa sobre un sistema, la cantidad total de movimiento antes y después de cualquier interacción permanece invariable:

$$ \vec{P}_{\text{inicial}} = \vec{P}_{\text{final}} $$

La cantidad de movimiento es, por tanto, una magnitud conservada, aunque solo en sistemas cerrados y aislados.

Un ejemplo sencillo

Imagina a dos patinadores sobre un hielo perfectamente liso.

Al principio permanecen en reposo, por lo que la cantidad total de movimiento es cero. Cuando se impulsan mutuamente, uno se desliza hacia la derecha y el otro hacia la izquierda.

La cantidad de movimiento de un patinador es igual y opuesta a la del otro, de modo que el total sigue siendo cero, igual que al inicio.

En otras palabras, si la fuerza externa neta es nula ($\vec{F}_{\text{ext}}=0$), entonces:

$$ \frac{d\vec{P}}{dt} = 0 \quad \Rightarrow \quad \vec{P}_{\text{inicial}} = \vec{P}_{\text{final}} $$

Ejemplo 2

Consideremos dos bolas de billar, cada una con una masa de 200 gramos, que se mueven con distintas velocidades iniciales:

• Bola A: $m_A = 0.2 \,\text{kg}$, velocidad inicial $v_A = 5 \,\text{m/s}$.
• Bola B: $m_B = 0.2 \,\text{kg}$, inicialmente en reposo ($v_B = 0$).

La bola A avanza a 5 m/s mientras la bola B permanece quieta.

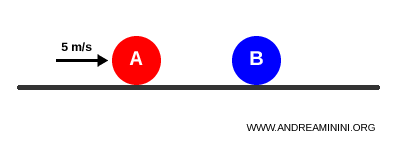
Antes de la colisión, la cantidad total de movimiento del sistema es de 1 kg·m/s:

$$ p_{\text{tot}} = m_A v_A + m_B v_B = 0.2 \cdot 5 + 0.2 \cdot 0 = 1.0 \,\text{kg·m/s} $$

Cuando la bola A impacta de frente con la bola B:

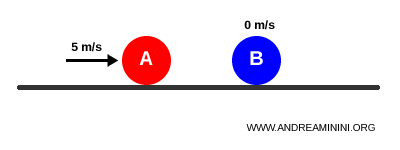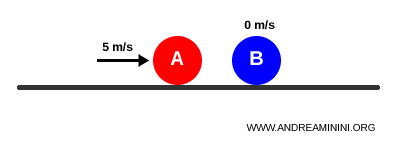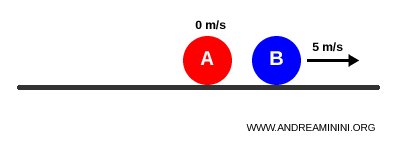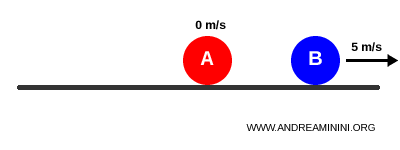
Tras una colisión elástica, la bola A se detiene mientras la bola B se mueve a 5 m/s:

$$ v_A' = 0 \qquad v_B' = 5 \,\text{m/s} $$

La cantidad total de movimiento permanece inalterada:

$$ p_{\text{tot, final}} = m_A v_A' + m_B v_B' = 0.2 \cdot 0 + 0.2 \cdot 5 = 1.0 $$

Así, tanto en colisiones elásticas como inelásticas, la cantidad total de movimiento del sistema se conserva.

Ejemplo 3

Pensemos ahora en un fusil de masa $m_f = 4 \,\text{kg}$ y una bala de masa $m_p = 0.02 \,\text{kg}$.

Al inicio, el fusil está en reposo, por lo que la cantidad total de movimiento es cero:

$$ p_{\text{inicial}} = 0 $$

Al disparar, la bala sale del cañón con una velocidad de $v_p = 400 \,\text{m/s}$.

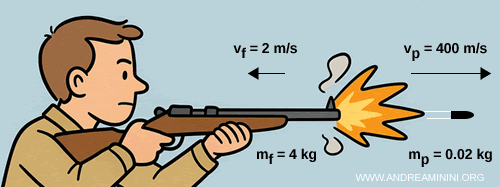
La cantidad de movimiento de la bala es:

$$ p_p = m_p \cdot v_p = 0.02 \cdot 400 = 8 \,\text{kg·m/s} $$

Por conservación de la cantidad de movimiento, el fusil adquiere una cantidad igual y opuesta:

$$ p_f = -8 \,\text{kg·m/s} $$

Esto equivale a una velocidad de retroceso de 2 m/s:

$$ v_f = \frac{p_f}{m_f} = \frac{-8}{4} = -2 \,\text{m/s} $$

De ahí procede el retroceso característico de las armas de fuego.

En conjunto, la cantidad total de movimiento se mantiene en cero:

$$ p_{\text{tot}} = p_p + p_f = 8 - 8 = 0 $$

La distribución, sin embargo, es muy desigual: la bala ligera adquiere una velocidad enorme, mientras que el fusil pesado se mueve lentamente en sentido contrario.

Fundamento teórico

La conservación de la cantidad de movimiento se deriva de un principio más profundo: la simetría espacial.

Decimos que el espacio es homogéneo cuando las leyes de la física son idénticas en cualquier punto.

En otras palabras, desplazar un sistema unos metros hacia un lado u otro no modifica las ecuaciones que describen su movimiento.

El teorema de Noether establece que toda simetría continua de un sistema físico corresponde a una magnitud conservada:

• Simetría temporal
  La invariancia frente a traslaciones en el tiempo implica la conservación de la energía.
• Simetría espacial
  La invariancia frente a traslaciones en el espacio implica la conservación de la cantidad de movimiento.
• Simetría rotacional
  La invariancia frente a rotaciones implica la conservación del momento angular.

Así, la invariancia traslacional garantiza la conservación de la cantidad de movimiento.

Y así sucesivamente.