Constante de acoplamiento
En física teórica, la constante de acoplamiento mide la intensidad de una interacción entre partículas.
Es el parámetro que determina con qué fuerza dos partículas se influyen mutuamente a través de una interacción fundamental.
En términos sencillos: cuanto mayor es la constante de acoplamiento, más fuerte es la interacción.
- Una constante pequeña indica una interacción débil (por ejemplo, en QED: $\alpha \approx 1/137$). En este régimen resultan viables los métodos perturbativos y las expansiones en series.
- Una constante grande señala una interacción intensa (por ejemplo, en QCD a bajas energías: $\alpha_s \sim 1$). En tales casos, los enfoques perturbativos dejan de ser aplicables.
¿Qué es la teoría de perturbaciones? La teoría de perturbaciones es una herramienta matemática que permite abordar problemas que, de otro modo, serían intratables. Si la interacción es débil, puede considerarse como una pequeña “perturbación” de un sistema más simple y no interactuante. Por ello, los métodos perturbativos solo resultan válidos cuando la constante de acoplamiento es reducida.
Estos son algunos ejemplos de constantes de acoplamiento asociadas a las cuatro fuerzas fundamentales de la naturaleza:
| Interacción | Constante | Símbolo | Valor típico |
|---|---|---|---|
| Electromagnética | Constante de estructura fina | α | ≈ 1/137 |
| Fuerte (QCD) | Acoplamiento fuerte | αs | Variable: ≈ 0.1 - 1 |
| Débil | Constante de Fermi ($G_F$) | - | ≈ 1.166 × 10-5 GeV-2 |
| Gravitatoria (en unidades naturales) | G | - | Extremadamente débil |
La función beta
En la teoría cuántica de campos, las constantes de acoplamiento no son verdaderamente constantes: dependen de la escala de energía.
La evolución de la constante de acoplamiento con la energía (y, por ende, con la distancia) está gobernada por la función beta.
Por ejemplo, en la QED (electrodinámica cuántica), el acoplamiento electromagnético $ \alpha $ varía con la energía de interacción $E$:
$$ \alpha(E) \ne \alpha(0) \quad \text{(la carga efectiva crece con la energía)} $$
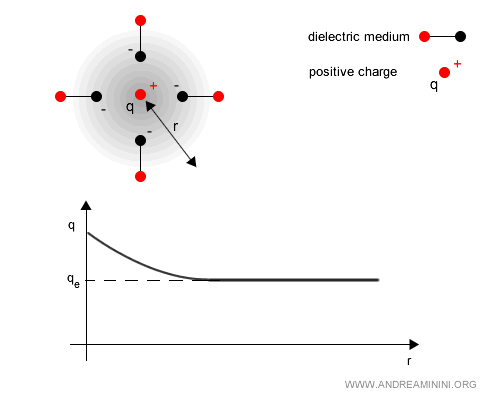
Este fenómeno se conoce como pantalla del vacío. A causa de las fluctuaciones cuánticas, el vacío actúa como un medio dieléctrico que “oculta” parte de la carga a bajas energías (es decir, a grandes distancias).
A energías más altas (o distancias más cortas), la pantalla se vuelve menos eficaz y la carga efectiva aumenta.
Ejemplo. El vacío cuántico se comporta como un dieléctrico porque los pares electrón-positrón virtuales se polarizan en presencia de una carga. Cerca de una carga positiva $q$, los electrones virtuales (negativos) son atraídos mientras que los positrones (positivos) son repelidos. Esta redistribución del campo atenúa la carga observable a gran distancia. En consecuencia, la carga efectiva $q_e(r)$ medida lejos resulta menor que la carga desnuda $q$.
En cambio, en la QCD (cromodinámica cuántica), el acoplamiento fuerte $\alpha_s$ disminuye al aumentar la energía o el cuadrado de la transferencia de momento $Q^2$:
$$ \alpha_s(Q^2) \downarrow \;\; \text{cuando} \;\; Q^2 \uparrow \quad \text{(libertad asintótica)} $$
Este efecto, denominado antipantalla, surge de las auto-interacciones de los gluones, ya que -a diferencia de los fotones- ellos mismos portan carga de color.
El resultado es que, a distancias extremadamente cortas (altas energías), la interacción entre quarks se debilita y estos se comportan casi como partículas libres dentro de un hadrón (por ejemplo, un protón o un neutrón). Este fenómeno recibe el nombre de libertad asintótica.
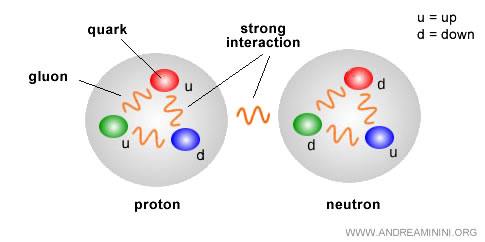
Ahora bien, cuando un quark intenta escapar de un hadrón, la interacción con el campo de color crece de manera abrupta, hasta volverse tan intensa que la separación resulta imposible. Este fenómeno es el confinamiento de quarks.
Nota. Este marco conceptual es esencial para comprender fenómenos como la libertad asintótica, la pantalla del vacío y, en general, la estructura de las interacciones fundamentales. Explica, por ejemplo, por qué en colisionadores de alta energía como el LHC los quarks parecen interactuar débilmente, aunque a escalas mayores el confinamiento los mantenga firmemente ligados dentro de los hadrones.
Notas adicionales
Algunas consideraciones complementarias:
- En una teoría gauge (como QED o QCD), la constante de acoplamiento $g$ aparece explícitamente en el lagrangiano: $$ \mathcal{L}_{\text{int}} = g \, \bar{\psi} \gamma^\mu A_\mu \psi $$ donde $g$ es la constante de acoplamiento, $A_\mu$ el campo gauge (fotón, gluón) y $\psi$ el campo de materia (electrón, quark).
Y así sucesivamente.