Partículas Sigma
Las partículas Sigma, representadas por la letra griega $ \Sigma $, son bariones formados por tres quarks y pertenecen a la familia de partículas que interactúan mediante la interacción fuerte. Su rasgo distintivo es la presencia de un quark extraño (s), responsable del número cuántico conocido como extrañeza.
Las partículas Σ están constituidas por tres quarks:
- $ \Sigma^+ = uus $
- $ \Sigma^0 = uds $
- $ \Sigma^- = dds $
En todos los casos, uno de los quarks es un quark extraño (s), mientras que los otros dos corresponden a combinaciones de quarks up (u) y down (d).
Carga eléctrica
La carga eléctrica de cada partícula se obtiene sumando las cargas eléctricas de los quarks que la componen. Los valores son:
- $ q(u) = +2/3 $
- $ q(d) = -1/3 $
- $ q(s) = -1/3 $
De este modo, las cargas eléctricas de las partículas Sigma resultan:
- $ q ( \Sigma^+ ) = +1 $
- $ q ( \Sigma^0 ) = 0 $
- $ q ( \Sigma^- ) = -1 $
Por ejemplo, la partícula $ \Sigma^+ $ está formada por dos quarks up y un quark extraño (uus). Su carga eléctrica se obtiene sumando las cargas individuales: $$ q ( \Sigma^+ ) = q(u) + q(u) + q(s) = \frac{2}{3} + \frac{2}{3} - \frac{1}{3} = \frac{3}{3} = +1 $$ La partícula $ \Sigma^0 $ está compuesta por un quark up, un quark down y un quark extraño (uds). Su carga eléctrica es: $$ q ( \Sigma^0 ) = q(u) + q(d) + q(s) = \frac{2}{3} - \frac{1}{3} - \frac{1}{3} = 0 $$ La partícula $ \Sigma^- $ está formada por dos quarks down y un quark extraño (dds). Su carga eléctrica resulta: $$ q ( \Sigma^- ) = q(d) + q(d) + q(s) = -\frac{1}{3} - \frac{1}{3} - \frac{1}{3} = -1 $$
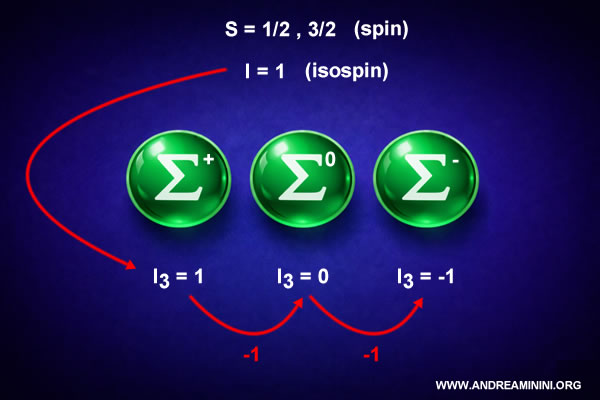
Isospín de las partículas Sigma
Las partículas Sigma poseen un isospín total igual a 1.
Esto se debe a que el isospín está asociado únicamente a los quarks up y down, mientras que el quark extraño no contribuye a este número cuántico.
Los quarks u y d se combinan formando un estado simétrico, lo que da lugar a un isospín total:
$$ I = 1 $$
Explicación. Los quarks $ u $ y $ d $ forman un doblete de isospín, mientras que el quark extraño queda excluido de esta estructura. Ambos quarks poseen isospín \( \tfrac12 \), con componentes terceras: $$ I_3(u) = +\frac{1}{2} $$ $$ I_3(d) = -\frac{1}{2} $$ La estructura del grupo SU(2) implica que, al combinar dos estados de isospín \( \tfrac12 \), solo pueden obtenerse dos valores posibles del isospín total, de acuerdo con las mismas reglas que rigen la suma de momentos angulares: \[ \frac{1}{2} \otimes \frac{1}{2} = 1 \oplus 0 \] Esto da lugar a un estado simétrico con \( I = 1 \) y a un estado antisimétrico con \( I = 0 \).
El estado simétrico con $ I = 1 $ forma un triplete asociado a las partículas Sigma: \[ \begin{aligned} |1,+1\rangle &= uu \\ |1,0\rangle &= \frac{1}{\sqrt2}(ud + du) \\ |1,-1\rangle &= dd \end{aligned} \] El estado antisimétrico con \( I = 0 \) corresponde a la partícula Lambda: \[ |0,0\rangle = \frac{1}{\sqrt2}(ud - du) \]
Es importante destacar que las partículas Sigma y Lambda poseen la misma composición en quarks (uds), pero difieren en su estructura de isospín.
¿Por qué se asigna I = 1 a las partículas Sigma (Σ) y I = 0 a la Lambda (Λ)?
Experimentalmente, las partículas Sigma se observan en tres estados de carga distintos ($ Σ^+, Σ^0, Σ^- $). Dado que el número de estados de un multiplete de isospín viene dado por $ 2I + 1 $, se obtiene:
$$ 2I + 1 = 3 \Rightarrow I = 1 $$
Por lo tanto, las Sigma forman un triplete. Esto implica que la parte de isospín de su función de onda es simétrica, es decir, permanece invariante bajo el intercambio de los quarks u y d:
$$ uu $$ $$ dd $$ $$ \frac{1}{\sqrt{2}}(ud + du) $$
En cambio, la partícula Lambda presenta un único estado observable ($ Λ^0 $), lo que implica:
$$ 2I + 1 = 1 \Rightarrow I = 0 $$
Por ello, la Lambda es un singlete. En este caso, la función de onda de isospín es antisimétrica, lo que significa que cambia de signo al intercambiar los quarks u y d:
$$ \frac{1}{\sqrt{2}}(ud - du) $$
En resumen, la diferencia entre las partículas Sigma y Lambda no reside en su contenido en quarks, sino en la forma en que estos se organizan en el espacio de isospín.
Si el isospín total es \( I = 1 \), el número de estados posibles es:
\[ 2I + 1 = 2 \cdot 1 + 1 = 3 \]
Esto significa que el multiplete de isospín contiene tres estados distintos, caracterizados por los valores de la tercera componente \( I_3 \):
$$ I_3 = \{ +1,\ 0,\ -1 \} $$
En el caso de las partículas Sigma, estos estados corresponden a:
- $ \Sigma^+ $
- $ \Sigma^0 $
- $ \Sigma^- $
Espín de las partículas Sigma
Existen dos familias distintas de partículas Sigma, que se diferencian por el valor de su espín total.
- Sigma (Σ)
Las partículas Sigma ordinarias tienen espín \( \frac{1}{2} \) y pertenecen al octete bariónico. En este caso, los espines de los quarks no están todos alineados (por ejemplo, una configuración posible es ↑↑↓), lo que da lugar a un espín total de 1/2: $$ \tfrac 12 + \tfrac 12 - \tfrac 12 = \tfrac 12 $$ - Sigma estrella (Σ*)
Las partículas Sigma* tienen espín \( \frac{3}{2} \) y pertenecen al decuplete bariónico. En este caso, los tres espines de los quarks están alineados (↑↑↑), dando lugar a un espín total de 3/2: $$ \tfrac 12 + \tfrac 12 + \tfrac 12 = \tfrac 32 $$ Estos estados corresponden a bariones excitados, con los espines completamente alineados.
La diferencia entre ambas familias se debe a la alineación relativa de los espines de los quarks.
Esto explica por qué partículas con el mismo contenido en quarks pueden presentar masas distintas y valores de espín diferentes.
Y así sucesivamente.