Coeficiente Beta
El coeficiente beta (o función beta) describe cómo varía la constante de acoplamiento de una interacción fundamental al cambiar la escala de energía: $$ \beta(g) = \mu \frac{d g}{d\mu} $$ Donde:
- $g$ es la constante de acoplamiento (por ejemplo, $\alpha$ en QED, $\alpha_s$ en QCD)
- $\mu$ es la escala de energía (o punto de renormalización)
- $\beta(g)$ indica cómo evoluciona $g$ con $\mu$ y en qué sentido.
En términos sencillos, el coeficiente beta nos muestra cómo cambia una fuerza fundamental (como la electromagnética o la fuerte) cuando exploramos distancias más cortas o energías más altas.
Es uno de los conceptos fundamentales de la teoría cuántica de campos.
La función beta se define como:
$$ \beta(g) = \mu \frac{d g}{d\mu} $$
Su interpretación física es directa:
- Si $\beta(g) > 0$, la interacción se intensifica al aumentar la energía (divergencia ultravioleta).
- Si $\beta(g) < 0$, la interacción se debilita con la energía (libertad asintótica).
En resumen, el coeficiente beta describe la evolución de una fuerza con la energía.
Ejemplo. En QED, el coeficiente beta es positivo, ya que la interacción electromagnética crece con la energía (apantallamiento). En QCD, en cambio, el coeficiente beta es negativo: la interacción fuerte se debilita a altas energías (antiapantallamiento). Esta diferencia es la base de ideas centrales de la física moderna como el confinamiento, la libertad asintótica y la evolución de las constantes fundamentales de la naturaleza.
Ejemplo
En Electrodinámica Cuántica (QED), el coeficiente beta es positivo:
$$ \beta(\alpha) > 0 $$
Esto significa que la carga efectiva aumenta con la energía, dando lugar al llamado apantallamiento del vacío.
A distancias muy cortas (altas energías), el fotón percibe menos polarización y la carga parece mayor.
A distancias largas, los efectos de polarización se acumulan y la carga efectiva disminuye.
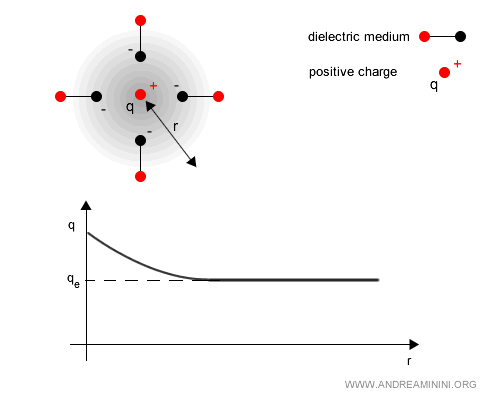
Ejemplo. El vacío cuántico se comporta como un medio dieléctrico: las fluctuaciones generan pares virtuales electrón-positrón que se polarizan en presencia de una carga $ q $. Para una carga positiva, los componentes negativos de los pares son atraídos, mientras que los positivos son repelidos. Esta polarización reduce la intensidad del campo eléctrico a grandes distancias, de modo que la carga efectiva $q_e(r)$ resulta menor que la carga desnuda $q$. En otras palabras, la carga real queda “apantallada.”
Ejemplo 2
En Cromodinámica Cuántica (QCD), el coeficiente beta es negativo:
$$ \beta(g_s) < 0 $$
Esto implica que la constante de acoplamiento disminuye con la energía, originando el antiapantallamiento.
A distancias muy cortas (altas energías), los quarks se comportan casi como partículas libres (libertad asintótica).
Por el contrario, al separarse, el acoplamiento crece y los quarks permanecen confinados dentro de los hadrones (como protones o neutrones). Este fenómeno recibe el nombre de confinamiento de quarks.
La función Beta en QCD
A un bucle, la función beta de la QCD es:
$$ \beta(g_s) = - \left( \frac{11}{3} N_c - \frac{2}{3} n_f \right) \frac{g_s^3}{16\pi^2} $$
Donde:
- $N_c = 3$ es el número de colores
- $n_f$ es el número de sabores de quarks
- $g_s$ es la constante de acoplamiento fuerte
El término $\frac{11}{3}N_c$ proviene de los gluones virtuales, que refuerzan la interacción a grandes distancias (antiapantallamiento).
El término $\frac{2}{3}n_f$ proviene de los bucles de quarks virtuales, que en cambio apantallan la interacción, como en la QED.
Mientras se cumpla $n_f < \frac{11}{2}N_c$, el coeficiente $ \beta(g_s) $ permanece negativo.
Nota. Con tres colores $ N_c = 3 $, la condición es: $$ n_f < \frac{11}{2} \cdot 3 = 16.5 $$ Por tanto, el comportamiento depende del número de sabores $ n_f $. Si hubiera demasiados, la contribución de los quarks dominaría, $ \beta > 0 $, y se perdería la libertad asintótica.
En la práctica, existen $ n_f=6 $ sabores, de modo que $n_f < 16.5$, y el coeficiente beta de la QCD es efectivamente negativo:
$$ \beta(g_s) < 0 $$
Esto significa que $g_s$ disminuye al aumentar la escala de energía.
En otras palabras, en la QCD la interacción fuerte se debilita a distancias muy cortas.
Este fenómeno es lo que denominamos libertad asintótica.
Nota. Esta es la razón por la que, en colisiones de ultraalta energía como las del CERN, los quarks se comportan casi como libres: su interacción se atenúa cuanto más profundamente exploramos (es decir, a energías más elevadas).
Una expresión simplificada
En la QCD, la función beta a un bucle puede escribirse de forma compacta (en unidades convenientemente normalizadas):
$$ \beta(g) \sim -\left(11n - 2f\right) $$
Donde $n = N_c$ (número de colores) y $f = n_f$ (número de sabores).
En muchas referencias aparece escrita así:
$$ \beta \propto -(11n - 2f) = 2f - 11n $$
o simplemente:
$$ \beta \sim (2f - 11n) $$
Los gluones aportan el término $11N_c$ (antiapantallamiento), mientras que los quarks (sabores) aportan el término $-2n_f$ (apantallamiento, como en la QED).
En QCD, la función beta es negativa siempre que $11n > 2f$, condición que garantiza la libertad asintótica.
Nota. Esta forma compacta resulta útil para analizar patrones generales, especialmente para valores arbitrarios de $N_c, n_f$ (por ejemplo, en modelos supersimétricos o teorías en dimensiones superiores), ya que pone de relieve la competencia entre las contribuciones de gluones y quarks a la función beta.
Y así sucesivamente.