Simetrías discretas en la física de partículas: C, P y T
En la física de partículas, las simetrías C, P y T son simetrías discretas que describen cómo se comportan las leyes fundamentales de la naturaleza cuando se aplican determinadas transformaciones idealizadas.
No se trata de transformaciones continuas, como rotaciones o traslaciones, sino de operaciones bien definidas que modifican de manera profunda el sistema físico que se analiza.
Las principales simetrías discretas que se estudian en la física de partículas son:
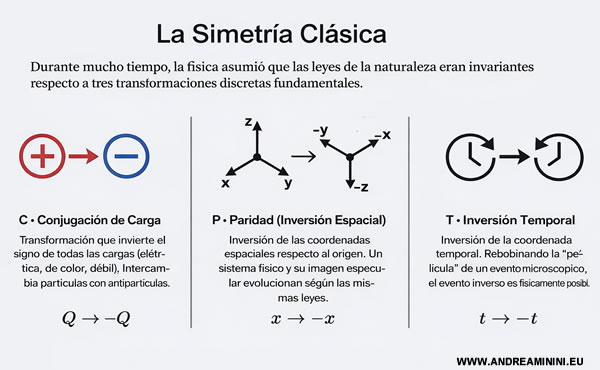
- Simetría C (conjugación de carga)
Sustituye cada partícula por su antipartícula correspondiente, invirtiendo el signo de todas las cargas. Permite estudiar cómo se comportan las leyes físicas cuando la materia se intercambia por antimateria. - Simetría P (paridad)
Corresponde a una inversión espacial de las coordenadas, similar a una reflexión en un espejo que intercambia izquierda y derecha. Sirve para comprobar si un proceso físico es invariante bajo una inversión espacial. - Simetría T (inversión temporal)
Consiste en invertir el sentido del tiempo y analizar un proceso como si se reprodujera hacia atrás. Permite investigar si las leyes de la física describen de la misma forma la evolución hacia el pasado y hacia el futuro.
Durante mucho tiempo se asumió que estas simetrías eran universalmente válidas. Esta idea encajaba con la concepción tradicional de la naturaleza como un sistema profundamente simétrico.
Sin embargo, a partir de la década de 1950, diversos experimentos demostraron que algunas de estas simetrías se violan, especialmente en el contexto de la interacción débil. Este descubrimiento transformó nuestra comprensión de las leyes fundamentales y sigue siendo un tema central de la física de partículas actual.
Las violaciones de C, P y CP muestran que la naturaleza no es perfectamente simétrica, mientras que la conservación de CPT se mantiene como uno de los principios más sólidos y mejor establecidos de la física teórica moderna.
En este marco, el estudio de las simetrías discretas desempeña un papel clave, tanto como base conceptual del Modelo Estándar como herramienta para explorar teorías que lo amplíen o lo superen.
Simetría C (conjugación de carga)
La simetría C, conocida como conjugación de carga, consiste en reemplazar cada partícula por su antipartícula correspondiente.
Es una transformación que actúa directamente sobre la identidad de las partículas elementales, invirtiendo todos los números cuánticos aditivos asociados a las cargas.
Por ejemplo, una partícula con carga negativa, como el electrón, se transforma en una partícula con la misma masa y el mismo espín, pero con carga opuesta, el positrón.
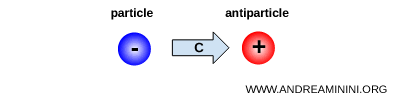
Desde el punto de vista físico, la transformación C invierte el signo de todas las cargas, no solo la carga eléctrica, sino también las asociadas a otras interacciones fundamentales, como la carga débil y la carga de color.
Por ejemplo, un quark up con carga eléctrica \( +\tfrac{2}{3} \) y un determinado color se transforma, bajo la acción de la simetría C, en un antiquark up con carga eléctrica \( -\tfrac{2}{3} \) y el anticolor correspondiente. De forma análoga, un neutrino se transforma en su antineutrino, con números cuánticos débiles de signo opuesto.
¿Qué interacciones fundamentales conservan la simetría C?
Las interacciones electromagnética, fuerte y gravitatoria conservan la simetría C.
Esto significa que, al sustituir todas las partículas por sus antipartículas correspondientes, las ecuaciones que describen estas interacciones mantienen la misma forma matemática.
La interacción débil, en cambio, viola la simetría C de manera máxima.

Un ejemplo especialmente claro lo proporcionan los neutrinos. Un neutrino zurdo, tras una transformación C, se convierte en un antineutrino zurdo. Sin embargo, en el Modelo Estándar, los antineutrinos zurdos no participan en las interacciones débiles. Esto muestra de forma directa que la simetría C no se conserva.

Esta violación también es relevante en cosmología, ya que, junto con la violación de CP, contribuye a explicar el exceso observado de materia frente a antimateria en el universo.
Simetría P (paridad)
La transformación de paridad (P) invierte el signo de las coordenadas espaciales. En tres dimensiones, esta operación equivale a una inversión central respecto del origen.
\[ (x,y,z) \rightarrow (-x,-y,-z) \]
En otras palabras, cada eje cartesiano se invierte con respecto a su orientación original.
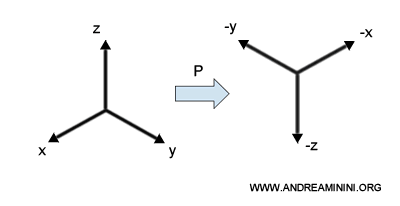
Desde el punto de vista físico, la paridad equivale a observar un fenómeno a través de un espejo ideal que invierte todas las direcciones espaciales.
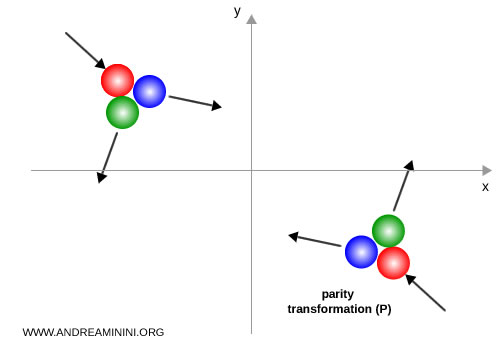
Si la simetría P se conserva, el proceso físico y su imagen especular están regidos por las mismas leyes y resultan indistinguibles desde el punto de vista físico.
Por ejemplo, si una bola de billar roja golpea a otras dos bolas, el proceso se desarrolla del mismo modo incluso después de invertir todas las coordenadas espaciales. En este caso, la dinámica de la colisión permanece invariante bajo la transformación de paridad, ya que las leyes de la mecánica clásica son simétricas frente a la inversión espacial.
La mayoría de las interacciones fundamentales conservan la simetría de paridad P, en particular las interacciones fuerte, electromagnética y gravitatoria.
Esto implica que, para estas interacciones, los procesos físicos ocurren de la misma forma aunque se intercambien izquierda y derecha.
No todas las interacciones cumplen esta propiedad. La interacción débil viola la simetría de paridad P. Esta violación indica que la naturaleza distingue de manera intrínseca entre configuraciones diestras y zurdas, introduciendo una asimetría fundamental en las leyes físicas.

En 1957, el experimento realizado por Chien Shiung Wu sobre el decaimiento beta del Cobalto 60 demostró de forma inequívoca que la interacción débil viola la simetría de paridad.
Los núcleos de Cobalto 60, enfriados y alineados mediante un campo magnético, emitían electrones de manera preferente en una dirección opuesta al espín nuclear, rompiendo así la simetría especular.
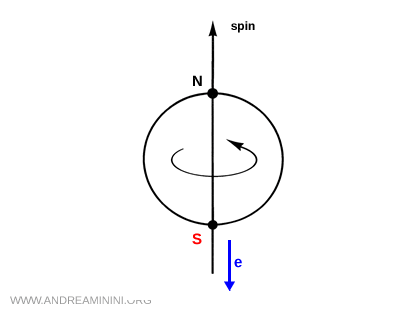
Dado que el espín es un pseudovector y no cambia de signo bajo una inversión espacial, tras aplicar la transformación de paridad P se esperaría que los electrones se emitieran en la misma dirección que el espín. Este comportamiento no se observa en la naturaleza, lo que constituye una evidencia experimental clara de la violación de la simetría de paridad.
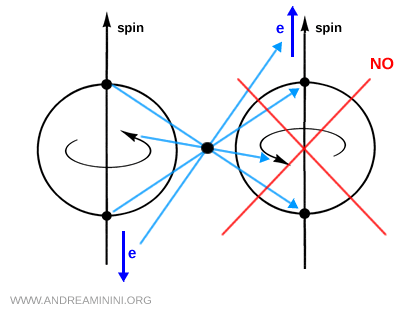
La conclusión es clara: a nivel fundamental, la naturaleza distingue entre izquierda y derecha.
La interacción débil es quiral: solo las componentes zurdas de las partículas y las componentes diestras de las antipartículas participan en las interacciones débiles cargadas.
Nota. En mecánica cuántica, los estados pueden clasificarse según su comportamiento bajo la transformación de paridad. Un estado se denomina par si su función de onda permanece invariante, e impar si cambia de signo. Esta clasificación es especialmente útil en el estudio de estados ligados y procesos de decaimiento.
Simetría T (inversión temporal)
La simetría T describe la invariancia de las leyes físicas cuando se invierte el sentido del tiempo. En términos intuitivos, una transformación T equivale a cambiar la orientación de la flecha del tiempo.
\[ t \rightarrow -t \]
Si una teoría es invariante bajo T, un proceso físico observado hacia atrás en el tiempo está gobernado por las mismas leyes dinámicas que describen su evolución hacia adelante.
Un ejemplo especialmente claro lo ofrecen las bolas de billar. Una bola roja golpea simultáneamente a otras dos bolas, una azul y una verde, que se separan en direcciones distintas. Si la escena se observa al revés en el tiempo, las dos bolas se aproximan a la bola roja, colisionan con ella y provocan su retroceso. Desde el punto de vista de las leyes del movimiento, el proceso es perfectamente admisible en ambas direcciones temporales y no aparece ninguna distinción fundamental entre pasado y futuro.
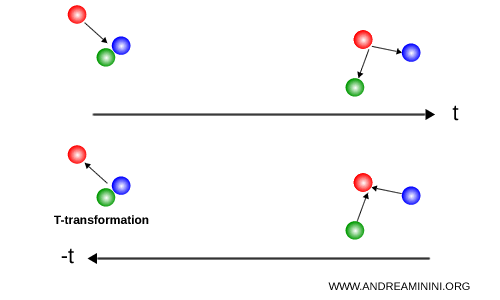
A escala macroscópica, esta simetría parece romperse debido a la segunda ley de la termodinámica, que introduce una dirección privilegiada del tiempo asociada al aumento continuo de la entropía.

Esta asimetría no se considera fundamental, sino un fenómeno emergente que surge de consideraciones estadísticas relacionadas con el comportamiento colectivo de sistemas con un número enorme de grados de libertad.
A nivel microscópico, en cambio, la mayoría de las leyes dinámicas fundamentales son invariantes bajo la inversión temporal.
Existe, sin embargo, una excepción de gran importancia. Dado que el teorema CPT debe cumplirse de forma exacta, la observación experimental de una violación de la simetría CP implica necesariamente la existencia de una correspondiente violación de la simetría T en las interacciones débiles. Aunque esta violación es fundamental, su observación directa resulta considerablemente más compleja.
Simetría CP
La simetría CP se define como la aplicación conjunta de la conjugación de carga (C) y la paridad (P).
Bajo una transformación CP, una partícula se reemplaza primero por su antipartícula mediante la operación C y, a continuación, se invierten las coordenadas espaciales del estado resultante mediante la operación de paridad P.
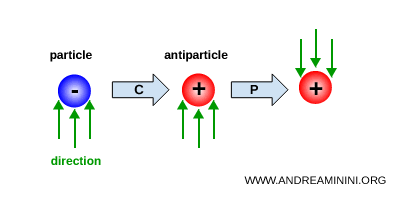
Tras el descubrimiento de la violación de la paridad, se pensó inicialmente que la simetría CP podría conservarse y representar una simetría más profunda de la naturaleza.
De hecho, cuando las transformaciones C y P se aplican simultáneamente al caso de los neutrinos, se obtiene un antineutrino diestro, en concordancia con las observaciones experimentales.
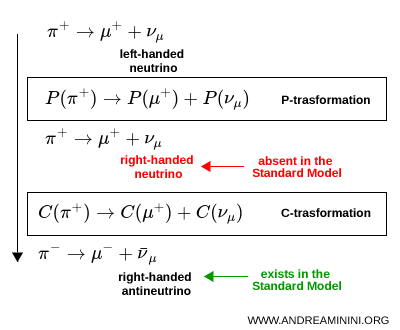
Esta expectativa fue desmentida en 1964, cuando el estudio de los decaimientos de kaones neutros demostró que la simetría CP también se viola en las interacciones débiles.
En particular, se observó que el comportamiento de los kaones y los antikaones presenta ligeras diferencias incluso después de aplicar la transformación CP.
Nota. Este descubrimiento tuvo un impacto profundo en la física teórica, ya que la violación de CP es una de las condiciones necesarias para explicar la asimetría observada entre materia y antimateria en el universo. En ausencia de dicha violación, materia y antimateria se habrían producido en cantidades iguales durante las primeras etapas de la evolución cósmica y se habrían aniquilado mutuamente.
Simetría CPT y teorema CPT
La simetría CPT combina las tres transformaciones discretas estudiadas anteriormente: conjugación de carga, paridad e inversión temporal.
El teorema CPT establece que toda teoría cuántica de campos que sea local, invariante bajo transformaciones de Lorentz y esté gobernada por un Hamiltoniano hermítico debe ser invariante bajo la transformación CPT combinada.
En otras palabras, si la carga, el espacio y el tiempo se invierten simultáneamente, las leyes de la física permanecen inalteradas. Incluso cuando C, P o CP se violan de manera individual, la transformación CPT debe seguir siendo una simetría exacta.
Por ejemplo, si $ \Psi $ representa un estado físico, entonces $ \Psi_{CPT} $ es también un estado físico y obedece las mismas leyes fundamentales.
$$ \Psi \ \text{(Estado físico)} \xrightarrow{C} C(\Psi) \xrightarrow{P} PC(\Psi) \xrightarrow{T} \Psi_{CPT} $$
Esto implica que un universo compuesto por antimateria, el llamado universo espejo, reflejado espacialmente y que evoluciona hacia atrás en el tiempo, obedecería exactamente las mismas leyes físicas que nuestro propio universo.

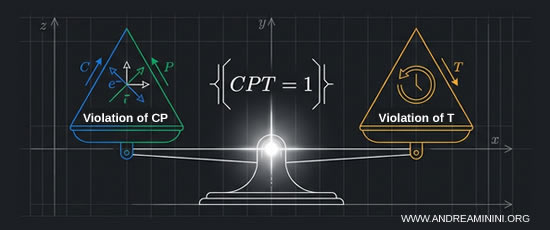
El teorema CPT implica además la existencia de una violación de la simetría T.
Para preservar la invariancia CPT, cualquier violación de la simetría CP debe ir acompañada de una violación correspondiente de la simetría T, es decir, de la invariancia bajo inversión temporal.
Las leyes microscópicas de la física no son, por tanto, perfectamente simétricas con respecto al tiempo.
Nota. Dado que se ha establecido experimentalmente que las simetrías C y P se violan, el teorema CPT implica necesariamente la existencia de una violación de la simetría T para que la transformación CPT combinada siga siendo una simetría exacta de las leyes fundamentales. Por consiguiente, si la simetría CP se viola, la simetría T también debe violarse. Conviene destacar que esta forma de irreversibilidad temporal es conceptualmente distinta de la flecha termodinámica del tiempo, cuyo origen es estadístico y macroscópico.
Hasta la fecha, la simetría CPT es la única combinación de estas transformaciones que se ha observado estrictamente conservada en todos los experimentos realizados. En la actualidad no existe evidencia experimental de su violación.
Cualquier posible violación de la simetría CPT implicaría una ruptura de la invariancia de Lorentz y exigiría una revisión profunda de nuestras teorías físicas fundamentales.
Y así sucesivamente.