Números leptónicos

Dado que existen tres familias de leptones, la física de partículas introduce tres números leptónicos diferentes:

• Número electrónico $L_e$
• Número muónico $L_\mu$
• Número tauónico $L_\tau$

En cada familia, los leptones tienen un valor de $+1$, mientras que sus antipartículas poseen $-1$.

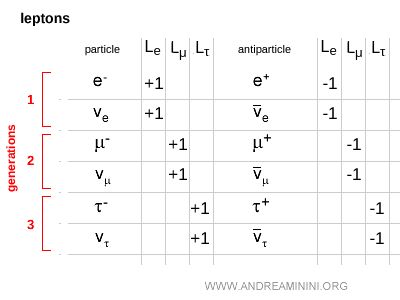
Por ejemplo, en la primera familia de leptones, el electrón $ e^- $ y el neutrino electrónico $ \nu_e $ tienen número leptónico electrónico $ L_e = +1 $, mientras que sus antipartículas - el positrón $ e^+ $ y el antineutrino electrónico $ \bar{\nu}_e $ - poseen $ L_e = -1 $. Todos los demás números leptónicos son nulos. 

Conservación del número leptónico

Los números leptónicos se conservan en todas las interacciones fundamentales.

En términos sencillos, esto significa que la suma total de los números leptónicos antes de una reacción debe coincidir con la suma después de ella.

Cualquier proceso que contradiga esta regla está prohibido en la naturaleza, al menos dentro del marco del Modelo Estándar.

• Interacción fuerte
  La fuerza fuerte no afecta a los leptones, por lo que los números leptónicos permanecen invariables. En una interacción puramente fuerte nunca se crean ni se destruyen leptones.
• Interacción electromagnética
  La fuerza electromagnética actúa sobre los leptones cargados (como el electrón), pero no modifica la familia a la que pertenecen. Por ello, los números leptónicos se mantienen constantes.
• Interacción débil
  La interacción débil puede transformar un leptón en otro dentro de la misma familia. Aun así, el número leptónico de cada familia se conserva de manera independiente. Cualquier proceso que lo violara simplemente no ocurre en la naturaleza.
  

  Nota. La interacción débil conserva por separado los números leptónicos de las tres familias. Por ejemplo, un electrón o un neutrino electrónico (primera generación) no puede transformarse en un muón o en un tau (segunda o tercera generación), y viceversa. Por eso hablamos de tres números leptónicos independientes ($ L_e,\quad L_\mu,\quad L_\tau $), cada uno de los cuales se mantiene en las interacciones débiles. Esta conservación estricta es característica de los leptones. Los quarks, en cambio, se comportan de otro modo: en sus interacciones débiles pueden mezclarse entre generaciones gracias a la matriz CKM (Cabibbo - Kobayashi - Maskawa), lo que significa que no existen “números cuárquicos” conservados de forma análoga a $L_e$, $L_\mu$ o $L_\tau$.

Ejemplo

El muón negativo $\mu^-$ pertenece a la segunda generación de leptones.

En el vacío, se desintegra espontáneamente por interacción débil en tres partículas: un electrón ($ e^- $), un antineutrino electrónico ( $ \bar{\nu}_e $ ) y un neutrino muónico ( $ \nu_\mu $ ).

$$ \mu^- \rightarrow e^- + \bar{\nu}_e + \nu_\mu $$

Para comprobar si esta desintegración es posible, analizamos los números leptónicos de todas las partículas implicadas:

$$ \underset{L_\mu = +1}{\mu^-} \;\;\rightarrow\;\; \underset{L_e = +1}{e^-} \;+\; \underset{L_e = -1}{\bar{\nu}_e} \;+\; \underset{L_\mu = +1}{\nu_\mu} $$

Verifiquemos la conservación en cada familia leptónica:

• Número electrónico ( $ L_e $ )
  Al inicio, el número electrónico total es cero: $$ L_e^{\text{inicial}} = 0 $$ Después de la desintegración: $$ L_e^{\text{final}} = +1 \ (\text{del } e^-) + (-1) \ (\text{del } \bar{\nu}_e) = 0 $$ Por lo tanto, el número electrónico se conserva. $$ L_e^{\text{inicial}} = L_e^{\text{final}} = 0 $$
• Número muónico ( $L_\mu$ )
  Al inicio: $$ L_\mu^{\text{inicial}} = +1 \ (\text{del } \mu^-) $$ Después de la desintegración: $$ L_\mu^{\text{final}} = +1 \ (\text{del } \nu_\mu) $$ Así, el número muónico se conserva. $$ L_\mu^{\text{inicial}} = L_\mu^{\text{final}} = +1 $$
• Número tauónico ( $L_\tau $ )
  No interviene ningún leptón tau, de modo que el número tauónico es cero tanto antes como después: $$ L_\tau^{\text{inicial}} = L_\tau^{\text{final}} = 0 $$

Esto demuestra que la desintegración del muón respeta la conservación independiente de los tres números leptónicos, razón por la cual se produce en la naturaleza.

Ejemplo 2

Consideremos ahora una desintegración distinta, meramente hipotética:

$$ \mu^- \rightarrow e^- + \gamma $$

Los números leptónicos distintos de cero en las partículas participantes son:

$$ \underset{L_\mu = +1}{\mu^-} \;\;\rightarrow\;\; \underset{L_e = +1}{e^-} + \gamma $$

En este caso, la conservación de los números leptónicos se viola tanto para $L_e$ como para $L_\mu$, ya que no aparecen neutrinos que compensen el cambio.

Por ello, esta desintegración no se da en la naturaleza o, si llegara a producirse, sería tan extraordinariamente rara que nunca se ha observado.

Comentarios finales

Algunas consideraciones adicionales sobre los números leptónicos:

• Oscilaciones de neutrinos y posibles violaciones
  El descubrimiento de las oscilaciones de los neutrinos demostró que, a grandes distancias, un neutrino puede transformarse en otro tipo de familia. Esto indica una ligera violación en la conservación de los números leptónicos individuales, aunque el número leptónico total permanece inalterado: $$L = L_e + L_\mu + L_\tau$$ Si este hecho se confirma plenamente, constituiría una pista de nueva física más allá del Modelo Estándar.

Y el debate sigue abierto…