Correspondencia biunívoca entre vectores y puntos en el plano

Todo punto $ P $ del plano, definido por sus coordenadas $ (x, y) $, puede asociarse de manera única con un vector $ \vec{v} = \begin{pmatrix} x \\ y \end{pmatrix} $. Este vector, denominado vector de posición, tiene su origen en el punto $ O $ y su extremo en $ P $. La correspondencia inversa también se verifica.
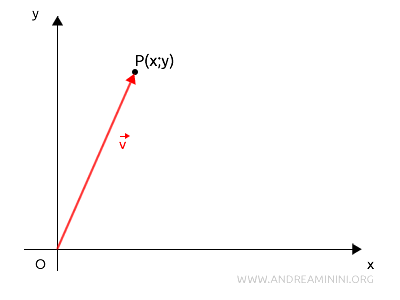
correspondencia entre vector y punto en el plano

En otras palabras, existe una correspondencia perfectamente biunívoca entre los puntos del plano $ P $ y los vectores del espacio vectorial $ \mathbb{R}^2 $.

Esto implica que los puntos del plano y los vectores en $ \mathbb{R}^2 $ representan dos perspectivas equivalentes de un mismo concepto: un punto puede representarse mediante un vector, y un vector define un punto único.

Dicha correspondencia depende de la elección de un origen $ O $, que actúa como referencia para definir los vectores de posición.

La correspondencia entre puntos del plano y vectores en $ \mathbb{R}^2 $ es biunívoca por las siguientes razones:

Cada punto del plano corresponde a un único vector de posición
Todo punto $ P(x, y) $ se representa de forma única mediante el vector $ \vec{OP} = \begin{pmatrix} x \\ y \end{pmatrix} $.
Cada vector corresponde a un único punto
Todo vector $ \begin{pmatrix} x \\ y \end{pmatrix} $ determina un único punto $ P(x, y) $ en el plano.

Ejemplo

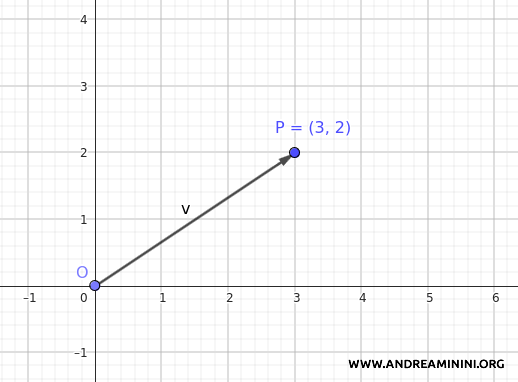
Por ejemplo, si un punto del plano tiene coordenadas $ P(3, 2) $, su vector de posición correspondiente es:

$$ \vec{OP} = \begin{pmatrix} 3 \\ 2 \end{pmatrix} $$

De forma recíproca, dado un vector $ \vec{v} = \begin{pmatrix} 3 \\ 2 \end{pmatrix} $, este se asocia al punto $ P(3, 2) $ en el plano.

ejemplo práctico de correspondencia entre vector y punto

Y así sucesivamente.