Vector equipolente
Dos vectores AB y CD se consideran equipolentes si tienen el mismo módulo, dirección y sentido.
La equipolencia es una relación de equivalencia.

Los vectores equipolentes no necesitan tener el mismo punto de origen. Pueden estar situados en posiciones diferentes dentro del plano o del espacio, siempre que conserven las mismas características geométricas.
Propiedades de los vectores equipolentes
Los vectores equipolentes cumplen las siguientes propiedades:
- Propiedad reflexiva. Todo vector es equipolente a sí mismo.
- Propiedad simétrica. Si el vector AB es equipolente al vector CD, entonces el vector CD es equipolente al vector AB.
- Propiedad transitiva. Si el vector AB es equipolente al vector CD y el vector CD es equipolente al vector EF, entonces el vector AB es equipolente al vector EF.
La clase de equivalencia
Los vectores equipolentes en el plano forman un conjunto denominado clase de equivalencia.
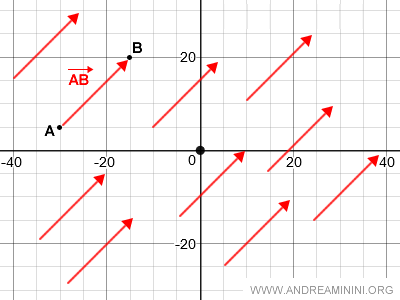
Cada clase de equivalencia recibe el nombre genérico de vector.
Dicha clase está formada por todos los vectores del plano que comparten el mismo módulo, dirección y sentido.