Representación vectorial de una recta

Un vector geométrico define una dirección que comparten todas las rectas del plano que son paralelas a dicho vector.

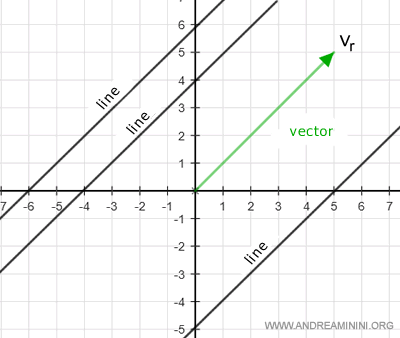
Por tanto, cualquier recta del plano puede describirse mediante:

• un vector geométrico no trivial v_r, denominado vector director, que determina la dirección de la recta: $$ v_r = \begin{pmatrix} l \\ m \end{pmatrix} $$

  Los parámetros l y m se conocen como los parámetros direccionales de la recta.

• un punto genérico P₀ del plano por el que pasa la recta: $$ P_0 = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} $$

  Ejemplo
  

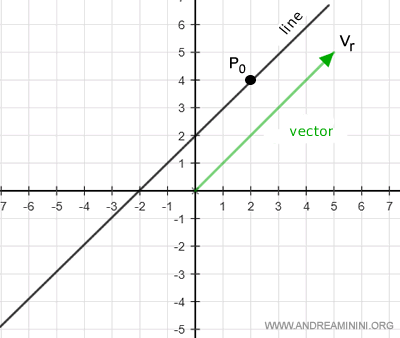
Un punto genérico del plano pertenece a la recta si existe un escalar α ∈ ℝ tal que:

$$ OP = OP_0 + \alpha v_r $$

Ejemplo

El punto P₁ tiene coordenadas (-5, -3).

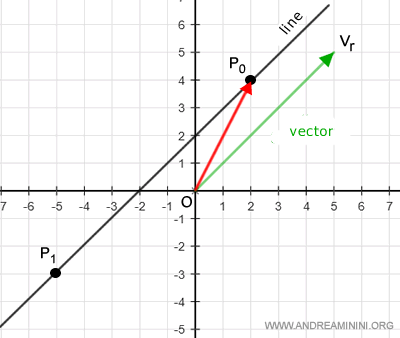
El punto P₁ pertenece a la recta si se verifica que:

$$ OP_1 = OP_0 + \alpha v_r $$

$$ \begin{pmatrix} -5 \\ -3 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} + \alpha \begin{pmatrix} 5 \\ 5 \end{pmatrix} $$

Resolvemos el sistema para determinar el valor de α:

$$ \begin{cases} -5 = 2 + 5 \alpha \\ -3 = 4 + 5 \alpha \end{cases} \Rightarrow \begin{cases} \alpha = - \frac{7}{5} \\ \alpha = - \frac{7}{5} \end{cases} $$

El sistema es compatible, y obtenemos α = -7/5.

Comprobación final:

$$ \begin{pmatrix} -5 \\ -3 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} + \alpha \begin{pmatrix} 5 \\ 5 \end{pmatrix} $$

$$ \begin{pmatrix} -5 \\ -3 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} + \begin{pmatrix} 5 \cdot ( - \frac{7}{5} ) \\ 5 \cdot ( - \frac{7}{5} ) \end{pmatrix} $$

$$ \begin{pmatrix} -5 \\ -3 \end{pmatrix} = \begin{pmatrix} 2 - 7 \\ 4 - 7 \end{pmatrix} $$

$$ \begin{pmatrix} -5 \\ -3 \end{pmatrix} = \begin{pmatrix} -5 \\ -3 \end{pmatrix} $$

Por tanto, el punto P₁ pertenece efectivamente a la recta.

Las coordenadas de todos los puntos que pertenecen a la recta se describen mediante la siguiente expresión, denominada ecuación vectorial de la recta: $$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} + \alpha \cdot \begin{pmatrix} l \\ m \end{pmatrix} $$ Si desarrollamos esta ecuación en un sistema de ecuaciones, obtenemos las ecuaciones paramétricas de la recta: $$ \begin{cases} x = x_0 + \alpha l \\ y = y_0 + \alpha m \end{cases} $$

Existen infinitas ecuaciones vectoriales y paramétricas, ya que el vector director puede multiplicarse por cualquier escalar no nulo.

Ecuaciones cartesianas

El vector P₀P₁ es paralelo al vector director v_r.

Según la teoría, un vector es paralelo y proporcional a otro si:

$$ \begin{pmatrix} x-x_0 & l \\ y - y_0 & m \end{pmatrix} \le 1 $$

Esto se verifica si:

$$ det \begin{pmatrix} x-x_0 & l \\ y - y_0 & m \end{pmatrix} = 0 $$

Calculando el determinante, obtenemos:

$$ m ( x-x_0 ) - l ( y - y_0 ) = 0 $$

Esta es la ecuación cartesiana de la recta.

Al igual que ocurre con las ecuaciones vectoriales y paramétricas, existen infinitas ecuaciones cartesianas equivalentes.