Rectas secantes

Se denominan rectas secantes a dos o más rectas distintas que se cruzan en un único punto.

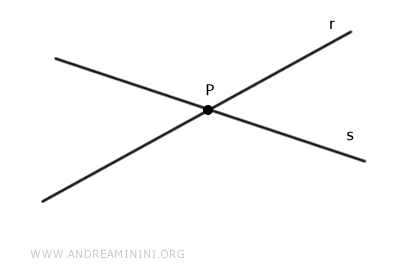
Dos rectas se intersectan cuando tienen exactamente un punto en común.

Esto se debe a que solo puede trazarse una recta que pase por dos puntos distintos.

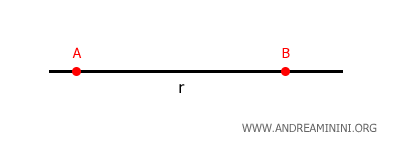
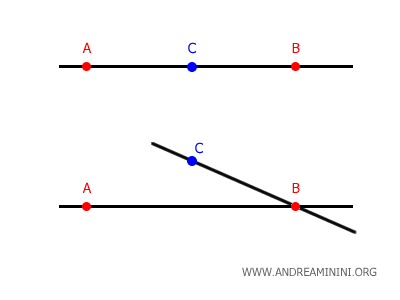
Si dos rectas comparten más de un punto, se las llama rectas coincidentes.

Por tanto, dos rectas solo pueden ser secantes si tienen un único punto en común.

La intersección de dos rectas divide el plano cartesiano en cuatro regiones, generando dos pares de ángulos opuestos por el vértice congruentes.

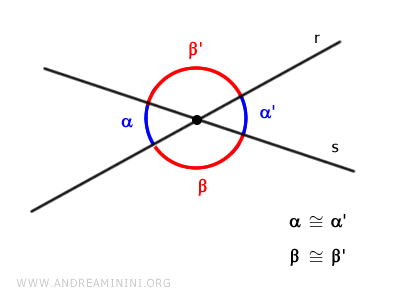
Según la medida de los ángulos que forman, las rectas secantes se clasifican en:

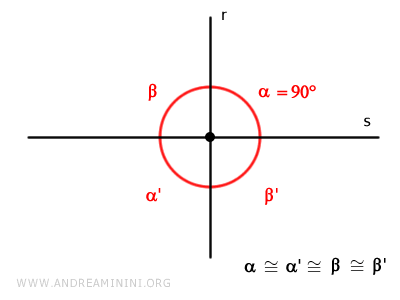
• Rectas perpendiculares
  Cuando los cuatro ángulos opuestos por el vértice miden 90°, las rectas son perpendiculares.
  
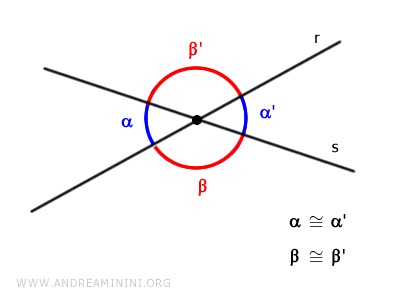
• Rectas oblicuas
  Cuando dos rectas secantes no son perpendiculares, se denominan rectas oblicuas.
  

Cómo hallar el punto de intersección de dos rectas en el plano

En geometría analítica, para encontrar el punto de intersección de dos rectas en el plano cartesiano, se resuelve un sistema de dos ecuaciones lineales. $$ \begin{cases} ax+by+c=0 \\ \\ a'x+b'y+c'=0 \end{cases} $$ Cada ecuación representa una recta en el plano.

Resolver este sistema puede arrojar tres posibles resultados:

• El sistema tiene solución única. En este caso, el sistema es compatible y la solución consiste en dos valores, x e y, que corresponden a las coordenadas (x;y) del punto de intersección. Esto significa que las rectas se cortan en un único punto. Sucede cuando los coeficientes «a» y «b» de las variables x e y no son proporcionales, lo que indica que las rectas tienen pendientes distintas. $$ \frac{a}{a'} \ne \frac{b}{b'} \Longleftrightarrow m \ne m' $$
• El sistema no tiene solución. En este caso, el sistema es incompatible. Significa que las rectas no se cortan y son paralelas entre sí. Esto ocurre cuando los coeficientes «a» y «b» de las variables x e y en ambas ecuaciones son proporcionales, pero el término independiente «c» no lo es. $$ \frac{a}{a'} = \frac{b}{b'} \ne \frac{c}{c'} $$
• El sistema tiene infinitas soluciones. En este caso, el sistema es indeterminado. Esto indica que las rectas son coincidentes y comparten todos sus puntos. Sucede cuando las razones entre los coeficientes y los términos independientes de ambas ecuaciones son proporcionales. $$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} $$

Mediante el álgebra es posible determinar el punto de intersección de dos rectas, si existe, y conocer la naturaleza de su relación: si son secantes, paralelas o coincidentes.

Ejemplo

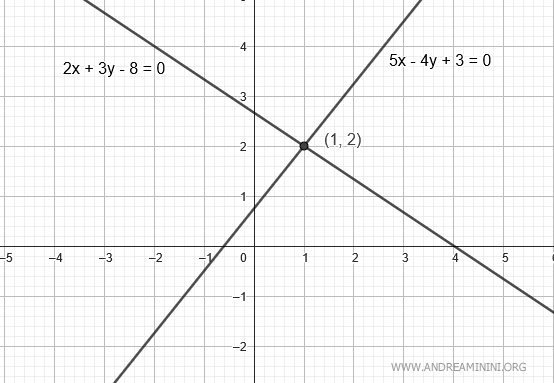
Consideremos dos rectas definidas por las siguientes ecuaciones implícitas:

$$ r: \ 2x+3y-8=0 $$

$$ r': \ 5x-4y+3=0 $$

Queremos determinar si se cortan, si son paralelas o si coinciden.

Para ello, calculamos la razón entre los coeficientes de las variables x e y.

$$ \frac{a}{a'} = \frac{2}{5} $$

$$ \frac{b}{b'} = \frac{3}{4} $$

Como las razones son distintas,

$$ \frac{a}{a'} \ne \frac{b}{b'} $$

las rectas se cortan.

Observaciones

Algunas consideraciones sobre las rectas secantes:

• Si dos rectas a y b se cortan, entonces sus respectivas paralelas a' y b' también se intersectan.
  

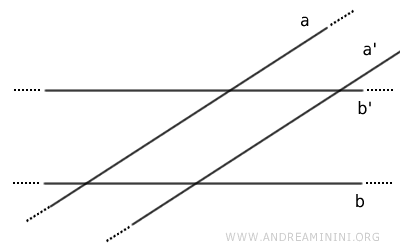
  Demostración. Por reducción al absurdo, supongamos lo contrario. Si dos rectas a y b son secantes, sus paralelas respectivas a' y b' serían paralelas entre sí a' // b' $$ a \parallel a' $$ $$ b \parallel b' $$ $$ a' \parallel b' $$ Sin embargo, si esto fuera cierto, por la propiedad transitiva, las rectas a y b también serían paralelas $$ a' \parallel b' \ , \ b' \parallel b \Rightarrow a \parallel b $$ Esto contradice el supuesto inicial de que a y b se cortan. Por tanto, la afirmación es falsa y su negación es verdadera: si dos rectas a y b se intersectan, sus respectivas paralelas a' y b' también se intersectan.

Y así sucesivamente