Distancia entre dos rectas

La distancia entre dos rectas se define como la distancia mínima entre puntos pertenecientes a ambas rectas. $$ d(r_1, r_2) := \min(P_{r1}, P_{r2}) $$

Para calcular la distancia entre dos rectas paralelas, se elige un punto P(x₀; y₀) sobre una de ellas y se mide la distancia desde ese punto a la otra recta $ ax+by+c=0 $:

$$ d = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}} $$

Otra posibilidad, si se conoce la pendiente m de ambas rectas paralelas $ y=mx+q_1 $ y $ y=mx+q_2 $, es emplear la siguiente fórmula:

$$ d = \frac{|q_2-q_1|}{\sqrt{1+m^2}} $$

Se distinguen los siguientes casos:

• Distancia cero. Si la distancia mínima es cero, las rectas son coincidentes (si son linealmente dependientes) o se intersectan (si son linealmente independientes).
• Distancia finita. Si la distancia mínima es un número positivo y finito, las rectas son paralelas.

Este esquema resume las distintas posibilidades.

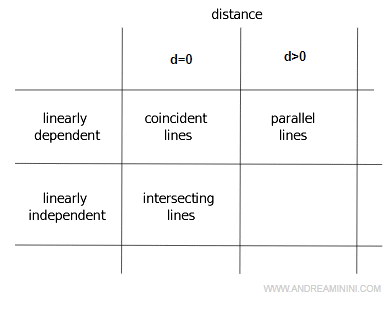
Cómo calcular la distancia entre rectas

En primer lugar, es necesario determinar si las rectas son paralelas, coincidentes o se cruzan, analizando la dependencia lineal de sus vectores directores.

1] Rectas linealmente dependientes

Si los vectores directores son linealmente dependientes, las rectas pueden ser coincidentes o paralelas.

¿Cómo saber si son coincidentes o paralelas?

Se toma un punto de una de las rectas y se calcula su distancia a la otra recta.

• Paralelas ( d > 0 ). Si la distancia es mayor que cero, las rectas son paralelas.
• Coincidentes ( d = 0 ). Si la distancia es cero, las rectas son coincidentes.

2] Rectas linealmente independientes

Si los vectores directores son linealmente independientes, las rectas necesariamente se intersectan.

Por tanto, existe un único punto común (punto de intersección) entre ambas rectas.

La distancia mínima es cero.

Ejemplos prácticos

Ejemplo 1

Tenemos las siguientes rectas:

$$ r_1: 5x+3y-6=0 $$

$$ r_2: -4x+4y-8=0 $$

Primero, comprobamos si son linealmente independientes.

Tomamos sus respectivos vectores normales:

$$ n_1 = \begin{pmatrix} 5 \\ 3 \end{pmatrix} $$

$$ n_2 = \begin{pmatrix} -4 \\ 4 \end{pmatrix} $$

Nota. La dependencia lineal puede comprobarse tanto con los vectores normales como con los vectores directores. Dado que son vectores perpendiculares entre sí, si los vectores normales son linealmente independientes, también lo son los vectores directores, y viceversa.

A continuación, calculamos el determinante de la matriz formada por estos vectores para verificar si son linealmente independientes:

$$ \det \begin{pmatrix} 5 & -4 \\ 3 & 4 \end{pmatrix} = 20 + 12 = 32 $$

El determinante es distinto de cero.

Esto indica que los dos vectores son linealmente independientes.

Por lo tanto, las dos rectas se intersectan, y la distancia mínima entre ellas es cero.

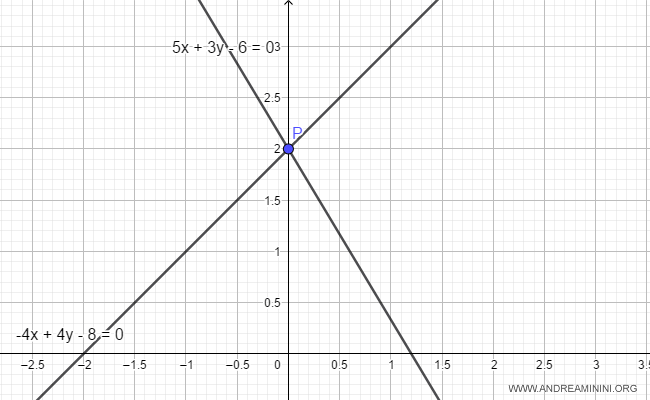
Nota. Para hallar el punto de intersección, se resuelve el sistema formado por ambas rectas: $$ \begin{cases} 5x+3y-6=0 \\ -4x+4y-8=0 \end{cases} $$ $$ \begin{cases} x=\frac{6-3y}{5} \\ -4\left(\frac{6-3y}{5}\right)+4y-8=0 \end{cases} $$ $$ \begin{cases} x=\frac{6-3y}{5} \\ y=2 \end{cases} $$ $$ \begin{cases} x=\frac{6-3(2)}{5} \\ y=2 \end{cases} $$ $$ \begin{cases} x=0 \\ y=2 \end{cases} $$

Ejemplo 2

Tenemos las siguientes rectas:

$$ r_1: 5x+3y-6=0 $$

$$ r_2: 15x+9y-3=0 $$

Primero, comprobamos si son linealmente independientes.

Tomamos sus respectivos vectores normales:

$$ n_1 = \begin{pmatrix} 5 \\ 3 \end{pmatrix} $$

$$ n_2 = \begin{pmatrix} 15 \\ 9 \end{pmatrix} $$

Luego, calculamos el determinante de la matriz formada por estos vectores para verificar si son linealmente independientes:

$$ \det \begin{pmatrix} 5 & 15 \\ 3 & 9 \end{pmatrix} = 45 - 45 = 0 $$

El determinante es cero.

Esto significa que los vectores son linealmente dependientes.

Por tanto, las dos rectas pueden ser paralelas o coincidentes.

¿Cómo determinar si son paralelas o coincidentes?

Tomamos cualquier punto sobre la recta r₁.

Por ejemplo:

$$ P = \begin{pmatrix} 0 \\ 2 \end{pmatrix} $$

Luego, calculamos la distancia entre el punto P y la otra recta r₂.

$$ D(P(x_0,y_0),r_2) = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}} $$

$$ D(P(0,2),r_2) = \frac{|15x+9y-3|}{\sqrt{15^2+9^2}} $$

$$ D(P(0,2),r_2) = \frac{|15(0)+9(2)-3|}{\sqrt{225+81}} $$

$$ D(P(0,2),r_2) = \frac{|15|}{\sqrt{306}} = 0.86 $$

La distancia entre el punto P y la recta r₂ es mayor que cero.

Por tanto, las dos rectas son paralelas.

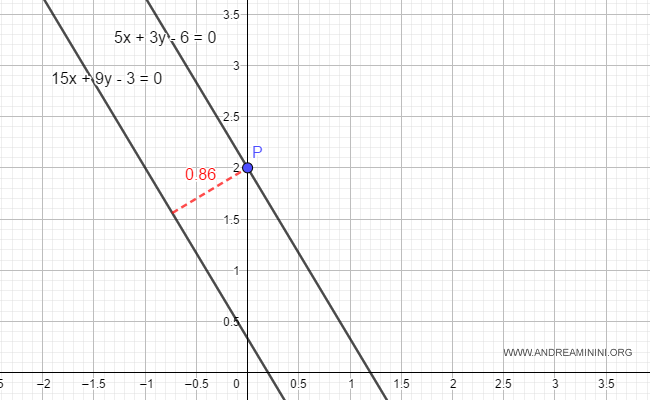
Nota. Si la distancia hubiera resultado ser cero, las rectas serían coincidentes.