Trapecio Isósceles

Un trapecio isósceles es un trapecio que posee dos lados no paralelos congruentes, es decir, de la misma longitud.

El trapecio isósceles forma parte de la familia de los trapecios, caracterizados por tener dos lados paralelos de longitud diferente, conocidos como base mayor (AB) y base menor (CD).

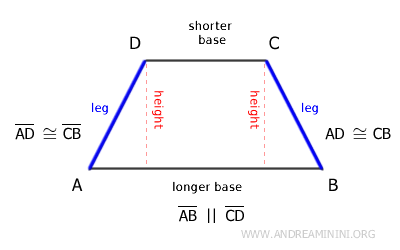
Su rasgo distintivo respecto a otros trapecios es que presenta dos lados no paralelos de igual longitud.

Un trapecio isósceles cuenta con las siguientes propiedades fundamentales:

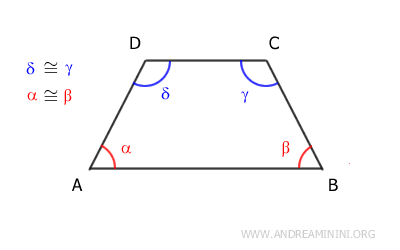
• Los ángulos adyacentes a la base mayor son congruentes (por ejemplo, α≅β).
• Los ángulos adyacentes a la base menor también son congruentes (por ejemplo, γ≅δ).
  
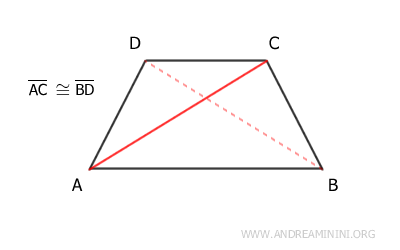
• Las diagonales son congruentes.
  

Fórmulas del Trapecio Isósceles

A continuación, algunas fórmulas clave relacionadas con el trapecio isósceles:

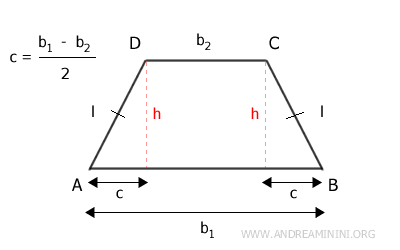
• Lado No Paralelo
  La longitud de cada lado no paralelo (l) puede calcularse mediante el teorema de Pitágoras. Se obtiene como la raíz cuadrada de la suma entre el cuadrado de la mitad de la diferencia de las bases, c = (b₁ - b₂)/2, y el cuadrado de la altura (h). $$ l = \sqrt{c^2 + h^2} $$
• Altura
  La altura (h) del trapecio isósceles puede deducirse a partir de la fórmula del lado no paralelo: $$ h = \sqrt{l^2 - c^2} $$ En esta expresión, l representa la longitud de un lado no paralelo, y c es la mitad de la diferencia entre las bases, es decir, c = (b₁ - b₂)/2.

Teorema del Trapecio Isósceles

En un trapecio isósceles, los ángulos adyacentes a cada base son congruentes.

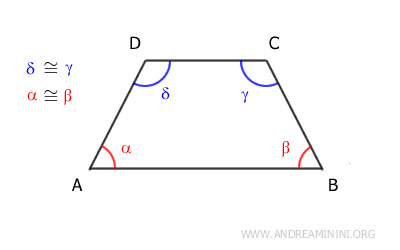
De esta propiedad se desprende que los ángulos opuestos en un trapecio isósceles son ángulos suplementarios, lo cual significa que su suma es igual a 180°.

$$ \alpha + \gamma = 180° $$

$$ \beta + \delta = 180° $$

También es válido el teorema recíproco:

Si en un trapecio los ángulos adyacentes a cada base son congruentes, entonces dicho trapecio es isósceles.

Y así sucesivamente...