Trapecio Rectángulo
Un trapecio rectángulo es un tipo de trapecio en el que uno de sus lados es perpendicular a las bases.
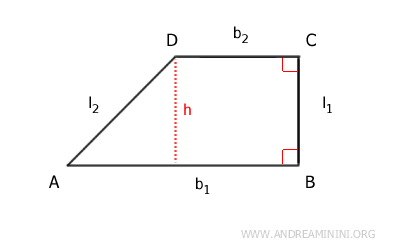
Se trata de una figura geométrica plana que forma parte de la familia de los cuadriláteros.
La característica distintiva de un trapecio rectángulo es que posee dos lados paralelos, denominados base mayor y base menor, y uno de los ángulos adyacentes a las bases mide exactamente 90 grados.
Ese ángulo recto es el que da nombre a esta figura.
Las Bases y la Altura
Un trapecio rectángulo tiene dos bases de longitudes distintas.
La base mayor (b1) es el lado paralelo de mayor longitud, mientras que la base menor (b2) es el lado paralelo más corto.
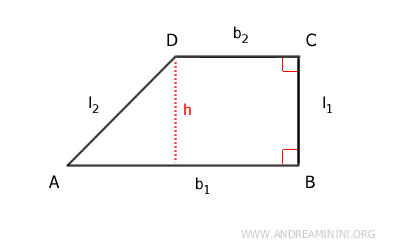
Los otros dos lados, l1 y l2, no son paralelos. Uno de ellos (l1) forma un ángulo recto con las bases.
La distancia perpendicular entre las dos bases se conoce como la altura del trapecio.
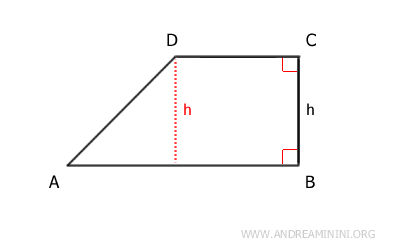
En un trapecio rectángulo, la altura coincide con el lado oblicuo que es perpendicular a las bases.
Fórmulas
Estas son las fórmulas fundamentales del trapecio rectángulo:
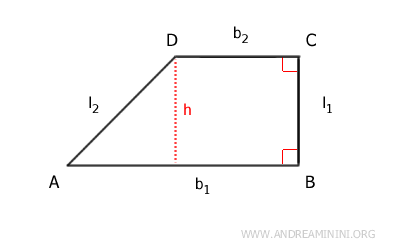
- Perímetro
El perímetro (P) de un trapecio rectángulo se obtiene sumando las longitudes de sus cuatro lados: $$ P = l_1 + l_2 + b_1 + b_2 $$ - Área
El área de un trapecio rectángulo se calcula, al igual que en cualquier trapecio, como la mitad del producto de la suma de las bases (b1 + b2) por la altura (h). $$ A = \frac{(b_1 + b_2) \cdot h}{2} $$ En esta fórmula, b1 representa la base menor, b2 la base mayor, y h es la altura del trapecio. - Lado Oblicuo
La longitud del lado oblicuo (l2) puede determinarse mediante el teorema de Pitágoras. Se calcula como la raíz cuadrada de la suma entre el cuadrado de la diferencia de las bases (b1 - b2) y el cuadrado de la altura (h). $$ l_2 = \sqrt{(b_1 - b_2)^2 + h^2} $$ - Altura
La altura (h) también puede deducirse aplicando el teorema de Pitágoras: $$ h = \sqrt{l_2^2 - (b_1 - b_2)^2} $$ donde l2 es el lado oblicuo del trapecio.
Y así sucesivamente...