Teorema del Segmento Medio en un Trapecio
En un trapecio, el segmento EF que une los puntos medios E y F de los lados no paralelos es paralelo a las bases y su longitud equivale a la media aritmética de las longitudes de ambas bases. $$ \overline{EF} = \frac{\overline{CD} + \overline{AB} }{2} $$
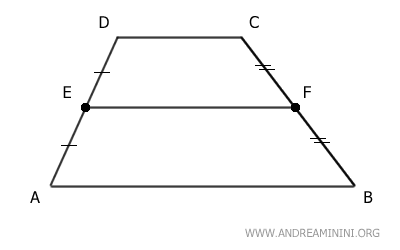
Un Ejemplo Práctico
Veamos el trapecio ABCD.
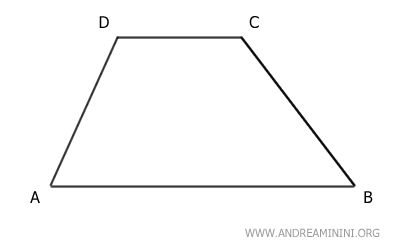
Los lados no paralelos AD y BC tienen sus puntos medios en E y F, respectivamente.
El segmento EF, que conecta estos puntos medios, es paralelo a las bases AB y CD del trapecio.
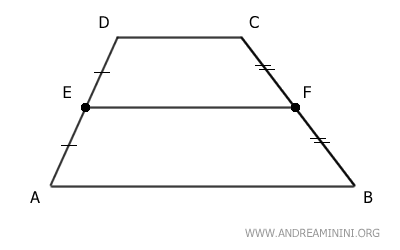
Además, la longitud del segmento EF corresponde a la mitad de la suma de las longitudes de las dos bases: (AB + CD)/2.
$$ \overline{EF} = \frac{\overline{CD} + \overline{AB} }{2} $$
Demostración
Analicemos ahora el trapecio ABCD.
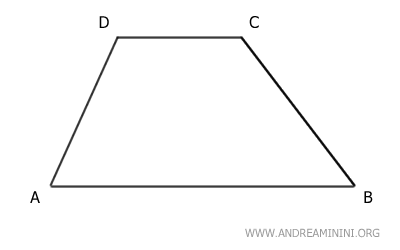
El punto E es el punto medio del lado no paralelo AD.
Esto significa que E divide el lado AD en dos segmentos congruentes, AE ≅ DE.
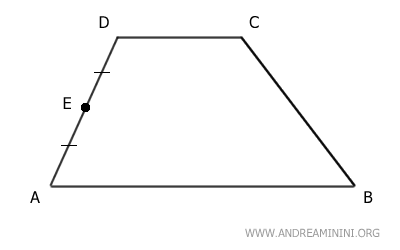
A continuación, se traza una recta r paralela a la base AB que pasa por el punto medio E del lado AD.
Según el Teorema de las Rectas Paralelas, esta recta corta al lado BC en su punto medio F, dividiendo BC en dos segmentos congruentes, BF ≅ CF.
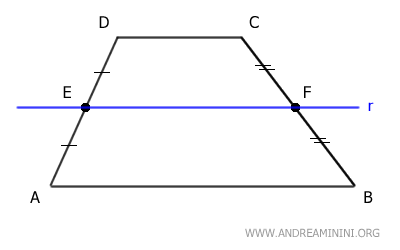
Consideremos ahora el segmento EF, que une los puntos medios de los lados no paralelos AD y BC.
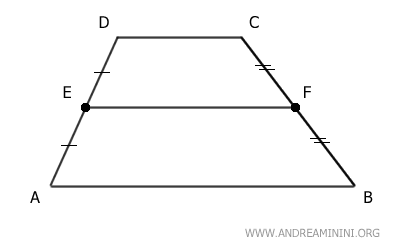
Se traza la diagonal AC, que divide el trapecio en dos triángulos y corta el segmento EF en el punto G.
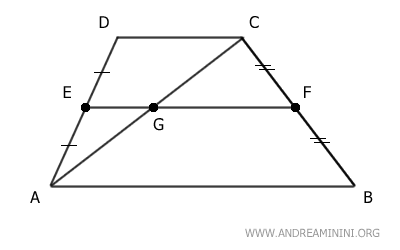
Analicemos el triángulo ACD.
El segmento EG, cuyo extremo está en el punto medio E del lado AD, es paralelo al lado CD del triángulo ACD.
Por lo tanto, según el Teorema del Segmento Medio de un Triángulo, el punto G es el punto medio del lado AC, y el segmento EG mide la mitad de la longitud del lado CD.
$$ \overline{EG} = \frac{ \overline{CD} }{2} $$
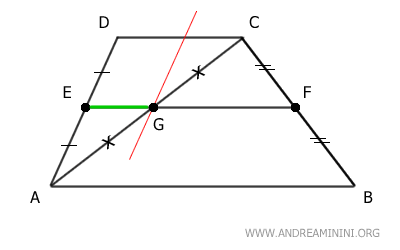
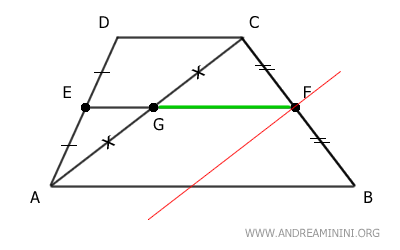
Analicemos ahora el triángulo ABC.
El segmento FG conecta el punto medio G del lado AC con el punto medio F del lado BC.
De acuerdo con el Teorema del Segmento Medio de un Triángulo, el segmento FG es paralelo y mide la mitad de la longitud del lado AB.
$$ \overline{FG} = \frac{ \overline{AB} }{2} $$
En síntesis, el segmento que une los puntos medios E y F de los lados no paralelos AD y BC del trapecio está compuesto por los segmentos EG y FG.
$$ \overline{EF} = \overline{EG} + \overline{FG} $$
Ambos segmentos, EG y FG, son paralelos a las bases AB y CD del trapecio.
Por tanto, el segmento EF es paralelo a las bases del trapecio.
Además, dado que EG = CD/2 y FG = AB/2, se concluye que la longitud del segmento EF es igual a la media aritmética de las longitudes de las bases del trapecio.
$$ \overline{EF} = \overline{EG} + \overline{FG} = \frac{ \overline{CD} }{2} + \frac{ \overline{AB} }{2} = \frac{\overline{CD} + \overline{AB} }{2} $$
Con esto, queda demostrada la validez del teorema del segmento medio en un trapecio.
Y así sucesivamente.