Segundo criterio de congruencia de triángulos
Dos triángulos son congruentes si tienen dos ángulos correspondientes congruentes y el lado comprendido entre dichos ángulos también congruente en ambos triángulos.
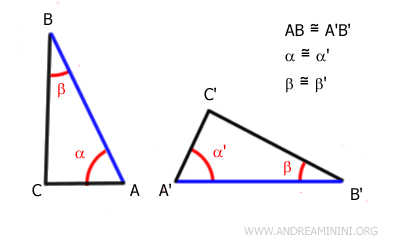
En otras palabras, dos triángulos son congruentes cuando poseen dos ángulos de igual medida y el lado comprendido entre ellos es de la misma longitud en ambos triángulos.
Este criterio es conocido como criterio Ángulo-Lado-Ángulo (ALA) o ASA (Angle-Side-Angle).
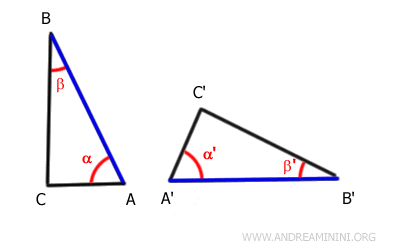
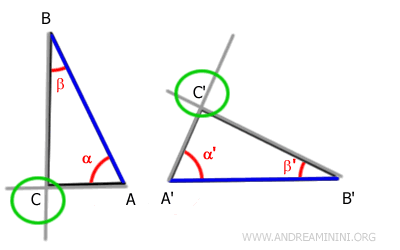
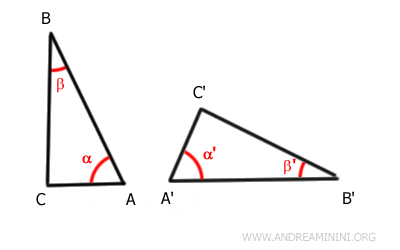
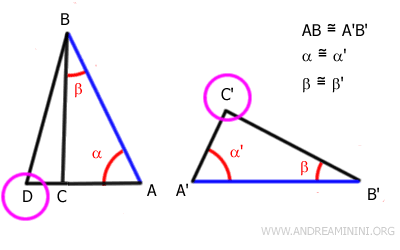
Por ejemplo, consideremos estos dos triángulos ABC y A'B'C'.
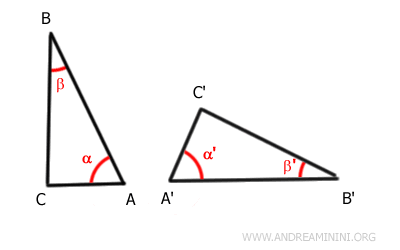
Los ángulos α≅α' y β≅β' son congruentes, es decir, tienen la misma medida.
Del mismo modo, los lados comprendidos entre estos ángulos, AB ≅ A'B', son congruentes, es decir, tienen la misma longitud.
De ello se deduce que los demás lados y ángulos de ambos triángulos también son congruentes.
Por lo tanto, los dos triángulos son congruentes; es decir, según la definición de congruencia, pueden superponerse punto por punto mediante un movimiento rígido.
Demostración
El segundo criterio de congruencia es un teorema, ya que puede demostrarse formalmente.
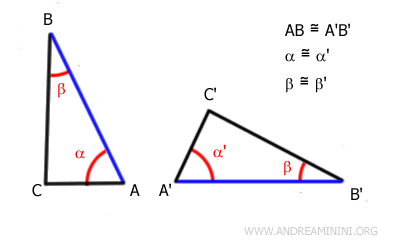
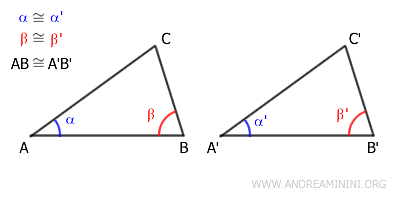
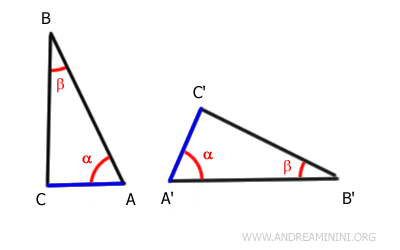
Supongamos los triángulos ABC y A'B'C'.
Por hipótesis, los ángulos α≅α' y β≅β' son congruentes, y el lado comprendido entre ellos AB ≅ A'B' es congruente.
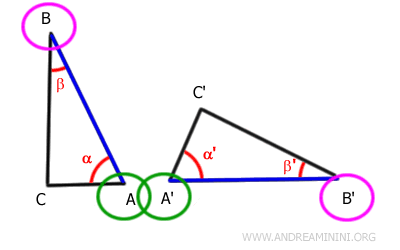
Si los lados AB y A'B' son congruentes, entonces pueden hacerse coincidir mediante un movimiento rígido.
Esto implica que los extremos de dichos lados se superponen: los puntos A con A' y los puntos B con B'.
Además, como los ángulos α≅α' son congruentes, los rayos que contienen los lados AC y A'C' también se superponen.
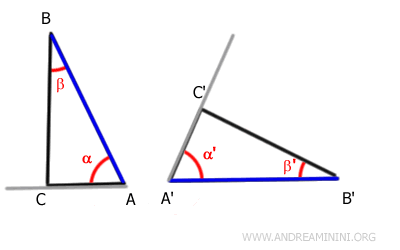
Del mismo modo, al ser congruentes los ángulos β≅β', los rayos que contienen los lados BC y B'C' también coinciden.
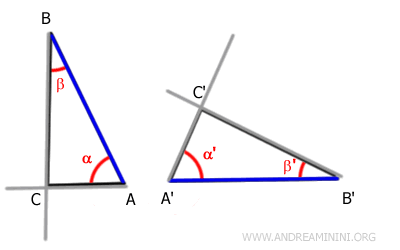
Como resultado, dichos rayos se cortan en un mismo punto.
Esto significa que los puntos C y C' coinciden.
En conclusión, todos los vértices de ambos triángulos coinciden en el mismo orden.
Esto implica que todos sus lados son congruentes: AB ≅ A'B', BC ≅ B'C', AC ≅ A'C'.
Y por lo tanto, todos los ángulos son congruentes.
De ello se sigue que los dos triángulos son congruentes.
Demostración alternativa
En este caso, emplearemos una demostración por contradicción.
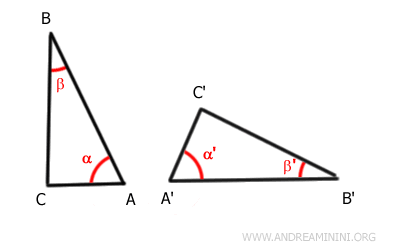
Supongamos que tenemos dos triángulos ABC y A'B'C', en los que dos ángulos son congruentes, \( \alpha \cong \alpha' \) y \( \beta \cong \beta' \), y un lado también es congruente, \( AB \cong A'B' \).
Supongamos ahora - en contra de lo que queremos demostrar - que los dos triángulos no son congruentes.
$$ ABC \not \cong A'B'C' $$
Si esto fuera cierto, entonces el lado AC tendría que ser mayor o menor que A'C'.
Supongamos que AC es mayor, es decir, $ AC > A'C' $. Entonces, podemos ubicar un punto P sobre AC tal que $ AP \cong A'C' $.
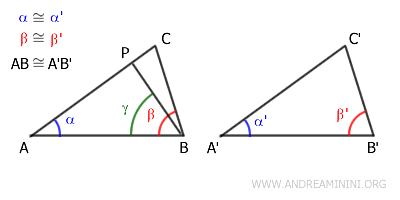
Consideremos ahora los triángulos ABP y A'B'C'. Cumplen las siguientes condiciones:
- Comparten un ángulo congruente por hipótesis: \( \alpha \cong \alpha' \).
- Comparten un lado congruente por hipótesis: \( AB \cong A'B' \).
- Por construcción, \( AP \cong A'C' \).
Según el primer teorema de congruencia, estos dos triángulos deben ser congruentes, es decir, todos sus lados y ángulos correspondientes son iguales.
$$ ABP \cong A'B'C' $$
En particular, esto implica que los ángulos correspondientes \( \gamma \) y \( \beta' \) son congruentes.

Sin embargo, por hipótesis tenemos que \( \beta \cong \beta' \), de modo que, por transitividad, también debería cumplirse \( \gamma \cong \beta \).
$$ \gamma \cong \beta' \cong \beta $$
Esto lleva a una contradicción: puesto que el punto \( P \) se encuentra en el interior del segmento \( AC \), el ángulo \( \gamma \) necesariamente debe ser menor que \( \beta \), lo cual contradice lo anterior.
Por tanto, nuestra suposición de que los triángulos no son congruentes es falsa.
En consecuencia, debe ser cierto que los dos triángulos son congruentes.
Nota: El mismo razonamiento se aplica si suponemos que \( AC < A'C' \), por lo que necesariamente \( AC \cong A'C' \).
Criterio generalizado de congruencia ALA de triángulos
El segundo criterio de congruencia de triángulos admite una versión extendida, conocida como "criterio generalizado de congruencia" o también como el "cuarto criterio de congruencia".
Dos triángulos son congruentes si poseen dos ángulos congruentes y un lado congruente en el mismo orden, aunque dicho lado no sea necesariamente el comprendido entre los dos ángulos.
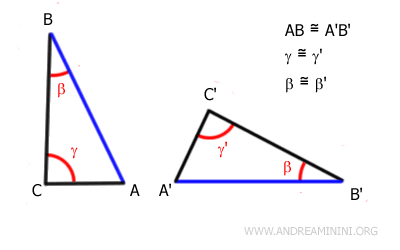
En este caso, el lado congruente puede ser cualquiera de los tres lados del triángulo; no es necesario que sea el lado comprendido entre los ángulos congruentes.
Dicho de otro modo: no es imprescindible que los ángulos congruentes sean adyacentes al lado congruente.
Sin embargo, es fundamental que los ángulos y el lado correspondan en el mismo orden relativo en ambos triángulos.
Ejemplo. Estos dos triángulos tienen ángulos correspondientes $ \alpha \cong \alpha' $ y $ \beta \cong \beta' $, y un lado congruente $ BC \cong B'C' $. Como los ángulos y el lado aparecen en el mismo orden relativo, podemos aplicar el criterio generalizado ALA y concluir que $ ABC \cong A'B'C' $.

Hasta aquí, todo correcto. Ahora tomemos el triángulo ABC y, con centro en A, tracemos un arco de radio AB que corte el segmento AC en el punto C'. A continuación, trazamos el segmento B'C' paralelo a BC. Así obtenemos un nuevo triángulo AB'C'. Por construcción, estos triángulos también presentan dos ángulos iguales $ \alpha $ y $ \beta \cong \beta' $, y un lado congruente $ AB \cong A'B' $. Sin embargo, los triángulos no son congruentes, $ ABC \not \cong AB'C' $, porque los ángulos y el lado no están dispuestos en el mismo orden relativo.
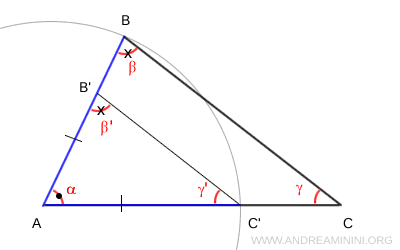
Este ejemplo demuestra claramente que, para aplicar el criterio generalizado ALA, los ángulos y el lado deben estar ordenados de manera correspondiente en ambos triángulos.
Demostración
Según el teorema de la suma de los ángulos interiores de un triángulo, la suma de los tres ángulos interiores es siempre 180°.
$$ \alpha + \beta + \gamma = 180° $$
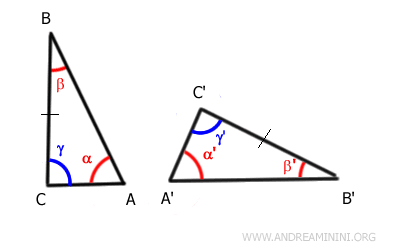
Por lo tanto, si dos ángulos de los triángulos ABC y A'B'C' son congruentes, $ \alpha \cong \alpha' $ y $ \beta \cong \beta' $, el tercer ángulo también será congruente por diferencia: $ \gamma \cong \gamma' $.
El ángulo restante $\gamma$ en ambos triángulos se calcula como:
$$ \gamma = 180° - \alpha - \beta $$
$$ \gamma' = 180° - \alpha' - \beta' $$
Como $ \alpha \cong \alpha' $ y $ \beta \cong \beta' $, se deduce que $ \gamma \cong \gamma' $.
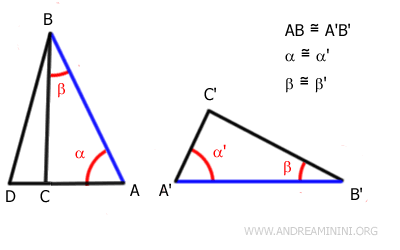
Supongamos ahora que los triángulos ABC y A'B'C' también tienen un lado congruente, por ejemplo $ BC \cong B'C' $, y que este lado se encuentra en la misma posición relativa en ambos triángulos.
En este caso, como $ \gamma \cong \gamma' $ y $ \beta \cong \beta' $, podemos concluir que los triángulos $ ABC \cong A'B'C' $ son congruentes por el criterio ALA, ya que presentan un lado y dos ángulos contiguos congruentes en el mismo orden.
Por tanto, dos triángulos son congruentes si tienen dos ángulos y un lado congruente, aunque dicho lado no sea necesariamente el comprendido entre los ángulos.
Demostración alternativa
El segundo criterio de congruencia puede demostrarse también por contradicción.
Consideremos dos triángulos ABC y A'B'C'.

Por hipótesis, los ángulos $ \alpha \cong \alpha' $ y $ \beta \cong \beta' $ son congruentes, y el lado comprendido entre ellos AB ≅ A'B' también es congruente.
Por tanto, según el segundo criterio de congruencia, los dos triángulos deberían ser congruentes.
Para llegar a una contradicción, supongamos que los lados AC y A'C' no son congruentes, es decir, que $ AC \ne A'C' $.
Según el postulado del transporte de segmentos, podemos localizar un punto D en el lado AC tal que $ AD = A'C' $.
Se traza el segmento BD y se considera el triángulo ABD.
Por el primer criterio de congruencia, los triángulos ABD y A'B'C' serían congruentes.
¿Por qué? Por construcción, $ AD \cong A'C' $; por hipótesis, $ AB \cong A'B' $, y el ángulo comprendido $ \alpha \cong \alpha' $. Por tanto, se cumple el primer criterio (Lado-Ángulo-Lado), y $ ABD \cong A'B'C' $.
En consecuencia, los ángulos en los vértices D y C' son congruentes.
Sin embargo, por hipótesis, los ángulos en C y C' ya eran congruentes, pues $ \gamma \cong \gamma' $.
Según el teorema de la suma de los ángulos interiores: $$ \alpha + \beta + \gamma = 180° $$ Si dos ángulos son congruentes, el tercero también lo es: $$ \gamma = 180° - \alpha - \beta $$ $$ \gamma' = 180° - \alpha' - \beta' $$ $$ \gamma \cong \gamma' $$
Por transitividad, el ángulo en D también sería congruente con el ángulo en C.
De ello se sigue que $ AD \cong AC $.
Pero como ya teníamos que $ AD \cong A'C' $, se deduce que $ AC \cong A'C' $.
$$ \overline{AC} \cong \overline{AD} \cong \overline{A'C'} $$
Esto contradice nuestra suposición inicial de que $ AC \ne A'C' $.
Por tanto, la suposición es falsa y necesariamente $ AC \cong A'C' $.
En conclusión, para establecer la congruencia de dos triángulos basta con que tengan dos ángulos y un lado congruente, aunque este no sea el lado comprendido entre los ángulos.
Y así sucesivamente.