Primer criterio de semejanza en triángulos
Dos triángulos se consideran semejantes cuando poseen dos ángulos correspondientes congruentes.
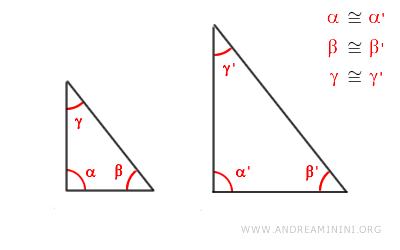
Cuando dos triángulos tienen dos pares de ángulos internos congruentes, se deduce necesariamente que el tercer ángulo en cada uno también es congruente.
Esto se basa en el principio fundamental de que la suma de los ángulos internos de cualquier triángulo siempre es igual a 180 grados.
$$ \alpha + \beta + \gamma \cong 180° $$
Por lo tanto, si dos pares de ángulos son congruentes, el tercer par también lo será de forma inevitable.
Así, los triángulos resultan semejantes porque mantienen idéntica proporción angular, mostrando la misma forma, aunque puedan diferir en tamaño.
$$ ABC \approx A'B'C' $$
Este criterio es conocido habitualmente como el criterio de semejanza AAA (Ángulo-Ángulo-Ángulo) para triángulos.
Un ejemplo ilustrativo
Consideremos los triángulos ABC y A'B'C'.
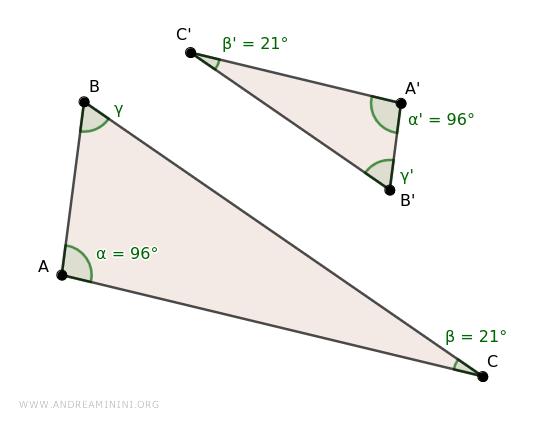
Los pares de ángulos α≅α' (96°) y β≅β' (21°) son congruentes.
Sabemos que la suma de los ángulos internos de un triángulo es siempre 180°:
$$ \alpha + \beta + \gamma = 180° $$
$$ \alpha ' + \beta ' + \gamma ' = 180° $$
Podemos deducir el valor de los ángulos γ y γ' a partir de los ángulos conocidos:
$$ \gamma = 180° - \alpha - \beta $$
$$ \gamma ' = 180° - \alpha ' - \beta ' $$
Dado que α≅α'≅96° y β≅β'≅21°, se obtiene:
$$ \gamma = 180° - 96° - 21° $$
$$ \gamma ' = 180° - 96° - 21° $$
Esto confirma que γ y γ' son congruentes, pues resultan de la misma operación algebraica sobre ángulos iguales.
$$ \gamma = 63° $$
$$ \gamma ' = 63° $$
Por tanto, los triángulos ABC y A'B'C' presentan ángulos congruentes α≅α' (96°), β≅β' (21°) y γ≅γ' (63°), lo que los hace semejantes.
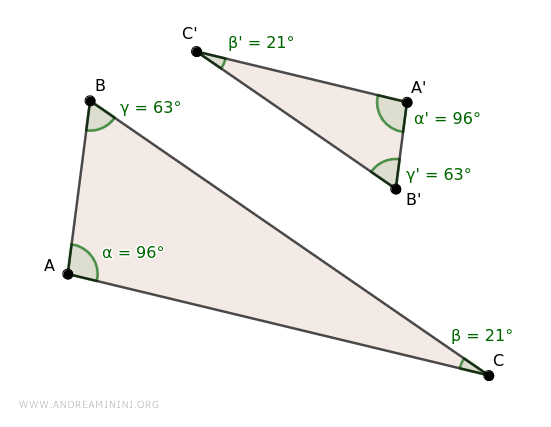
Demostración de la semejanza
Analicemos los triángulos ABC y A'B'C'.
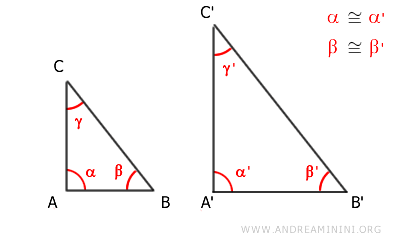
Partimos de la premisa de que los ángulos correspondientes α≅α' y β≅β' son congruentes:
$$ \alpha \cong \alpha ' $$
$$ \beta \cong \beta ' $$
Queremos demostrar que los triángulos ABC y A'B'C' son semejantes.
Para ello, debemos analizar si los segmentos comprendidos entre esos ángulos correspondientes, concretamente los lados AB y A'B', son congruentes o no.
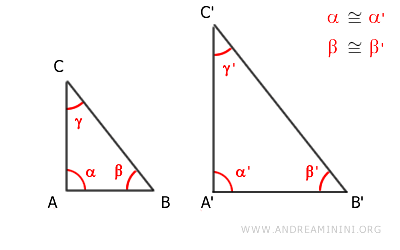
1) Congruencia de los lados AB y A'B'
Si los lados AB y A'B' son congruentes, entonces los triángulos ABC y A'B'C' son congruentes según el segundo criterio de congruencia de triángulos.
Por lo tanto, figuras congruentes son siempre semejantes, con razón de semejanza igual a 1, lo que confirma la semejanza en este caso.
2) No congruencia de los lados AB y A'B'
Si los lados AB y A'B' no son congruentes, se calcula la razón de semejanza \( k \) entre ellos:
$$ k = \frac{\overline{A'B'}}{\overline{AB}} $$
Luego se aplica una homotecia al triángulo ABC con centro en C y razón de semejanza \( k = \frac{A'B'}{AB} \).
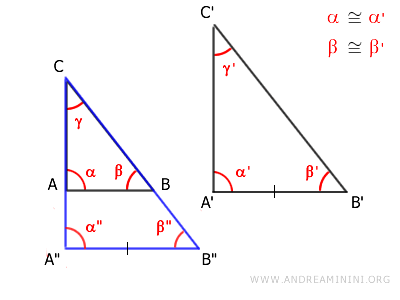
Por construcción, los segmentos A"B" y A'B' son congruentes, ya que ambos cumplen \( A'B' = k \cdot AB \) y \( A''B'' = k \cdot AB \).
$$ \overline{A''B''} \cong \overline{A'B'} $$
Además, la homotecia garantiza que los lados A"B" y AB sean paralelos.
$$ \overline{A''B''} \ || \ \overline{AB} $$
Por el teorema de las rectas paralelas, se deduce que los ángulos α≅α" y β≅β" son congruentes, ya que son ángulos correspondientes formados por rectas transversales que cortan a rectas paralelas AB || A"B".
$$ \alpha \cong \alpha '' $$
$$ \beta \cong \beta '' $$
Como inicialmente teníamos β≅β' y α≅α', se concluye que α'≅α" y β'≅β".
$$ \alpha ' \cong \alpha '' $$
$$ \beta ' \cong \beta '' $$
Por lo tanto, según los criterios de congruencia de triángulos, los triángulos A"B"C y A'B'C' son congruentes, lo que establece su semejanza, ya que A'B'C' es congruente a un triángulo homotético de ABC.
3) Conclusión
En síntesis, tanto si los lados AB y A'B' son congruentes como si no, queda demostrada la semejanza de los triángulos ABC y A'B'C', lo que valida el primer criterio de semejanza entre triángulos.
De este modo, disponemos de una demostración completa de la semejanza de triángulos.
Y así sucesivamente.