Segundo Criterio de Semejanza de Triángulos
Dos triángulos se consideran semejantes si tienen dos lados correspondientes proporcionales y el ángulo comprendido entre ellos es congruente.

Dicho de otro modo, si dos triángulos presentan lados en la misma proporción y el ángulo entre esos lados es idéntico, se dice que son figuras semejantes.
A este principio se lo conoce habitualmente como el criterio de semejanza LAL (Lado-Ángulo-Lado).
Ejemplo Ilustrativo
Consideremos, por ejemplo, dos triángulos: ABC y A'B'C'.

Estos triángulos tienen lados proporcionales entre AB y A'B' y entre AC y A'C':
$$ \overline{AB} : \overline{A'B'} = \overline{AC} : \overline{A'C'} $$
Expresado en forma de fracción, esto se traduce en:
$$ \frac{ \overline{AB} }{ \overline{A'B'}} = \frac{ \overline{AC} }{ \overline{A'C'}} $$
Dado que AB = 3, AC = 2, A'B' = 6 y A'C' = 4, se verifica:
$$ \frac{ 3 }{ 6} = \frac{ 2 }{ 4} $$
$$ \frac{ 1 }{ 2} = \frac{ 1 }{ 2} $$
Además, comparten un ángulo congruente α≅α', que en ambos casos es recto:
$$ \alpha \cong \alpha' $$
Aplicando el segundo criterio de semejanza, se concluye que los triángulos ABC y A'B'C' son semejantes.
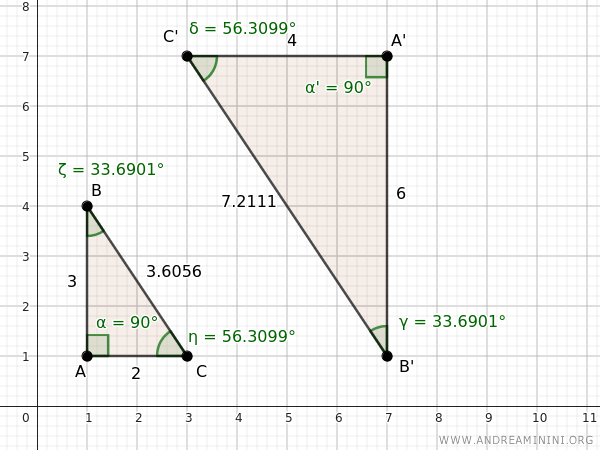
En efecto, su semejanza se confirma por la igualdad de sus ángulos y la proporcionalidad de sus lados correspondientes.
Demostración
Analicemos los triángulos ABC y A'B'C'.
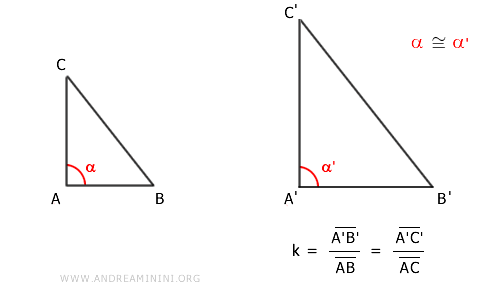
Primero se observa que los lados AB y AC del triángulo ABC son proporcionales a los lados A'B' y A'C' del triángulo A'B'C':
$$ \overline{A'B'} : \overline{AB} = \overline{A'C'} : \overline{AC} $$
Lo que se puede expresar así:
$$ \frac{\overline{A'B'}}{\overline{AB}} = \frac{\overline{A'C'}}{\overline{AC}} = k $$
Además, el ángulo α comprendido entre los lados AB y AC coincide con el ángulo α' comprendido entre los lados A'B' y A'C':
$$ \alpha \cong \alpha' $$
Queremos demostrar que estos dos triángulos son semejantes:
$$ ABC \approx A'B'C' $$
Para ello, analizaremos si los lados AB y A'B' son o no congruentes.
1) Cuando los lados AB y A'B' son congruentes
Si los lados AB y A'B' son congruentes, se deduce de nuestra hipótesis que los lados AC y A'C' también lo serán.
$$ \overline{AB} : \overline{A'B'} = \overline{AC} : \overline{A'C'} $$
Nota: Que AB y A'B' sean congruentes implica que la razón AB/A'B' es igual a 1. $$ 1 = \overline{AC} : \overline{A'C'} $$ Multiplicando ambos términos por A'C' obtenemos: $$ \overline{A'C'} = \overline{AC} $$ Es decir, los lados AC y A'C' son congruentes, es decir, AC ≅ A'C'.
Una vez establecido que los lados AB ≅ A'B' y AC ≅ A'C' son congruentes, por el primer criterio de congruencia de triángulos se concluye que los triángulos ABC y A'B'C' son congruentes.
$$ ABC \cong A'B'C' $$
Y dado que figuras congruentes son, por definición, semejantes con razón de semejanza igual a 1, se confirma que ambos triángulos son semejantes:
$$ ABC \approx A'B'C' $$
2) Cuando los lados AB y A'B' no son congruentes
Si los lados AB y A'B' no son congruentes, calculamos su razón:
$$ k = \frac{\overline{A'B'}}{AB} $$
Una homotecia centrada en A con razón k genera un nuevo triángulo AB"C".
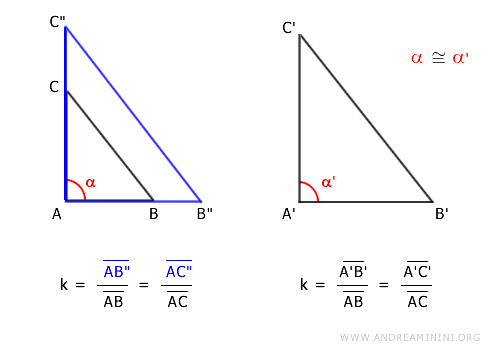
Nota: Se eligió el punto A como centro de homotecia para simplificar la demostración, ya que permite conservar el ángulo α sin alteraciones. Elegir otro punto habría conducido al mismo resultado, aunque con una exposición más extensa.
En este nuevo triángulo, el punto A permanece como punto fijo durante toda la transformación.
La construcción garantiza que los lados AB a AB" y AC a AC" sean proporcionales con razón k:
$$ \frac{\overline{AB"}}{\overline{AB}} = \frac{\overline{AC"}}{\overline{AC}} = k $$
Dado que inicialmente se cumple:
$$ \frac{\overline{A'B'}}{\overline{AB}} = \frac{\overline{A'C'}}{\overline{AC}} = k $$
se deduce que los segmentos A'B' y AB" son congruentes, al igual que A'C' y AC":
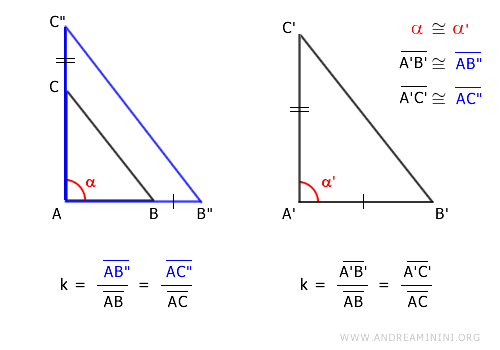
Con la hipótesis inicial que asegura también la congruencia del ángulo α ≅ α',
los triángulos A'B'C' ≅ AB"C" resultan congruentes, según el primer criterio de congruencia de triángulos, ya que tienen dos lados congruentes (A'B' ≅ AB" y A'C' = AC") y el ángulo comprendido congruente (α ≅ α').
$$ A'B'C' \cong AB"C" $$
Como el triángulo AB"C" es semejante al triángulo ABC (toda homotecia es una transformación de semejanza),
$$ AB"C" \approx ABC $$
Explicación: Una semejanza geométrica puede entenderse como la combinación de una homotecia y una isometría. Así, cualquier homotecia produce una figura semejante a la original. Por tanto, el triángulo AB"C" es semejante al triángulo ABC. $$ AB"C" \approx ABC $$
Dado que A'B'C' es congruente con AB"C", se concluye que el triángulo A'B'C' es semejante al triángulo ABC:
$$ A'B'C' \approx ABC $$
3) Reflexión Final
En definitiva, tanto si los lados AB y A'B' son congruentes como si no lo son, se demuestra que los triángulos ABC y A'B'C' cumplen con las condiciones de semejanza.
Así se confirma la validez del segundo criterio de semejanza de triángulos.
Y con esto concluye la demostración.