Criterios de Semejanza para Polígonos con el Mismo Número de Lados

Este resultado, conocido como el Teorema de Semejanza de Polígonos, facilita considerablemente el proceso de establecer la semejanza entre dos polígonos que cuentan con el mismo número n de lados y ángulos.

En otras palabras:

1. El primer criterio permite prescindir de la comprobación de 3 ángulos consecutivos.
2. El segundo criterio excluye 2 ángulos consecutivos y el lado que los une.
3. El tercer criterio omite 1 ángulo y los dos lados adyacentes a él.

Nota. De manera general, para determinar la semejanza entre dos polígonos, se debería verificar la congruencia de todos los ángulos correspondientes y la proporcionalidad entre todos sus lados, lo cual requiere un mayor número de comprobaciones.

Explicación

Decimos que dos polígonos son semejantes cuando tienen la misma forma, aunque no necesariamente el mismo tamaño.

Por tanto, para determinar si dos polígonos con n ángulos y lados son semejantes, deben cumplirse las dos condiciones esenciales de semejanza:

• todos los ángulos correspondientes son congruentes (es decir, tienen la misma amplitud)
• todos los lados correspondientes son proporcionales (es decir, la razón entre lados homólogos en ambos polígonos es constante)

Nota. La simple congruencia de los ángulos correspondientes no basta para establecer la semejanza en polígonos con más de tres lados. Por ejemplo, un cuadrado y un rectángulo tienen ángulos correspondientes congruentes (90°), pero no son figuras semejantes porque sus lados no guardan proporcionalidad constante.

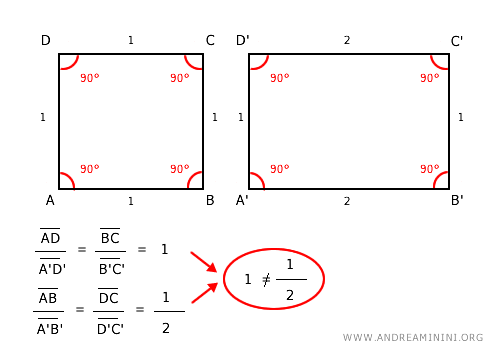
Sin embargo, determinados criterios permiten verificar la semejanza entre dos polígonos con menos información.

En concreto, según el Teorema de Semejanza de Polígonos, cualquiera de los siguientes supuestos basta para establecer semejanza:

• Dos polígonos de n lados son semejantes si tienen n-3 ángulos consecutivos congruentes y todos sus lados correspondientes son proporcionales.

  Nota. Este criterio permite omitir la comprobación de tres ángulos consecutivos. Por ejemplo, en dos pentágonos (n=5), basta verificar la congruencia de n-3 ángulos consecutivos, es decir, de 2 ángulos consecutivos. En el ejemplo, se eligen los ángulos α= α' y β=β'. Además, es imprescindible comprobar que todos los lados correspondientes mantienen la misma razón de proporcionalidad.
  

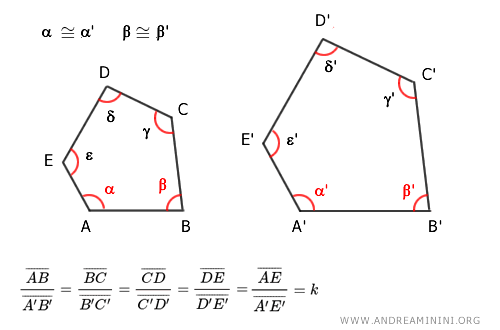
• Dos polígonos de n lados son semejantes si tienen n-2 ángulos consecutivos congruentes y los lados adyacentes a dichos ángulos son proporcionales.

  Nota. Este criterio excluye dos ángulos consecutivos y el lado situado entre ellos. Por ejemplo, en dos pentágonos (n=5), se verifica la congruencia de n-2 ángulos consecutivos, es decir, de 3 ángulos consecutivos. En el ejemplo, se comprueban los ángulos α= α' , β=β' y γ=γ', así como la proporcionalidad de los lados adyacentes. Quedan fuera de la verificación los ángulos δ y ε y el lado DE que los conecta.
  

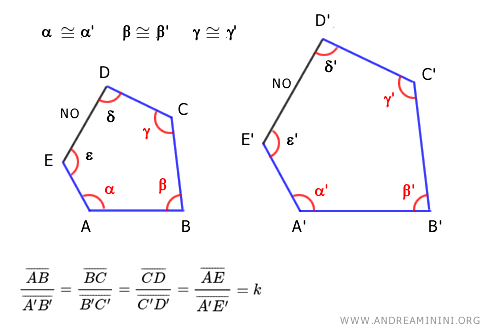
• Dos polígonos de n lados son semejantes si tienen n-1 ángulos correspondientes congruentes y todos los lados que no son adyacentes al ángulo excluido son proporcionales.

  Nota. Este criterio omite un ángulo y los dos lados contiguos a dicho ángulo. Por ejemplo, en un pentágono (n=5), se verifica la congruencia de n-1 ángulos, es decir, de 4 ángulos, y la proporcionalidad únicamente de los lados comprendidos entre ellos. Si se excluye el ángulo ε, basta comprobar la congruencia de los ángulos α≅α' , β≅β' , γ≅γ' y δ≅δ', así como la proporcionalidad de todos los lados, excepto de los lados AE y DE, que son adyacentes al ángulo ε excluido.
  

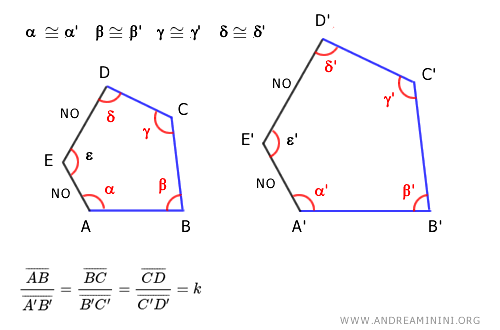
Semejanza en Polígonos Regulares

En el caso de los polígonos regulares, existe un criterio adicional para establecer la semejanza.

Dos polígonos regulares son semejantes si poseen el mismo número n de lados.

Se trata de un corolario directo del Teorema de Semejanza de Polígonos.

Demostración

Partimos de la suposición de tener dos polígonos regulares con n lados.

Por ejemplo, dos pentágonos regulares con n=5 lados, aunque este principio es válido para cualquier valor de n.

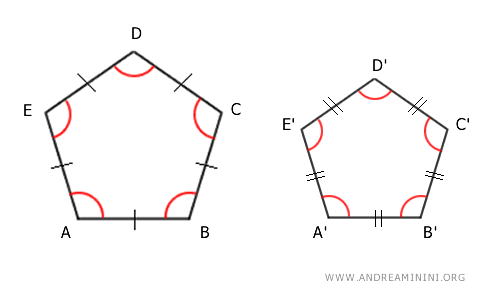
Un polígono se considera «regular» cuando todos sus lados y ángulos son congruentes, es decir, tienen la misma longitud y la misma amplitud, respectivamente.

1] Todos los ángulos congruentes

En cualquier polígono regular, todos sus ángulos internos son, por definición, congruentes, y su amplitud depende únicamente del número n de lados, calculándose mediante la siguiente fórmula:

$$ \frac{n-2}{n} \cdot 180° $$

Esto garantiza que todos los ángulos en un polígono regular tienen exactamente la misma medida.

Por ejemplo, en un pentágono regular con n=5 lados, cada ángulo interno mide 108°.

$$ \frac{n-2}{n} \cdot 180° = \frac{5-2}{5} \cdot 180° = \frac{3}{5} \cdot 180° = 108° $$

Así, si dos polígonos regulares ABCDE y A'B'C'D'E' tienen el mismo número de lados, por ejemplo n=5, se deduce que presentan ángulos correspondientes congruentes e iguales en medida.

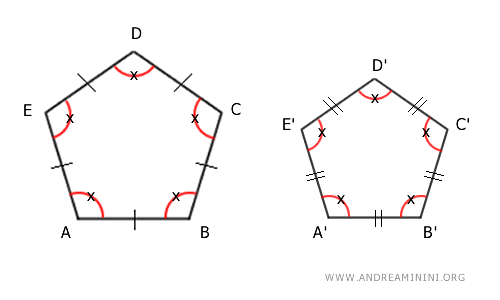
2] Todos los lados congruentes

En un polígono regular, todos sus lados son congruentes, es decir, tienen exactamente la misma longitud.

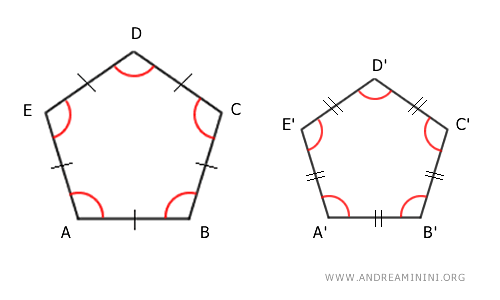
Por tanto, todos los lados del primer polígono ABCDE son congruentes entre sí:

$$ \overline{AB} \cong \overline{BC} \cong \overline{CD} \cong \overline{DE} \cong \overline{EA} $$

Del mismo modo, todos los lados del segundo polígono A'B'C'D'E' son congruentes entre sí:

$$ \overline{A'B'} \cong \overline{B'C'} \cong \overline{C'D'} \cong \overline{D'E'} \cong \overline{A'E'} $$

Si tomamos un par de lados correspondientes de ambos polígonos, por ejemplo AB y A'B', y calculamos su razón de proporcionalidad:

$$ \frac{ \overline{AB}}{ \overline{A'B'} } = k $$

Dado que en cada polígono regular todos los lados son iguales entre sí, se deduce que los demás lados correspondientes mantienen también la misma razón de proporcionalidad k.

Por ejemplo, como AB ≅ BC y A'B' ≅ B'C', la razón entre los lados BC y B'C' es igualmente k.

$$  \frac{ \overline{AB}}{ \overline{A'B'} } = \frac{ \overline{BC}}{ \overline{B'C'} } = k $$

Este mismo razonamiento se extiende al resto de los lados:

$$ \frac{ \overline{CD}}{ \overline{C'D'} } = k $$

$$ \frac{ \overline{DE}}{ \overline{D'E'} } = k $$

$$ \frac{ \overline{EA}}{ \overline{A'E'} } = k $$

Por tanto, si dos polígonos regulares tienen dos lados correspondientes proporcionales, se concluye que todos los demás lados mantienen la misma proporción.

Conclusión

En resumen, en dos polígonos regulares con el mismo número de lados, se cumplen simultáneamente ambas condiciones de semejanza:

1. todos sus ángulos correspondientes son congruentes
2. todos sus lados son proporcionales en una misma razón

Por consiguiente, ambos polígonos son semejantes.

Nota. En otras palabras, cuando se trata de dos polígonos regulares con el mismo número de lados, no es necesario comprobar individualmente la congruencia de sus ángulos ni la proporcionalidad de sus lados. Por definición, en los polígonos regulares todos los ángulos son iguales entre sí y todos sus lados tienen la misma longitud. Así, si dos polígonos de este tipo tienen el mismo número de lados, la congruencia de ángulos y la proporcionalidad de lados quedan automáticamente garantizadas, confirmando su semejanza.

Y así sucesivamente.