Teorema de proporcionalidad entre bases y alturas en triángulos semejantes

En dos triángulos semejantes, la razón entre sus bases es igual a la razón entre sus alturas. Esto significa que ambos elementos varían de forma proporcional.

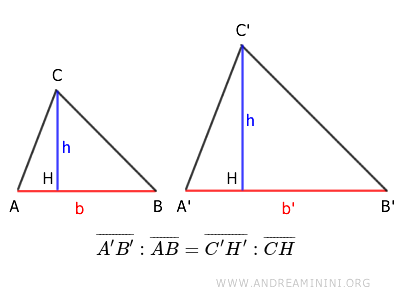
Este resultado es una consecuencia directa del concepto de semejanza: cuando dos triángulos conservan la misma forma, no solo sus lados guardan proporción, sino también sus alturas. Comprender esta relación es fundamental para resolver numerosos problemas de geometría y para reconocer más rápidamente figuras semejantes.

Ejemplo práctico

Para visualizar la idea, consideremos dos triángulos semejantes ABC y A'B'C'.

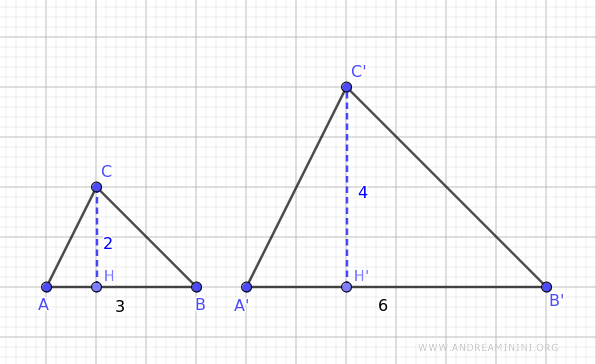
Tomemos AB como base del triángulo ABC y A'B' como base del triángulo A'B'C'. La razón entre estas dos bases es igual a 2:

$$ \frac{ \overline{A'B'} }{ \overline{AB} } = \frac{6}{3} = 2 $$

Si ahora comparamos las alturas correspondientes trazadas sobre esas mismas bases, obtenemos exactamente la misma razón:

$$ \frac{ \overline{C'H'} }{ \overline{CH} } = \frac{4}{2} = 2 $$

La proporción se mantiene. Bases y alturas crecen o disminuyen con la misma escala, lo cual confirma la propiedad.

Nota. Esta relación solo es válida si los triángulos son realmente semejantes.

Si repetimos el razonamiento con otros lados correspondientes, el resultado no cambia. Por ejemplo, usemos BC y B'C' como nuevas bases de referencia, junto con las alturas AH y A'H'.

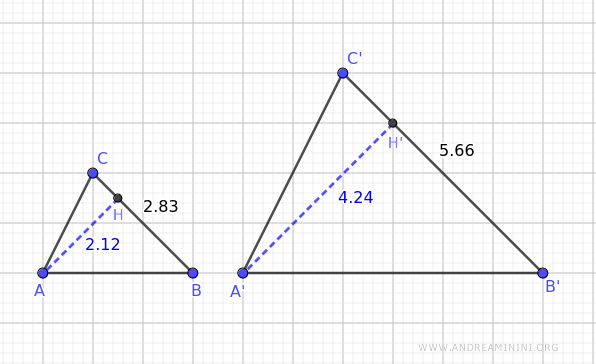
La razón entre estas bases es 1,33:

$$ \frac{ \overline{B'C'} }{ \overline{BC} } = \frac{5.66}{4.24} = 1.33 $$

Y la razón entre las alturas correspondientes también es 1,33:

$$ \frac{ \overline{A'H'} }{ \overline{AH} } = \frac{2.83}{2.12} = 1.33 $$

El resultado coincide de nuevo. Si dos triángulos son semejantes, sus bases siempre guardan la misma relación que sus alturas.

Demostración del teorema

Consideremos ahora la demostración. Sean ABC y A'B'C' dos triángulos semejantes.

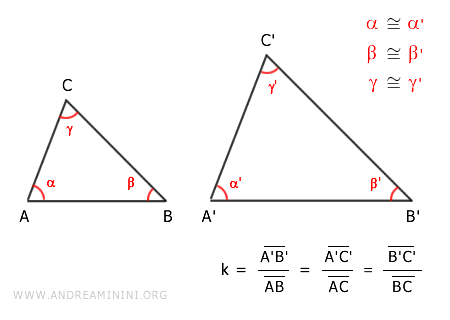
Por definición, los ángulos correspondientes son iguales y los lados guardan una razón constante:

$$ \overline{A'B'} : \overline{AB} = \overline{A'C'} : \overline{AC} = \overline{B'C'} : \overline{BC} $$

Existe, por tanto, un factor de proporcionalidad común \( k \):

$$ \frac{ \overline{A'B'} }{ \overline{AB} } = \frac{ \overline{A'C'} }{ \overline{AC} } = \frac{ \overline{B'C'} }{ \overline{BC} } = k $$

Tomemos de nuevo AB y A'B' como bases. Las alturas correspondientes serán CH y C'H'.

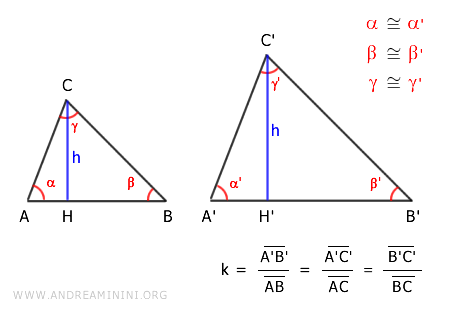
Al trazar las alturas, se forman dos triángulos rectángulos, ACH y A'C'H'. Estos dos triángulos son también semejantes, porque comparten un ángulo correspondiente y mantienen la misma proporción entre sus lados. Aplicando el criterio de semejanza:

$$ ACH \approx A'C'H' $$

De esta semejanza obtenemos la siguiente relación:

$$ \overline{A'C'} : \overline{AC} = \overline{C'H'} : \overline{CH} $$

Dado que AC y A'C' ya guardan la proporción \( k \), se sigue necesariamente que las alturas CH y C'H' también la guardan. En consecuencia:

$$ \overline{A'B'} : \overline{AB} = \overline{C'H'} : \overline{CH} $$

La demostración confirma el enunciado inicial: en los triángulos semejantes, bases y alturas siempre mantienen la misma proporción.