Tercer Criterio de Semejanza de Triángulos
Dos triángulos son semejantes si sus lados correspondientes son proporcionales.
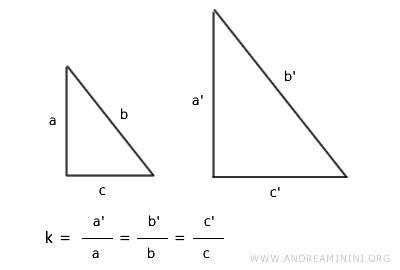
Según este criterio, si dos triángulos tienen sus lados correspondientes en proporción, se dice que son semejantes.
Este método para establecer la semejanza entre triángulos se conoce también como el criterio Lado-Lado-Lado (LLL).
Ejemplo Práctico
Consideremos dos triángulos, ABC y A'B'C', cuyos lados son proporcionales en el mismo orden.
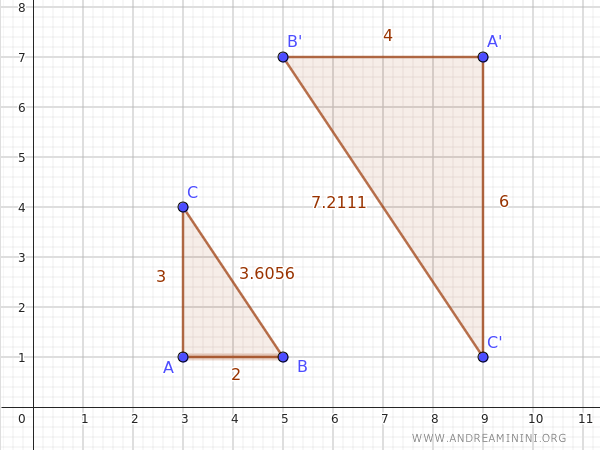
En este caso, la razón de proporcionalidad es 2.
$$ \frac{ \overline{A'B'} }{ \overline{AB} } = \frac{4}{2} = 2 $$
$$ \frac{ \overline{A'C'} }{ \overline{AC} } = \frac{6}{3} = 2 $$
$$ \frac{ \overline{B'C'} }{ \overline{BC} } = \frac{7.2}{3.6} = 2 $$
Por el tercer criterio de semejanza, los triángulos ABC y A'B'C' son semejantes:
$$ ABC \approx A'B'C' $$
Esto significa que ambos triángulos tienen la misma forma, aunque difieren en tamaño.
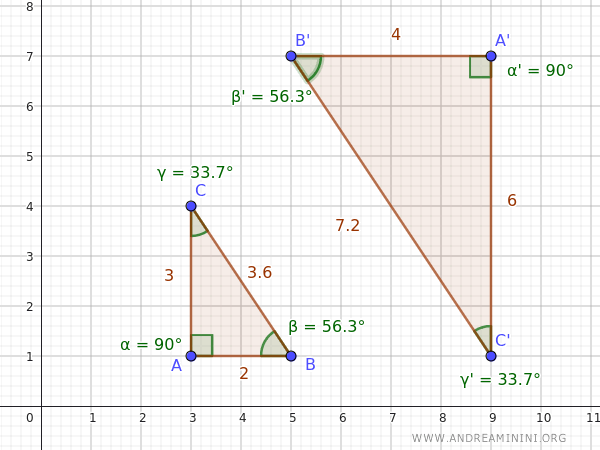
Demostración
Consideremos dos triángulos, ABC y A'B'C'.
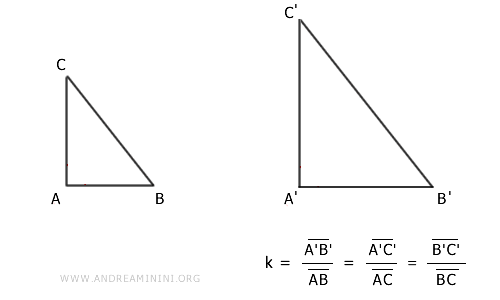
Por hipótesis, sus lados son proporcionales en el mismo orden:
$$ \overline{A'B'}:\overline{AB} = \overline{B'C'}:\overline{BC} = \overline{A'C'}:\overline{AC} $$
Podemos expresar esta proporcionalidad mediante fracciones iguales:
$$ \frac{ \overline{A'B'} }{ \overline{AB} } = \frac{ \overline{B'C'} }{ \overline{BC} } = \frac{ \overline{A'C'} }{ \overline{AC} } = k $$
Donde \( k \) es la razón de semejanza.
Queremos demostrar que los dos triángulos son semejantes:
$$ ABC \approx A'B'C' $$
Analicemos dos casos: cuando los lados AB y A'B' son congruentes y cuando no lo son.
1] Los lados AB y A'B' son congruentes
En este caso, los lados AB y A'B' tienen igual longitud:
$$ \overline{A'B'} \cong \overline{AB} $$
Así, la razón de semejanza es \( k = 1 \).
$$ k = \frac{ \overline{A'B'} }{ \overline{AB} } = 1 $$
Esto implica que los otros lados también cumplen la misma razón:
$$ \frac{ \overline{A'B'} }{ \overline{AB} } = \frac{ \overline{B'C'} }{ \overline{BC} } = \frac{ \overline{A'C'} }{ \overline{AC} } = 1 $$
Por tanto, todos los lados correspondientes son congruentes:
$$ \overline{AB} \cong \overline{A'B'} $$
$$ \overline{BC} \cong \overline{B'C'} $$
$$ \overline{AC} \cong \overline{A'C'} $$
Por el tercer criterio de congruencia de triángulos, los triángulos ABC y A'B'C' son congruentes.
$$ ABC \cong A'B'C' $$
Y, dado que dos figuras congruentes también son semejantes (con \( k = 1 \)), se concluye que ABC y A'B'C' son semejantes.
2] Los lados AB y A'B' no son congruentes
En este caso, los lados AB y A'B' tienen longitudes distintas:
$$ k = \frac{ \overline{A'C'} }{ \overline{AC} } \ne 1 $$
Esto implica que los demás lados correspondientes tampoco son congruentes:
$$ \frac{ \overline{A'B'} }{ \overline{AB} } = \frac{ \overline{B'C'} }{ \overline{BC} } = \frac{ \overline{A'C'} }{ \overline{AC} } = k \ne 1 $$
Para demostrar la semejanza, aplicamos una homotecia al triángulo ABC, tomando como centro el punto A.
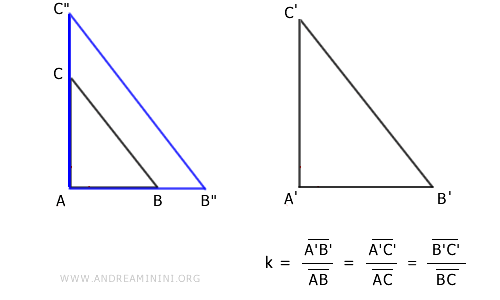
Así obtenemos el triángulo A"B"C", imagen homotética de ABC.
Los triángulos A"B"C" y ABC son semejantes, ya que toda homotecia produce una figura semejante.
$$ A"B"C" \approx ABC $$
Elegimos la razón de homotecia \( k \) idéntica a la razón de semejanza entre los lados de ABC y A'B'C':
$$ \frac{ \overline{A'B'} }{ \overline{AB} } = \frac{ \overline{B'C'} }{ \overline{BC} } = \frac{ \overline{A'C'} }{ \overline{AC} } = k $$
Así, los lados correspondientes de A"B"C" y A'B'C' tienen la misma longitud.
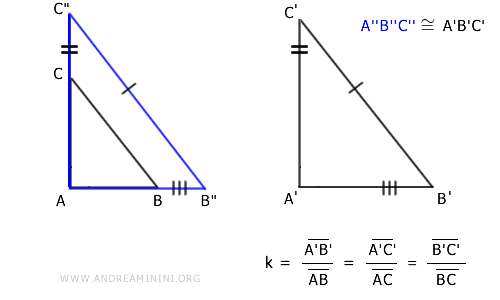
Por el tercer criterio de congruencia de triángulos, A"B"C" y A'B'C' son congruentes:
$$ A'B'C' \cong A''B''C'' $$
Y al ser congruentes, también son semejantes con \( k = 1 \):
$$ A'B'C' \approx A''B''C'' $$
Como A'B'C' es semejante a ABC (pues es una imagen homotética de éste), se deduce que A'B'C' y ABC son semejantes:
$$ A'B'C' \approx A''B''C'' \approx ABC $$
Por tanto, incluso en este caso, los triángulos A'B'C' y ABC son semejantes.
3) Conclusión
En ambos escenarios, tanto si los lados AB y A'B' son congruentes como si no, los triángulos ABC y A'B'C' resultan ser semejantes.
Esto demuestra el tercer criterio de semejanza de triángulos.
Y así queda demostrado.