Teorema del Radio de la Circunferencia Circunscrita en Polígonos Regulares Semejantes
En dos polígonos regulares semejantes con el mismo número de lados, no solo sus lados son proporcionales, sino que también los radios de sus circunferencias circunscritas y sus apotemas mantienen la misma proporción.
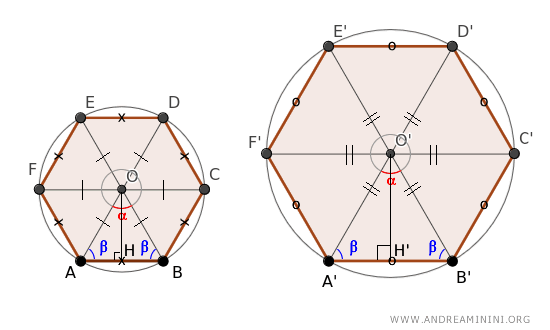
Este teorema demuestra que, cuando se comparan dos polígonos regulares semejantes con idéntico número de lados, existe una razón constante no solo entre sus lados, sino también entre los radios de las circunferencias que los circunscriben y sus apotemas.
En otras palabras, la proporcionalidad que existe entre los lados de ambos polígonos se refleja igualmente en la relación entre los radios de sus circunferencias circunscritas y sus apotemas.
Corolario. Dado que dos polígonos regulares con el mismo número de lados tienen sus perímetros en la misma proporción (véase el teorema sobre perímetros de polígonos semejantes), se deduce que los radios de sus circunferencias circunscritas y sus apotemas están en la misma proporción que los lados y los perímetros de los polígonos.
Ejemplo Ilustrativo
Tomemos como ejemplo dos hexágonos regulares semejantes.
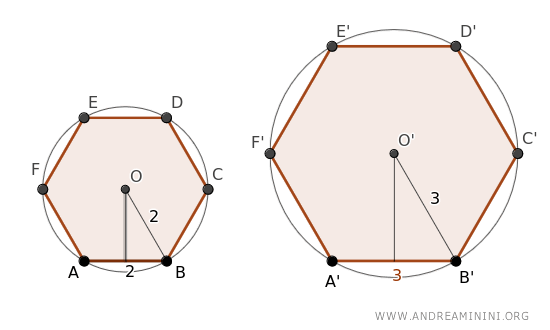
El primer hexágono tiene lados de longitud 2, mientras que el segundo tiene lados de longitud 3.
$$ AB = BC = CD = DE = EF = FA = 2 $$
$$ A'B' = B'C' = C'D' = D'E' = E'F' = A'F' = 3 $$
Al ser polígonos regulares, ambos pueden estar circunscritos por una circunferencia, cuyos radios son 2 y 3, respectivamente.
$$ OB = 2 $$
$$ O'B' = 3 $$
Se observa claramente que los radios mantienen la misma proporción que los lados:
$$ OB : O'B' = AB : A'B' $$
$$ 2 : 3 = 2 : 3 $$
$$ 0.6666 = 0.6666 $$
Aquí, la razón de proporcionalidad se mantiene constante en 0.6666.
Para calcular los apotemas, hallamos los catetos de los triángulos rectángulos OBH y O'B'H', aplicando el teorema de Pitágoras.
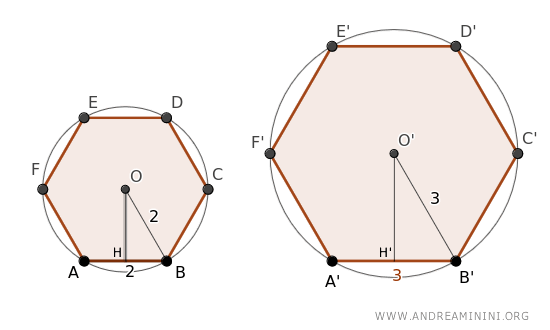
Los triángulos rectángulos tienen lados OB = 2 y HB = 1, y O'B' = 3 y H'B' = 1.5
$$ OH = \sqrt{2^2 - 1^2} = \sqrt{3} $$
$$ O'H' = \sqrt{3^2 - 1.5^2} = \sqrt{6.75} $$
Los segmentos OH y O'H' representan los apotemas de ambos hexágonos.
Por último, calculamos la razón entre estos segmentos:
$$ \frac{ \sqrt{3} }{ \sqrt{6.75} } = 0.6666 $$
La razón de proporcionalidad entre los apotemas coincide exactamente con la existente entre los radios de las circunferencias circunscritas y los lados de los polígonos.
Demostración del Teorema
Consideremos dos polígonos regulares con el mismo número de lados.
Imaginemos, por ejemplo, dos hexágonos de distinto tamaño.
Al tratarse de polígonos regulares con el mismo número de lados, se consideran semejantes según el teorema de semejanza de polígonos regulares.
Por tanto, todos sus lados mantienen la misma proporción:
$$ AB:A'B' = BC:B'C' = CD:C'D' = DE:D'E' = EF:E'F' = FA:A'F' $$
Además, al ser polígonos regulares, cada uno puede estar circunscrito por una circunferencia.
Si se trazan segmentos desde el centro O hacia cada vértice de los hexágonos,
dichos segmentos son iguales dentro de cada polígono, pues corresponden al radio de la circunferencia circunscrita.
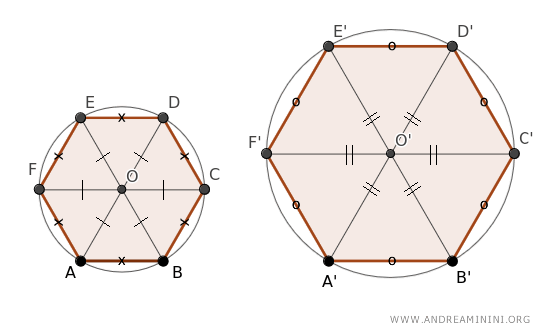
Este procedimiento divide cada hexágono en seis triángulos.
Todos esos triángulos son isósceles porque los lados inclinados coinciden con el radio de sus respectivas circunferencias.
Además, según el tercer criterio de congruencia de triángulos, los triángulos que conforman cada polígono son congruentes, ya que todos sus lados son iguales entre sí.
$$ ABO \cong BCO \cong CDO \cong DEO \cong EFO \cong FAO $$
$$ A'B'O' \cong B'C'O' \cong C'D'O' \cong D'E'O' \cong E'F'O' \cong F'A'O' $$
Asimismo, en ambos polígonos, el ángulo central se divide en seis partes iguales:
$$ \alpha = \frac{360°}{6} = 60° $$
Por lo tanto, cada triángulo de ambos polígonos presenta un ángulo en el vértice O (α = 60°).
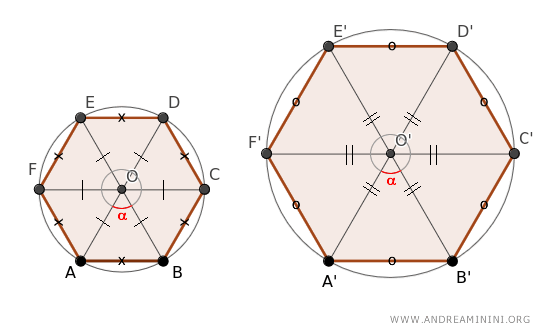
Aplicando el segundo criterio de semejanza de triángulos, los triángulos del primer polígono son semejantes a los del segundo, ya que poseen un ángulo congruente y lados proporcionales.
Si nos centramos, por sencillez, en los triángulos ABO y A'B'O':
$$ ABO \approx A'B'O' $$
Esto demuestra que todos los lados de ambos triángulos son proporcionales:
$$ AB:A'B' = OB:O'B' = OA:O'A' $$
Donde AB y A'B' son lados de los polígonos, y OA y O'A' representan los radios de las circunferencias circunscritas.
Así queda probado que los radios de las circunferencias circunscritas guardan con los lados de los polígonos regulares la misma proporción.
Nota. Los triángulos ABO y A'B'O' son isósceles semejantes, por lo que todos sus lados son proporcionales. En consecuencia, las alturas relativas a sus bases AB y A'B' - es decir, los apotemas de los polígonos - también mantienen dicha proporción: $$ OH:O'H' = OA:O'A' = AB:A'B' $$
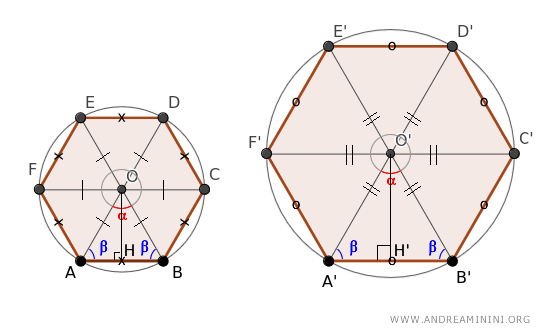
Para comprobarlo, basta recordar que en los triángulos isósceles los ángulos de la base son congruentes. Como el ángulo del vértice es congruente (α), los triángulos ABO y A'B'O' tienen ángulos de base iguales $$ \beta = \frac{180° - \alpha}{2} $$. Si dividimos estos triángulos isósceles en dos triángulos rectángulos AOH y A'O'H, estos también son semejantes, porque, según el segundo criterio de semejanza de triángulos, tienen lados proporcionales OA:O'A' = AH:A'H' y comparten el ángulo β. Por tanto, las alturas también mantienen la misma proporción: $$ OH:O'H' = OA:O'A' $$ Esto demuestra que el apotema del polígono guarda la misma relación de proporcionalidad que el radio de la circunferencia circunscrita y el lado del polígono.
Y así sucesivamente.