Polígonos Regulares

Los polígonos regulares son figuras geométricas planas cuyos lados y ángulos son todos iguales.

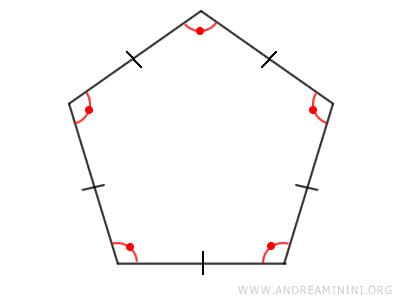
En términos sencillos, un polígono regular es equilátero y equiángulo al mismo tiempo, es decir, todos sus lados miden lo mismo y todos sus ángulos internos tienen la misma amplitud.

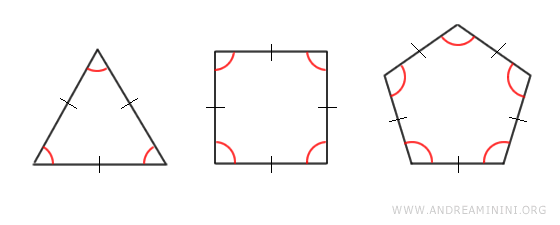
Ejemplos. Algunos ejemplos frecuentes de polígonos regulares son el triángulo equilátero, el polígono regular más simple, con tres lados iguales y ángulos de 60°, y el cuadrado, que tiene cuatro lados iguales y cuatro ángulos rectos.

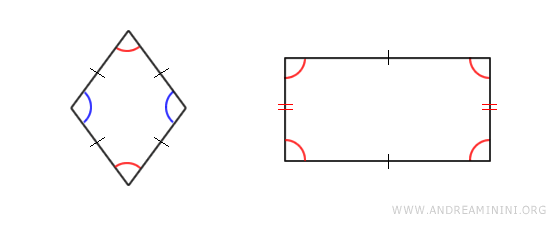
Por el contrario, un rombo no es un polígono regular, ya que aunque tiene lados iguales, sus ángulos no son iguales. Del mismo modo, un rectángulo tampoco es un polígono regular, porque aunque todos sus ángulos son rectos, sus lados no tienen la misma longitud.

Medida de los Ángulos

En un polígono regular de n lados, conocido como n-ágono, cada ángulo interior mide lo mismo (α), y se puede calcular mediante la siguiente fórmula:

$$ \alpha = (n−2) \cdot \frac{180°}{n} $$

Por ejemplo, en un hexágono regular (n = 6 lados), cada ángulo interior mide 120°.

$$ \alpha = (6−2) \cdot \frac{180°}{6} = 4 \cdot 30° = 120° $$

Círculos Inscrito y Circunscrito de los Polígonos Regulares

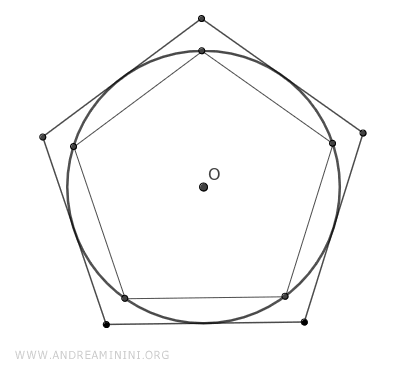
Un polígono regular puede inscribirse en un círculo exterior y circunscribirse alrededor de un círculo interior, teniendo ambos el mismo centro (O), conocido como el centro del polígono.

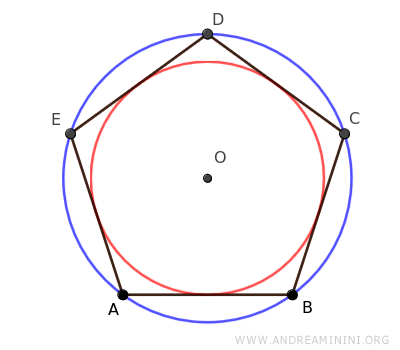
En otras palabras, todos los polígonos regulares pueden inscribirse en una circunferencia, lo que significa que todos sus vértices se apoyan sobre ella.

El radio del círculo circunscrito (azul) coincide con la distancia entre el centro del polígono y cualquiera de sus vértices, y recibe el nombre de radio del polígono regular.

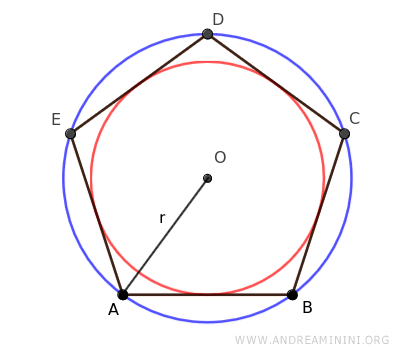
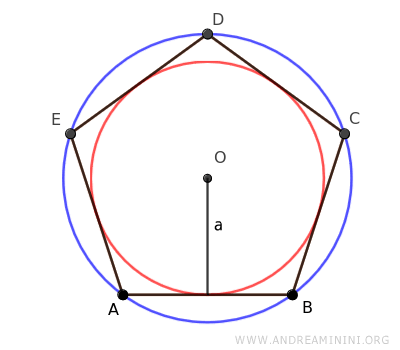
Asimismo, los polígonos regulares pueden circunscribirse alrededor de un círculo interior (rojo), de forma que todos sus lados sean tangentes a dicha circunferencia.

El radio de este círculo inscrito se denomina apotema (a).

Demostración

Vamos a partir de un polígono regular. Por ejemplo, un pentágono.

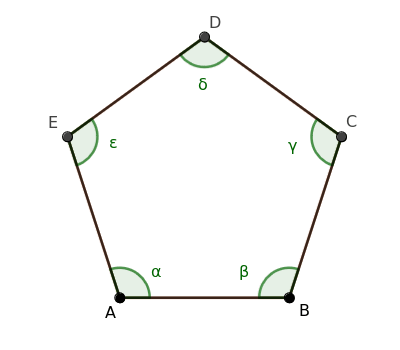
Al tratarse de un polígono regular, es simultáneamente equilátero y equiángulo.

$$ \overline{AB} \cong \overline{BC} \cong \overline{CD} \cong \overline{DE} \cong \overline{EA} $$

$$ \alpha \cong \beta \cong \gamma \cong \delta \cong \epsilon $$

Queremos demostrar que puede inscribirse en un círculo exterior y circunscribirse alrededor de un círculo interior, y que ambos comparten el mismo centro.

Para ello, trazamos las bisectrices de los ángulos α y β, dividiéndolos en dos partes iguales, α'≅α'' y β'≅β''.

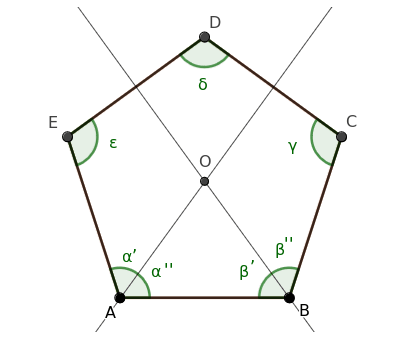
Sea O el punto donde se intersectan estas dos bisectrices.

Como α≅β son ángulos congruentes (según nuestra hipótesis inicial), sus mitades también lo son: α'≅α''≅β'≅β''.

$$ \alpha' = \alpha'' \cong \beta' = \beta'' $$

En consecuencia, el triángulo ABO es un triángulo isósceles, ya que posee dos ángulos congruentes (α''≅β') en su base.

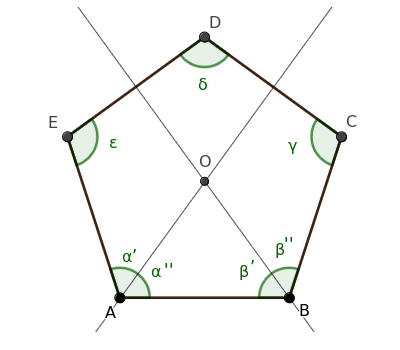
Todo triángulo isósceles tiene dos lados iguales, por lo que los segmentos OA≅OB son congruentes.

$$ \overline{OA} \cong \overline{OB} $$

Después, trazamos el segmento OC, que une el punto O con el vértice C del polígono regular.

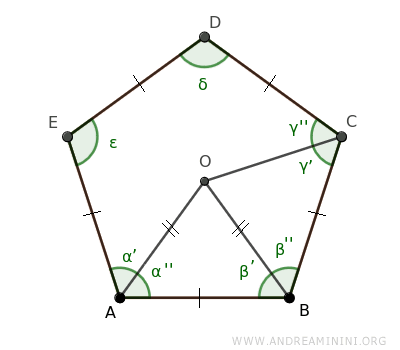
Los triángulos ABO y BCO son congruentes según el primer teorema de congruencia de triángulos, ya que comparten el lado BO, tienen un lado congruente (AB≅BC) y presentan ángulos congruentes por construcción (β'≅β'').

Por tanto, los triángulos ABO y BCO son congruentes en todos sus lados y ángulos.

Esto implica que los segmentos OC≅OB y los ángulos α''≅γ' son congruentes.

$$ \overline{OC} \cong \overline{OB} $$

$$ \alpha'' \cong \gamma' $$

Como sabemos que α''≅γ' y α''≅α', por la propiedad transitiva podemos concluir que α'≅α''≅γ'.

$$ \alpha' \cong \alpha'' \cong \gamma' $$

Dado que α≅γ según la hipótesis inicial, y que α'+α'' = α/2 debido a la construcción de la bisectriz, podemos deducir que γ'+γ'' = γ/2.

Por lo tanto, γ'≅γ'' y el segmento OC es la bisectriz del ángulo γ.

$$ \gamma' \cong \gamma'' $$

Podemos repetir este mismo procedimiento para los demás vértices del polígono regular (D, E), encontrando que los triángulos OCD≅ODE≅OEA también resultan congruentes y son isósceles.

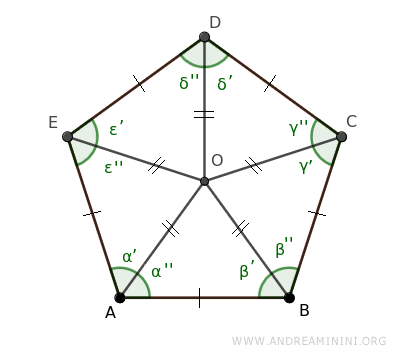
Como resultado, los segmentos OA, OB, OC, OD y OE son todos congruentes.

$$ \overline{OA} \cong \overline{OB} \cong \overline{OC} \cong \overline{OD} \cong \overline{OE} $$

Esto significa que el punto O se encuentra a la misma distancia de los vértices A, B, C, D y E del polígono regular.

Si O está equidistante de todos los vértices, podemos trazar una circunferencia que pase exactamente por todos ellos.

Así se obtiene la circunferencia circunscrita del polígono.

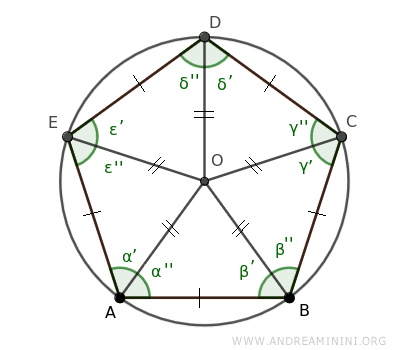
Además, el punto O es el punto de intersección de todas las bisectrices de los triángulos isósceles OAB, OBC, OCD, ODE y OEA.

Como los puntos situados sobre la bisectriz de un ángulo están a igual distancia de sus lados, podemos concluir que O está a la misma distancia de todos los lados de los triángulos OAB, OBC, OCD, ODE y OEA.

Por tanto, si se traza una circunferencia con centro en O y radio igual a la distancia de O a cualquiera de los lados de estos triángulos, dicha circunferencia será tangente a todos los lados del polígono regular.

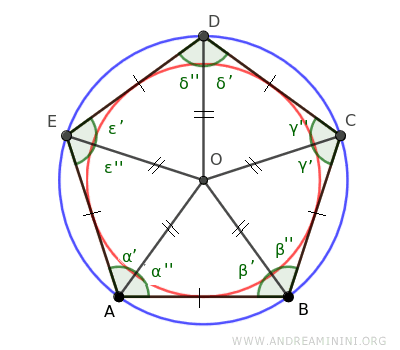
De esta forma se obtiene el círculo interior que queda inscrito en el polígono.

Además, los círculos inscrito y circunscrito comparten el mismo centro O.

Con esto queda demostrada la proposición inicial.

Apotema

La apotema es la distancia más corta que hay entre el centro del polígono y cualquiera de sus lados, y coincide con el radio del círculo inscrito en un polígono regular.

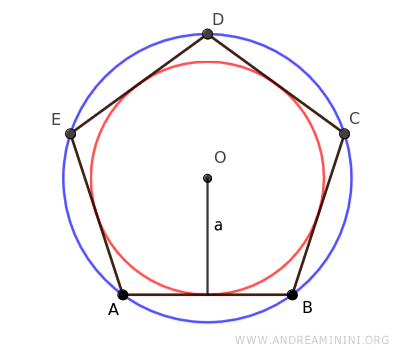
Este valor resulta especialmente útil para calcular el área de un polígono regular.

El área (A) de un polígono regular se obtiene multiplicando el perímetro (P) por la apotema (a) y dividiendo entre dos:

$$ A = \frac{P \cdot a}{2} $$

Ejemplo. Consideremos un pentágono cuyos lados miden 3 y cuya apotema es a=2.06. Primero calculamos el perímetro: $$ P = 3 \cdot 5 = 15 $$ Luego, con la apotema a=2.06, hallamos el área del pentágono: $$ A = \frac{P \cdot a}{2} = \frac{15 \cdot 2.06}{2} = 15.45 $$ Por lo tanto, el área del pentágono es A=15.45.

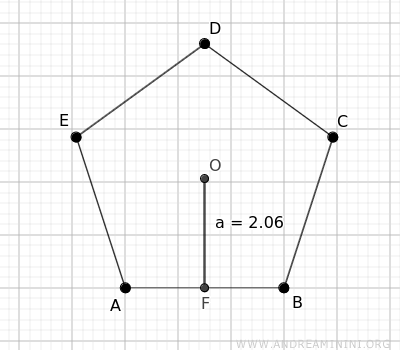
Área de un Polígono Regular

El área de un polígono regular se calcula multiplicando el semiperímetro (p) por la apotema (a): $$ A = p \cdot a $$

La apotema es el segmento que une el centro del polígono con el punto medio de uno de sus lados, mientras que el semiperímetro es la mitad del perímetro, es decir, 2p = P, por lo que p = P/2.

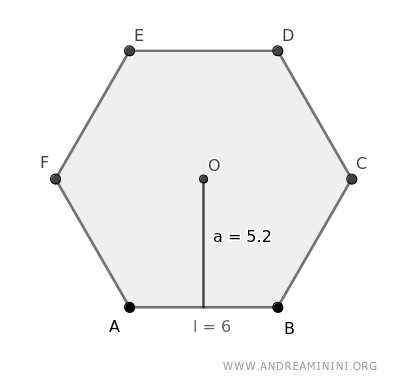
Esto se debe a que cualquier polígono regular puede descomponerse en varios triángulos iguales.

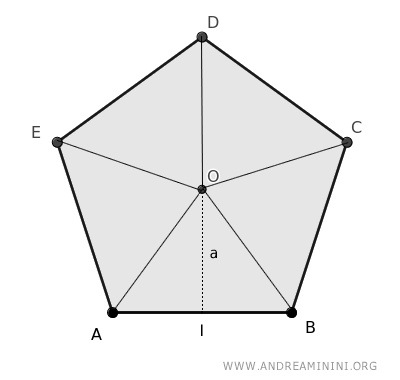
El área de cada uno de estos triángulos se obtiene multiplicando la base por la altura y dividiendo entre dos; en este caso, la base es el lado del polígono y la altura es la apotema.

La suma de las áreas de todos esos triángulos equivale al área total del polígono regular.

Radio de un Polígono Regular

El radio de un polígono regular es el segmento que une el centro del polígono con cualquiera de sus vértices.

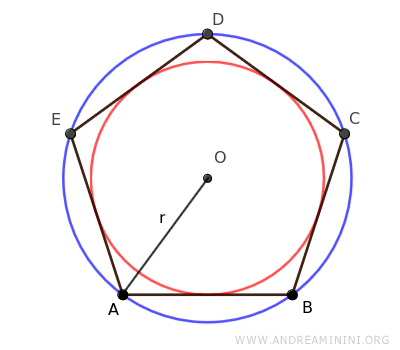
Este radio coincide con el del círculo circunscrito alrededor del polígono, pues todos los vértices de un polígono regular se encuentran sobre una circunferencia cuyo centro (O) es también el centro del polígono.

Una propiedad interesante es que, en un polígono regular, todos los radios son congruentes, es decir, tienen exactamente la misma longitud.

Observaciones Adicionales

A continuación, algunos datos y curiosidades sobre los polígonos regulares:

• Simetría
  Todo polígono regular posee simetría radial y axial. El número de ejes de simetría coincide con su número de lados.
• Diagonales
  El número de diagonales D en un polígono regular se calcula mediante la fórmula: $$ D = \frac{n(n-3)}{2} $$ donde n es el número de lados.

  Ejemplo. Un pentágono tiene n=5 lados, por lo que tiene D=5 diagonales: $$ D = 5 \cdot (5-3)/2 = 5 \cdot 2/2 = 5 $$ Para comprobarlo, basta dibujar todas las diagonales posibles que unen los vértices del pentágono. Se obtienen 5 diagonales.
  

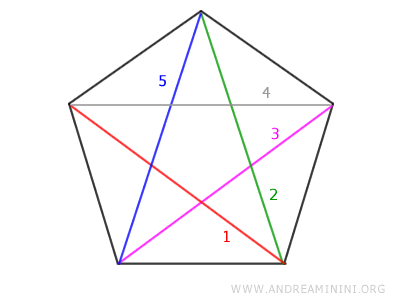
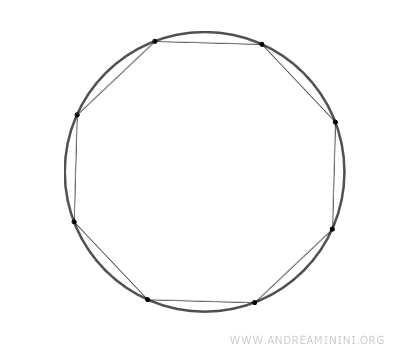
• A medida que aumenta el número de lados, los polígonos regulares se parecen cada vez más a un círculo. No obstante, siguen siendo polígonos con lados definidos, por muchos que sean.
  
• Círculos Inscrito y Circunscrito
  Un polígono regular siempre puede inscribirse en una circunferencia y circunscribirse alrededor de otra.
  

  Nota. En el caso particular de un hexágono regular, el lado del hexágono siempre coincide con el radio del círculo inscrito.

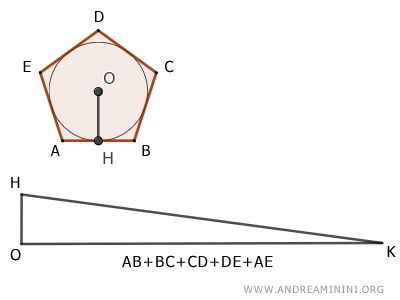
• Equivalencia entre un Polígono Regular y un Triángulo
  El área de un polígono regular es igual al área de un triángulo cuya base equivale al perímetro del polígono y cuya altura es la apotema.
  
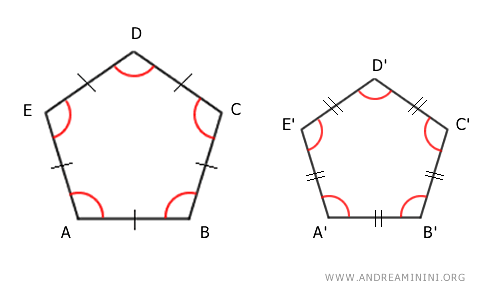
• Dos Polígonos Regulares con el Mismo Número de Lados son Semejantes
  Este criterio facilita enormemente verificar la semejanza entre dos polígonos cuando ambos son regulares y tienen el mismo número de lados.
  

Y así sucesivamente.