Cuadriláteros

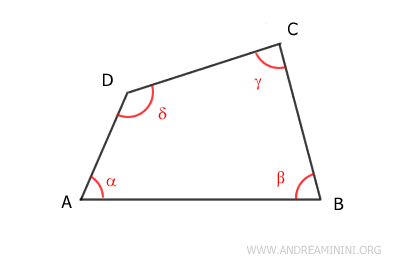
Un cuadrilátero es un polígono formado por cuatro lados.

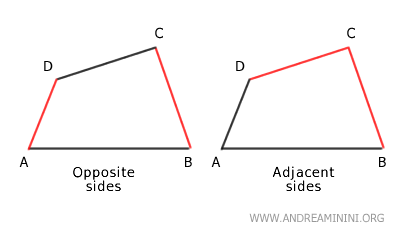
Los lados de un cuadrilátero pueden clasificarse en:

• Lados adyacentes
  cuando comparten un mismo vértice.
• Lados opuestos
  cuando no comparten ningún vértice.

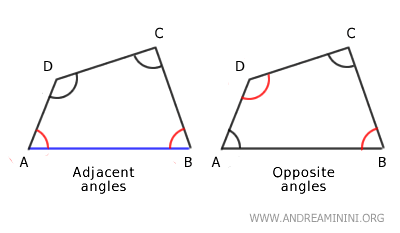
Los ángulos de un cuadrilátero pueden ser:

• Ángulos adyacentes
  cuando comparten un mismo lado.
• Ángulos opuestos
  cuando no tienen lados en común.

Todo cuadrilátero posee dos diagonales que unen vértices situados en ángulos opuestos.

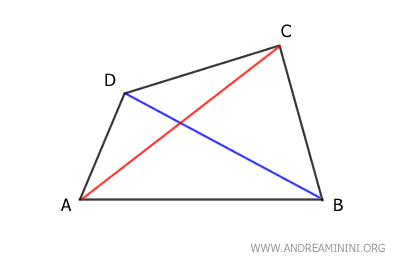
Nota: Una diagonal divide un cuadrilátero en dos triángulos. Dado que la suma de los ángulos interiores de un triángulo es 180°, y un cuadrilátero está compuesto por dos triángulos, la suma de los ángulos interiores de cualquier cuadrilátero es 360°. 

La suma de los ángulos interiores de un cuadrilátero siempre es 360° (un ángulo completo).

$$ \alpha + \beta + \gamma + \delta = 360° $$

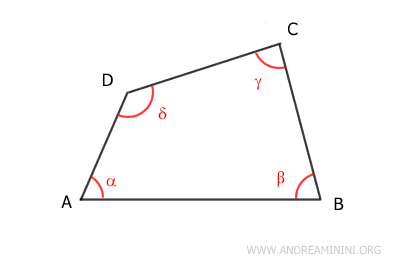
Tipos de Cuadriláteros

Según su forma, los cuadriláteros pueden clasificarse en:

• Cuadriláteros convexos
  Todos sus ángulos interiores miden menos de 180°, lo que implica que sus diagonales quedan completamente dentro de la figura.
  
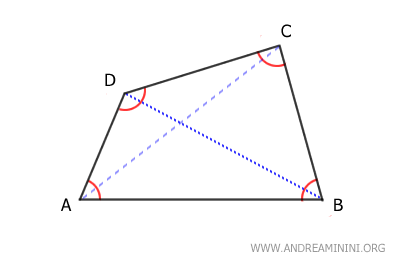
  Entre los cuadriláteros convexos se incluyen los trapecios, los paralelogramos y las cometas convexas.
  • Trapecios
    Son cuadriláteros que tienen un único par de lados paralelos. Pueden ser escalenos, isósceles o rectángulos.
    
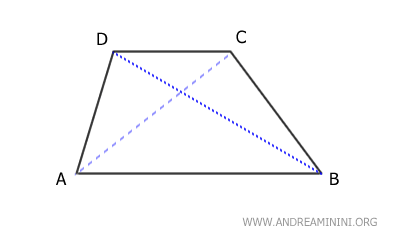
  • Paralelogramos
    Son cuadriláteros cuyos lados opuestos son paralelos y de la misma longitud.
    
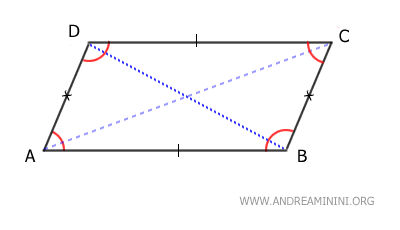
    Dentro de los paralelogramos se encuentran el rectángulo, el rombo y el cuadrado.
    • Rectángulos
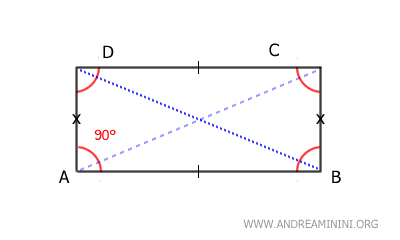
      Son paralelogramos cuyos ángulos interiores miden 90°.
      
    • Rombos
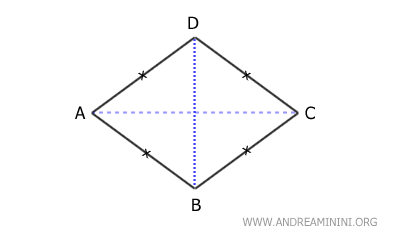
      Son paralelogramos cuyos cuatro lados miden lo mismo y cuyas diagonales son perpendiculares entre sí.
      
    • Cuadrados
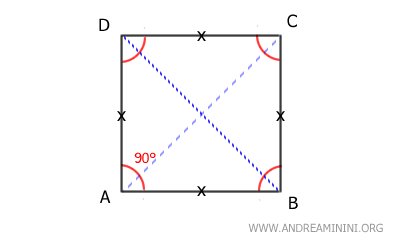
      Son paralelogramos que tienen todos sus lados iguales, sus ángulos rectos y diagonales perpendiculares. En definitiva, el cuadrado combina las propiedades tanto del rectángulo como del rombo.
      
  • Cometas convexas
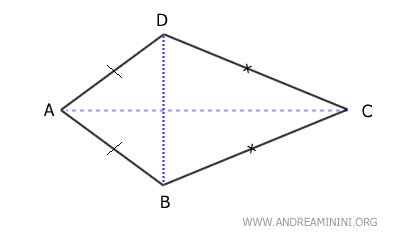
    Son cuadriláteros cuyas diagonales se cruzan perpendicularmente.
    
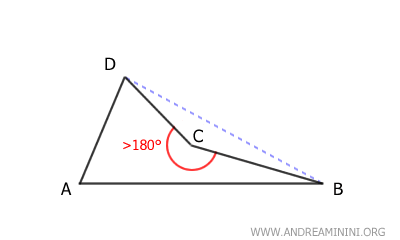
• Cuadriláteros cóncavos
  En estos cuadriláteros, al menos uno de sus ángulos interiores supera los 180°, lo que provoca que al menos una de sus diagonales quede fuera de la figura.
  

Notas Adicionales

Algunos aspectos importantes sobre los cuadriláteros:

• El perímetro de un cuadrilátero es la suma de la longitud de todos sus lados.
• Cada lado de un cuadrilátero es siempre menor que la suma de los otros tres lados.
• Área de un cuadrilátero con diagonales perpendiculares
  El área de un cuadrilátero cuyas diagonales se cruzan perpendicularmente se calcula multiplicando las longitudes de las diagonales y dividiendo el resultado entre dos. $$ A = \frac{d_1 \cdot d_2}{2} $$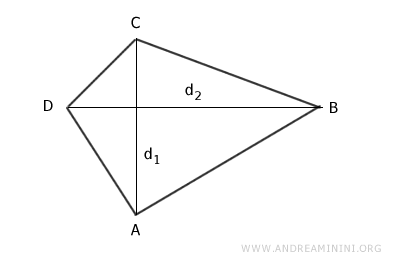

  

• Cuadriláteros circunscritos
  Un cuadrilátero se dice circunscrito a una circunferencia cuando las bisectrices de sus ángulos se intersectan en un único punto, denominado «incentro». Dicha circunferencia, cuyo centro es el incentro (O), es tangente a los cuatro lados del cuadrilátero.
  

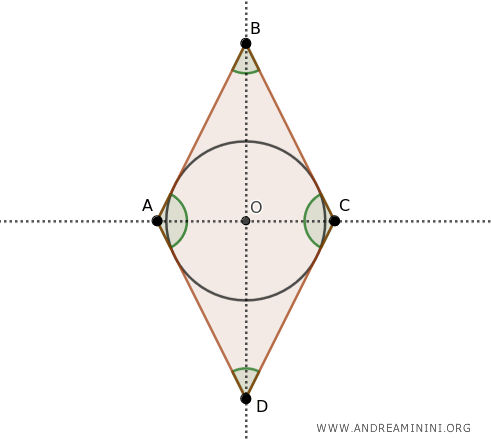
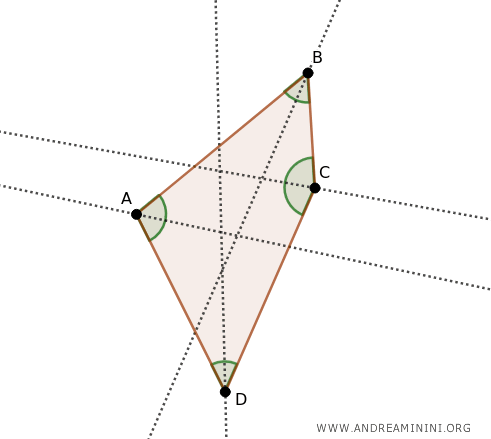
  Por ejemplo, el rombo y el cuadrado son ejemplos de cuadriláteros que pueden circunscribirse, ya que sus bisectrices se cortan en un punto común. Sin embargo, no todos los cuadriláteros cumplen esta condición. A continuación, se muestra un ejemplo de un cuadrilátero que no puede circunscribirse. 
  

  Si un cuadrilátero es circunscrito a una circunferencia, la suma de las longitudes de dos lados opuestos es igual a la suma de las longitudes de los otros dos lados. $$ \overline{AB} + \overline{CD} = \overline{BC} + \overline{AD} $$

Y así sucesivamente...