Rectángulo
Un rectángulo es un tipo de paralelogramo en el que todos sus ángulos son congruentes y rectos.
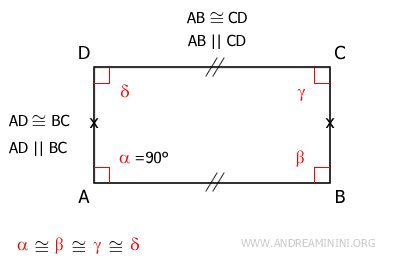
Como ocurre en cualquier paralelogramo, un rectángulo presenta las siguientes propiedades:
- Sus lados opuestos son congruentes y paralelos
- Sus ángulos opuestos son congruentes
- Los ángulos adyacentes sobre un mismo lado son suplementarios
- Sus diagonales se intersectan en el punto medio
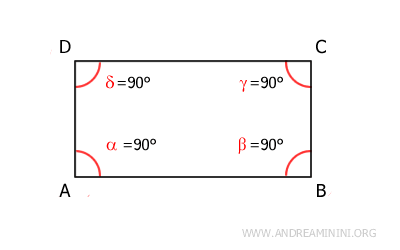
Además, todos los ángulos de un rectángulo son rectos (90°).
Al ser un cuadrilátero, la suma de los ángulos interiores de un rectángulo es de 360°. Como todos sus ángulos son congruentes, cada uno mide necesariamente 90°, pues 360° dividido entre cuatro es 90°.
En un rectángulo, las diagonales son congruentes, es decir, tienen la misma longitud.
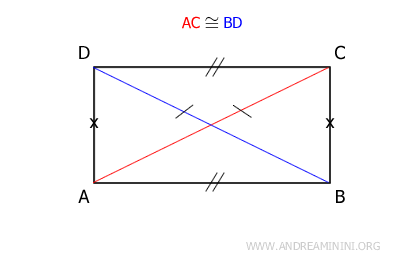
Cada diagonal divide el rectángulo en dos triángulos rectángulos congruentes.
Además, las diagonales dividen el rectángulo en cuatro triángulos isósceles, congruentes dos a dos.
Fórmulas fundamentales de un rectángulo
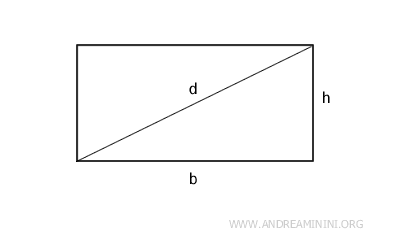
- El perímetro de un rectángulo es el doble de la suma de la base y la altura: $$ P = 2 \cdot (b + h ) $$
- El área de un rectángulo se obtiene multiplicando la base por la altura: $$ A = b \cdot h $$ Consulta la demostración.
- La diagonal es la raíz cuadrada de la suma de los cuadrados de la base y la altura, de acuerdo con el teorema de Pitágoras: $$ d = \sqrt{b^2 + h^2} $$
Base y altura de un rectángulo
La base y la altura de un rectángulo también se conocen como sus dimensiones.
En un rectángulo, cualquier lado puede elegirse como base, y el lado contiguo, como altura.
Por ejemplo, en el rectángulo ABCD, el segmento AB puede tomarse como base, y el lado contiguo BC (o AD) como altura.
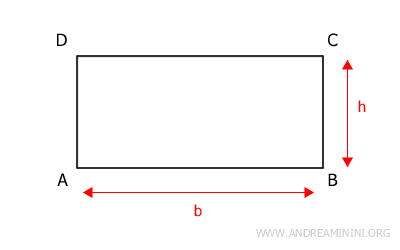
De forma equivalente, en el mismo rectángulo, se puede considerar BC como base y el lado contiguo CD (o AB) como altura.
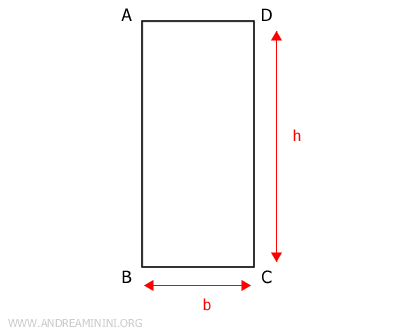
Notas adicionales
Algunas observaciones y aspectos clave sobre los rectángulos:
- Un rectángulo tiene diagonales congruentes
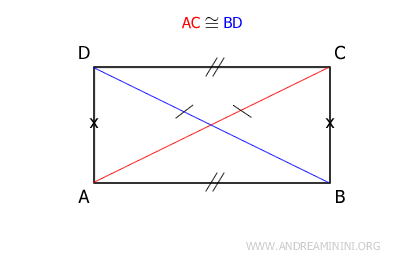
Demostración. Un rectángulo es un paralelogramo, por lo que tiene lados y ángulos opuestos congruentes (AB≅CD y AD≅BC). Además, todos sus ángulos son rectos y congruentes.
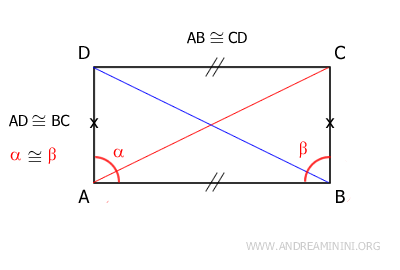
Por tanto, según el primer criterio de congruencia de triángulos, los triángulos ABD y ABC son congruentes, pues tienen lados congruentes (AB≅CD y AD≅BC) y el ángulo comprendido también es congruente (α≅β). Al ser congruentes estos dos triángulos, sus hipotenusas (AC≅BD), que son las diagonales del rectángulo, resultan congruentes. - Cada diagonal divide el rectángulo en dos triángulos rectángulos congruentes
Demostración. Un rectángulo tiene lados opuestos congruentes y ángulos rectos, lo cual basta para demostrar la congruencia de los dos triángulos que forma cualquier diagonal. Por ejemplo, la diagonal AC divide el rectángulo en los triángulos ABC y ACD.
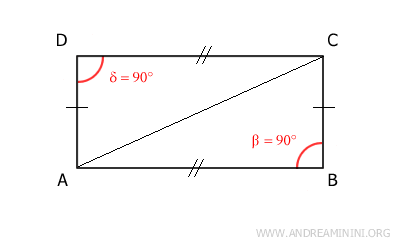
Ambos triángulos comparten el lado AC y tienen lados congruentes (AD≅BC y AB≅CD). Por tanto, según el tercer criterio de congruencia (Lado-Lado-Lado), son congruentes. Además, como tienen un ángulo recto, son también triángulos rectángulos. El mismo razonamiento se aplica a la otra diagonal, BD, del rectángulo. - Las diagonales dividen el rectángulo en cuatro triángulos isósceles, congruentes dos a dos
Demostración. Un rectángulo posee lados opuestos congruentes, diagonales congruentes y ángulos rectos. Al tratarse de un paralelogramo, sus diagonales (AC≅BD) se intersectan en su punto medio M, de modo que las mitades de las diagonales también son congruentes (AM≅CM≅BM≅DM).
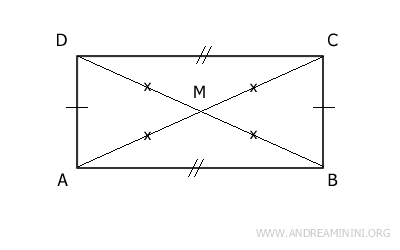
Las diagonales dividen el rectángulo en cuatro triángulos. Tomados en pares, y según el tercer criterio de congruencia (Lado-Lado-Lado), los triángulos opuestos AMD≅BMC y ABM≅CDM son congruentes, pues tienen tres lados congruentes en el mismo orden. Además, los cuatro triángulos presentan lados oblicuos congruentes, ya que coinciden con las mitades de las diagonales (AM≅CM≅BM≅DM) del rectángulo. En consecuencia, los cuatro son triángulos isósceles. - Un paralelogramo es un rectángulo si al menos uno de sus ángulos es recto
Si un ángulo de un paralelogramo es recto (90°), entonces todos los demás ángulos también lo serán. Por tanto, el paralelogramo es un rectángulo.Demostración. En un paralelogramo, los ángulos adyacentes sobre un mismo lado son ángulos suplementarios (180°). Por tanto, si uno de los ángulos mide 90° (es recto), el ángulo adyacente en ese mismo lado también ha de medir 90°, ya que los ángulos suplementarios suman 180° = 90° + 90°. Aplicando este razonamiento a cada vértice, se demuestra que todos los ángulos del rectángulo son rectos.
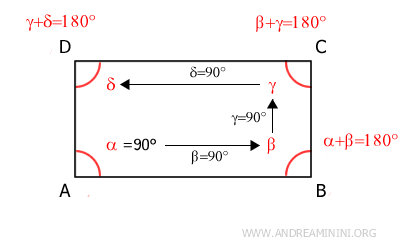
- Un paralelogramo es un rectángulo si sus diagonales son congruentes
Demostración. Si el paralelogramo ABCD tiene diagonales congruentes (AC≅BD), puede demostrarse que esta condición basta para concluir que ABCD es un rectángulo.
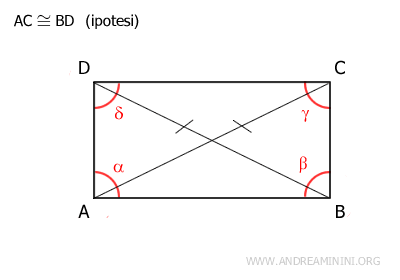
Como ABCD es un paralelogramo, presenta lados opuestos congruentes (AB≅CD y BC≅AD).
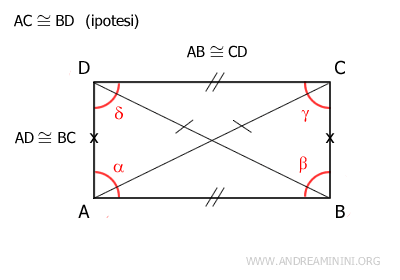
Por tanto, según el tercer criterio de congruencia, los triángulos ABC y ABD son congruentes, es decir, ABC≅ABD, ya que sus lados son congruentes en el mismo orden. En consecuencia, estos triángulos tienen también sus ángulos congruentes en el mismo orden. En particular, los ángulos α≅β son congruentes. Dado que en un paralelogramo, los ángulos adyacentes sobre un mismo lado son suplementarios α+β=180°, y siendo estos ángulos congruentes α≅β, se deduce que cada ángulo mide 90°: α=90° y β=90°. Una vez demostrado que uno de los ángulos del paralelogramo es recto, se concluye que todos los demás también lo son. Esto prueba que el paralelogramo es un rectángulo.
Y así sucesivamente...