Cálculo del Área de un Rectángulo
El área de un rectángulo se obtiene multiplicando la base por la altura: $$ A = b \ \times \ h $$ 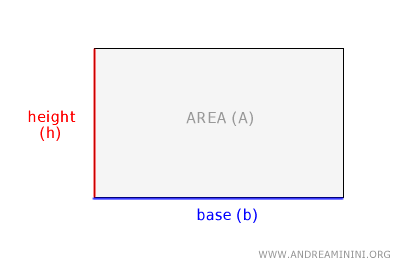
Calcular el área de un rectángulo es un procedimiento sencillo y muy intuitivo.
Para entenderlo mejor, imagina que un rectángulo es como una habitación. El área de esa habitación (o rectángulo) se determina multiplicando su largo por su ancho.
Por ejemplo, si la habitación mide 5 metros de largo y 3 metros de ancho, para hallar el área basta con multiplicar esos 5 metros (largo) por los 3 metros (ancho).
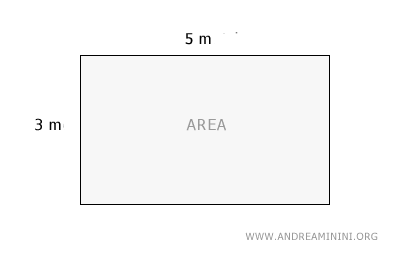
Así, el área del rectángulo es de 15 metros cuadrados. Este cálculo es muy práctico, por ejemplo, para saber cuántos metros de suelo necesitamos cubrir en toda la habitación.
$$ A = 5 \ metros \ \times \ 3 \ metros = 15 \ metros \ cuadrados \ (m^2) $$
De manera más formal, se expresa así:
$$ A = 5 \ m \times 3 \ m = 15 \ m^2 $$
En términos generales, si llamamos L al largo y W al ancho, el área A se calcula con la fórmula A = L × W.
$$ Área = Largo \ \times \ Ancho $$
Este método es sencillo y se aplica a cualquier rectángulo, sea cual sea su tamaño.
Demostración de la Fórmula
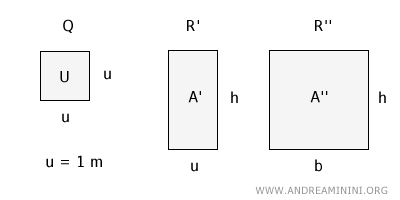
Para demostrar esta fórmula, partamos de un cuadrado Q cuyo lado mide exactamente una unidad de medida: u = 1 metro.

Este cuadrado representa 1 metro cuadrado, que es la unidad estándar para medir superficies: U = 1 m².
$$ U = 1 \ m² $$
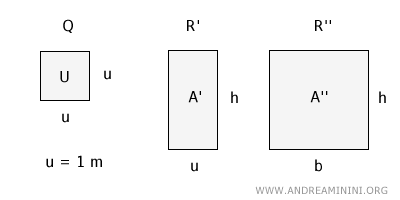
Consideremos ahora dos rectángulos: el primero, R', tiene un ancho igual a la unidad de medida (u = 1 m) y una altura h.
El segundo rectángulo, R'', tiene un ancho b (elegido libremente) y la misma altura h que el primero.
$$ A' = \frac{h \cdot m^2}{1 \ m} $$
Los rectángulos R' y R'' tienen áreas A' y A'', respectivamente, que aún no hemos calculado.
No obstante, como ambos comparten la misma altura h, la única diferencia entre ellos es su ancho. Por lo tanto, sus áreas son directamente proporcionales a sus anchos.
$$ A'' : A' = b : u $$
Sabemos que el ancho del rectángulo R' es la unidad de medida, es decir, u = 1 m.
$$ A'' : A' = b : 1 \ m $$
Aplicando las propiedades de las proporciones, se deduce que el área A'' del rectángulo R'' es igual al producto del área A' del rectángulo R' por la base b.
$$ A'' = b \cdot A' \cdot m $$
Aún nos falta determinar el valor de A', el área del rectángulo R'.
Para resolverlo, comparemos el rectángulo R' con el cuadrado Q.
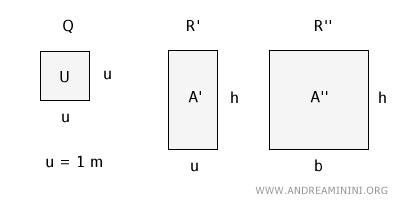
El rectángulo R' y el cuadrado Q tienen la misma base (u = 1 m), por lo que sus áreas son proporcionales a sus alturas.
$$ A' : U = h : u $$
Como sabemos que U = 1 m² y u = 1 m:
$$ A' : 1 \ m² = h : 1 \ m $$
Usando las propiedades de las proporciones, tenemos:
$$ \frac{A'}{1 \ m²} = \frac{h}{1 \ m} $$
Multiplicando ambos lados por 1 m², obtenemos:
$$ \frac{A'}{1 \ m²} \cdot m² = \frac{h}{1 \ m} \cdot m² $$
$$ A' = h \cdot m $$
Así, concluimos que A' = h metros.
$$ A' = h \cdot m $$
Una vez conocida el área del rectángulo R', que es A' = h·m, podemos sustituirla en la proporción anterior.
$$ A'' = b \cdot A' \cdot m $$
$$ A'' = b \cdot ( h \cdot m ) \cdot m $$
$$ A'' = b \cdot h \ \cdot m^2 $$
Es decir:
$$ A'' = b \cdot h \ m² $$
Esto demuestra que el área del rectángulo R'' es igual al producto de su base (b) por su altura (h), y se mide en metros cuadrados.
Y así sucesivamente.