Polígonos circunscritos a una circunferencia
Un polígono se dice circunscrito a una circunferencia cuando todos sus lados son tangentes a la circunferencia en puntos de contacto.
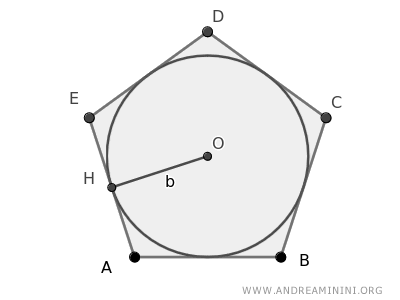
Esto equivale a decir que la circunferencia está inscrita en el polígono.
El centro de dicha circunferencia se denomina incentro, y su radio recibe el nombre de inradio.
A esta circunferencia se la llama incírculo.
No todos los polígonos pueden circunscribirse a una circunferencia. Por ejemplo, todos los triángulos pueden ser circunscritos. Sin embargo, un cuadrilátero solo puede serlo si la suma de las longitudes de sus lados opuestos es igual. En cambio, todos los polígonos regulares - pentágonos, hexágonos, etc. - son siempre circunscritos, ya que por definición cada lado es tangente a una circunferencia común.
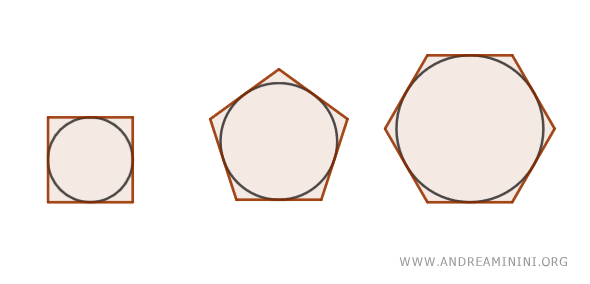
Área de los polígonos circunscritos
El área de un polígono regular circunscrito a una circunferencia se obtiene multiplicando el semiperímetro (p) por el radio (r) de la circunferencia: $$ A = p \cdot r $$
Esta fórmula se basa en que un polígono circunscrito puede considerarse equivalente a un triángulo cuya base es el perímetro (P) del polígono y cuya altura es el radio (r) de la circunferencia.
Dado que el área de un triángulo es la mitad del producto de su base por su altura, se deduce directamente la fórmula para el área del polígono circunscrito:
$$ A = \frac{P \cdot r}{2} = \frac{P}{2} \cdot r = p \cdot r $$
Siendo P el perímetro y p el semiperímetro (P = 2p).
Además, como en los polígonos regulares el radio (r) coincide con el apotema (a), el área puede calcularse también como:
$$ A = p \cdot a $$
Ejemplo
Consideremos este pentágono regular circunscrito, cuya área conocida es A = 15.48:
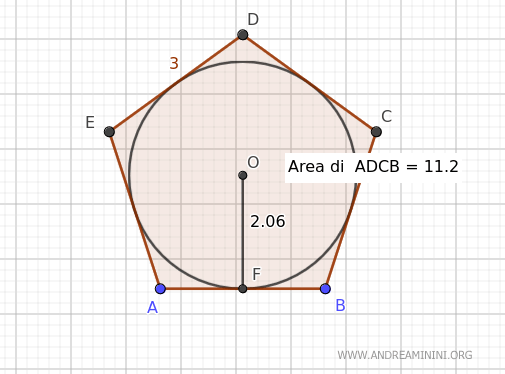
La longitud de cada lado es 3 unidades, y el radio del incírculo es r = 2.06.
El semiperímetro es:
$$ p = \frac{3 \cdot 5}{2} = \frac{15}{2} = 7.5 $$
Multiplicando por el radio:
$$ A = p \cdot r = 7.5 \cdot 2.06 = 15.48 $$
Si descomponemos el pentágono en cinco triángulos, el área de cada triángulo es: base (lado del pentágono) por altura (radio) dividido por dos:
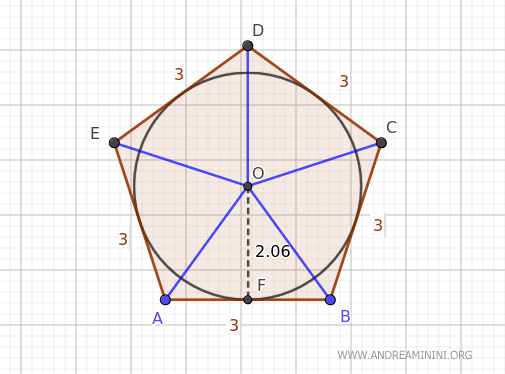
La suma de sus áreas nos da el área total del pentágono:
$$ A = 5 \cdot \frac{3 \cdot 2.06}{2} = \frac{5 \cdot 3}{2} \cdot 2.06 $$
El resultado coincide:
$$ A \cong 15.48 $$
Este método es aplicable a cualquier polígono regular, ya que todos pueden circunscribirse a una circunferencia.
Teorema del polígono circunscrito
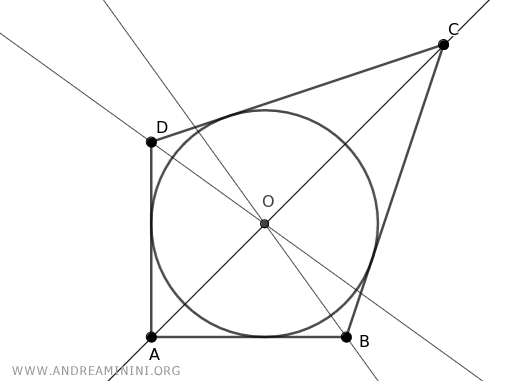
Un polígono convexo solo puede circunscribirse a una circunferencia si las bisectrices de todos sus ángulos se cortan en un único punto (el incentro).
Si las bisectrices no concurren en un mismo punto, el polígono no puede ser circunscrito.
El recíproco también es cierto: si un polígono convexo es circunscrito, entonces las bisectrices de sus ángulos se cortan en un único punto: el incentro.
En los triángulos y en los polígonos regulares siempre existe un incentro en el que confluyen las bisectrices. Solo ciertos polígonos irregulares que sean circunscritos comparten esta propiedad.
Ejemplo práctico
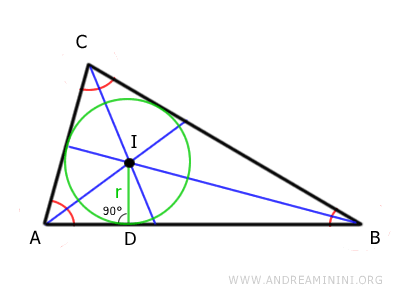
Por ejemplo, en todo triángulo las bisectrices de sus ángulos se cortan siempre en un punto: el incentro.
Si se traza una circunferencia con centro en este punto (I) y radio adecuado (r), esta será tangente a todos los lados del triángulo:
Demostración del teorema
Para demostrar el teorema, consideremos un polígono cuyas bisectrices se cortan en un único punto O:
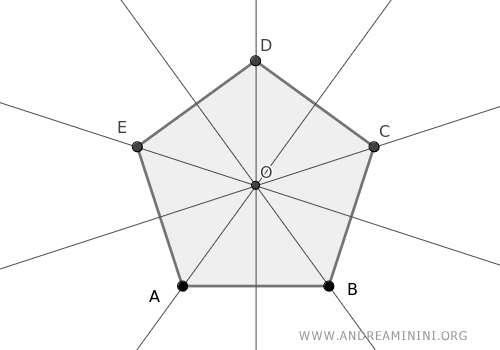
La bisectriz de un ángulo es la recta que divide el ángulo en dos partes iguales.
Queremos demostrar que puede trazarse una circunferencia tangente a todos los lados.
Por definición, la bisectriz es el lugar geométrico de los puntos equidistantes de los lados del ángulo:
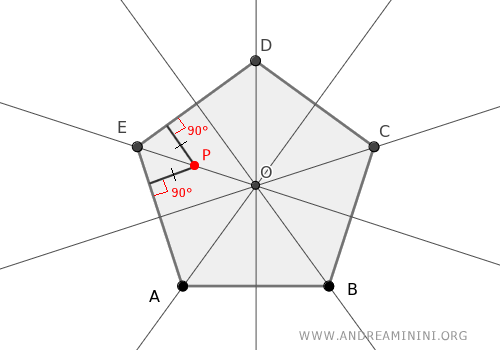
Así, el punto O es equidistante de todos los lados del polígono:
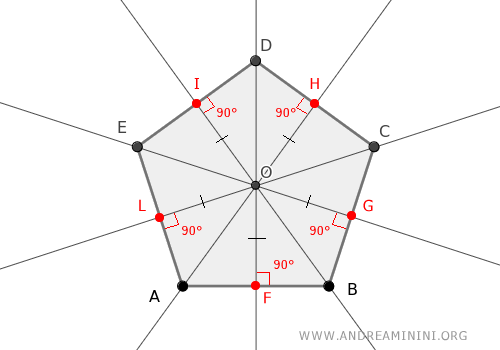
Por tanto, puede trazarse una circunferencia de centro O y radio d, tangente a todos los lados:
$$ \text{incírculo} $$
Así demostramos que el polígono es circunscrito a una circunferencia:
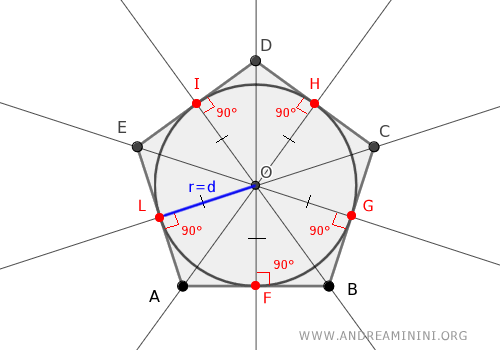
El teorema queda demostrado.