Única Circunferencia que Pasa por Tres Puntos No Colineales
Por tres puntos no colineales en el plano puede trazarse una única circunferencia.
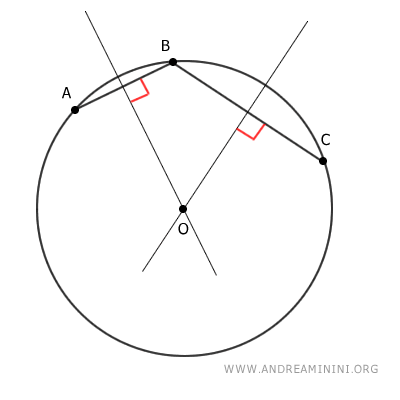
Este teorema demuestra tanto la existencia como la unicidad de una circunferencia que pase por tres puntos no colineales.
Un Ejemplo Práctico
Comenzamos situando tres puntos no colineales en el plano.
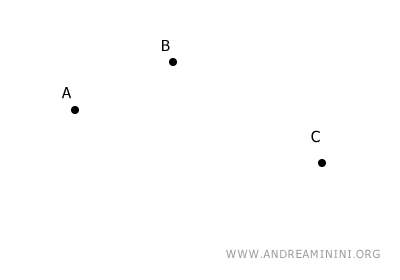
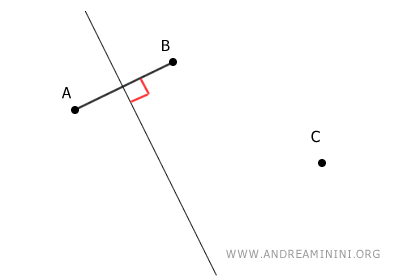
Unimos los puntos A y B para formar el segmento AB.
Después, hallamos el punto medio M de AB y trazamos la mediatriz del segmento pasando por M.
A continuación, unimos los puntos B y C para formar el segmento BC.
De manera análoga, localizamos el punto medio de BC y trazamos su mediatriz.
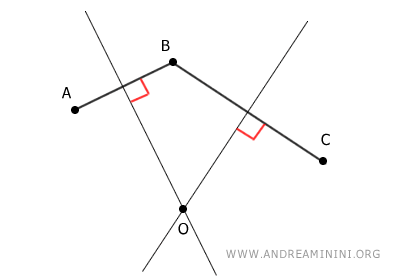
Las mediatrices de los segmentos AB y BC se cortan en el punto O, que es equidistante de los puntos A, B y C.
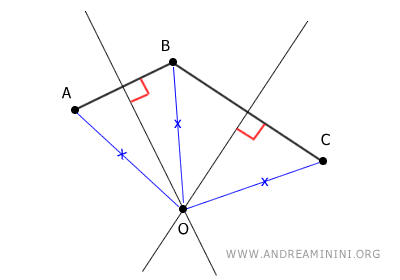
Explicación: Las mediatrices de un segmento reúnen todos los puntos situados a igual distancia de los extremos del segmento. Por eso, el punto O, ubicado en la intersección de las mediatrices de AB y BC, es equidistante de A, B y C.
Luego, trazamos una circunferencia con centro en O y radio igual a OA (también podría ser OB o OC, ya que sus longitudes coinciden).
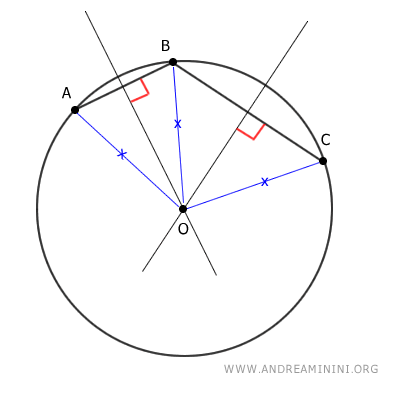
Obtenemos así una circunferencia que pasa exactamente por los puntos A, B y C, lo que confirma el teorema.
No solo existencia, sino unicidad: Este teorema no solo asegura que existe una circunferencia que pase por A, B y C, sino que además prueba que ninguna otra distinta puede cumplir esta condición. La intersección de las mediatrices determina de manera única el punto O, lo que excluye la posibilidad de otro centro que equidiste de los tres puntos. Más detalles se abordan en la demostración.
Demostración
El teorema afirma la existencia y unicidad de una circunferencia que pase por tres puntos no alineados A, B y C en el plano.
Existencia
El punto O se encuentra sobre las mediatrices de los segmentos AB y BC.
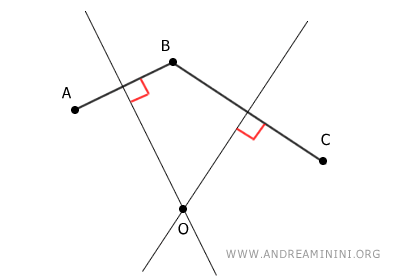
Como lugar geométrico, la mediatriz de un segmento contiene todos los puntos que se hallan a la misma distancia de sus extremos. Esto implica que los segmentos OA y OB son congruentes, y del mismo modo, OB y OC.
$$ \overline{OA} \cong \overline{OB} $$
$$ \overline{OB} \cong \overline{OC} $$
Por transitividad, si OA = OB y OB = OC, entonces OA = OC.
$$ \overline{OA} \cong \overline{OC} $$
En consecuencia, el punto O se encuentra a igual distancia de A, B y C.
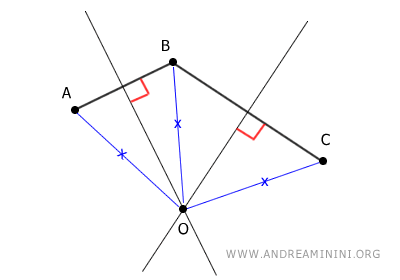
Esto significa que los puntos A, B y C pertenecen a la circunferencia centrada en O.
Unicidad
Como A, B y C no están alineados, los segmentos AB y BC no son paralelos y, por lo tanto, se cruzan.
Las rectas que contienen a los segmentos AB y BC son secantes y se intersectan en un único punto, que es el punto B.
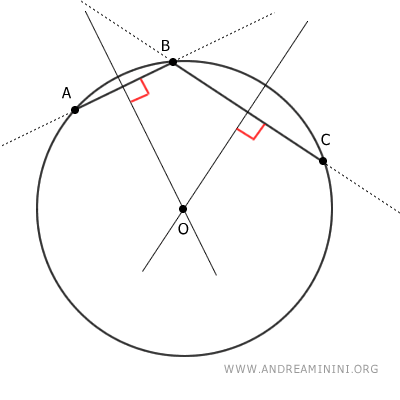
Las perpendiculares a dos rectas secantes también se cortan, lo que asegura que las mediatrices de los segmentos AB y BC se intersectan en un único punto.
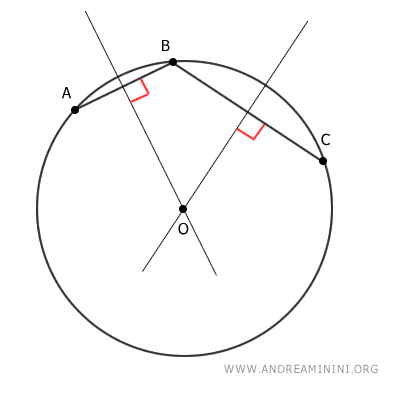
Por lo tanto, el punto O es el único que equidista de A, B y C. No puede existir otro punto que cumpla esta condición.
Conclusión
En definitiva, existe una única circunferencia que pasa por los tres puntos A, B y C, tal como afirma este teorema.
Y con esto concluye la explicación.