Recta Polar y Tangentes

La recta polar de las tangentes es una línea, r, asociada a un punto P exterior a una cónica (por ejemplo, una circunferencia). Los puntos de contacto A y B entre r y la cónica coinciden con los puntos de tangencia de las tangentes a la cónica que pasan por P.

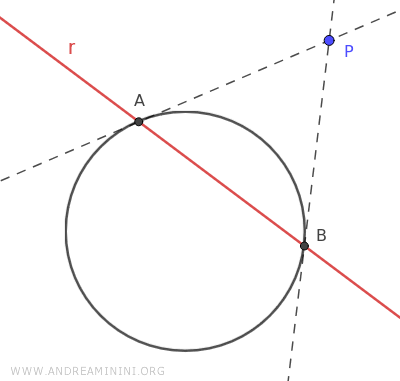
Para comprender mejor este concepto, consideremos una circunferencia \(\mathcal{C}\) y un punto \(P\) situado en su exterior.

Se trazan las tangentes a la circunferencia que pasan por el punto exterior P.

Como P está fuera de la circunferencia, existen dos tangentes, y por lo tanto, dos puntos de tangencia con la circunferencia.

La recta polar asociada a P es la línea (de color rojo) que pasa por los dos puntos de tangencia, A y B, en la circunferencia.

Para hallar la ecuación de la recta polar de una cónica \( Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 \) respecto a un punto \( P(x_0, y_0) \), se emplea la siguiente fórmula:

$$ Axx_0 + B\left(\frac{xy_0 + yx_0}{2}\right) + Cyy_0 + Dx + Ey + F = 0 $$

Nota: La recta polar de las tangentes establece un vínculo entre una cónica y cualquier punto exterior, pues define el lugar geométrico de las tangentes a la cónica que pasan por ese punto.

Ejemplo Práctico

Como ejemplo, consideremos una circunferencia y un punto \( Q(6, 8) \) situado en su exterior:

$$ x^2 + y^2 - 25 = 0 $$

$$ Q(6,8) $$

Utilizamos la fórmula:

$$ Axx_0 + B\left(\frac{xy_0 + yx_0}{2}\right) + Cyy_0 + Dx + Ey + F = 0 $$

Sustituyamos los coeficientes de la cónica: A=1, B=0, C=1, D=0, E=0, F=-25

$$ 1 \cdot xx_0 + 0 \cdot \left(\frac{xy_0 + yx_0}{2}\right) + 1 \cdot yy_0 + 0 \cdot x + 0 \cdot y - 25 = 0 $$

$$ xx_0 + yy_0 - 25 = 0 $$

Explicación: Una cónica se representa en general mediante la ecuación $$ Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 $$. En este caso, se trata de la circunferencia $$ x^2 + y^2 = 25 $$, cuyos coeficientes son A=1, B=0, C=1, D=0, E=0, F=-25.

Las coordenadas del punto exterior Q(6,8) son x₀=6 y y₀=8.

$$ x \cdot 6 + y \cdot 8 - 25 = 0 $$

Así, obtenemos la ecuación de la recta polar:

$$ 6x + 8y - 25 = 0 $$

Esta recta representa la polar del punto \( Q(6, 8) \) con respecto a la circunferencia \( x^2 + y^2 = 25 \).

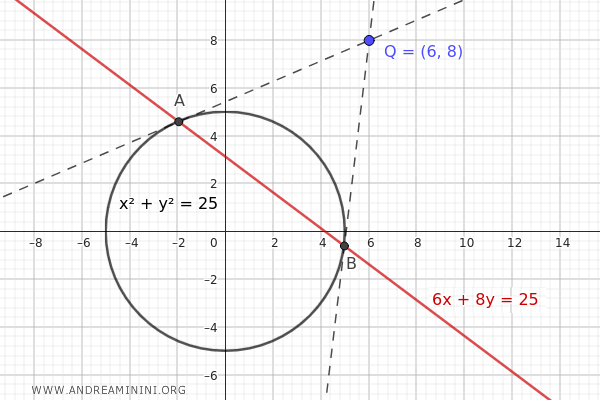
Como se observa en el gráfico, los dos puntos de intersección A y B entre la recta polar y la circunferencia coinciden con los puntos de tangencia de las dos tangentes que pasan por el punto exterior \( Q(6, 8) \).

Observaciones

Algunas observaciones útiles sobre la recta polar:

• Si el punto P está sobre la circunferencia, la recta polar coincide con la tangente en P
  Cuando un punto P pertenece a una cónica, como una circunferencia, su recta polar coincide exactamente con la recta tangente a la cónica en ese punto.

  Ejemplo: Consideremos una circunferencia centrada en el origen y de radio \( r=5 \). $$ x^2 + y^2 = 25 $$ Tomemos ahora el punto \(P(3, 4)\), que pertenece a la circunferencia. Aplicamos la fórmula: $$ Axx_0 + B\left(\frac{xy_0 + yx_0}{2}\right) + Cyy_0 + Dx + Ey + F = 0 $$ En este caso, los coeficientes son A=1, B=0, C=1, D=0, E=0, F=-25 $$ xx_0 + yy_0 - 25 = 0 $$ Las coordenadas del punto P(3,4) son x₀=3 y y₀=4. $$ 3x + 4y - 25 = 0 $$ Esta ecuación representa la recta tangente a la circunferencia en el punto P(3,4).
  

• Si el punto P está dentro de la circunferencia, no existe tangente real ni secante
  Si el punto P se encuentra en el interior de la circunferencia, la ecuación de la recta asociada a ese punto resulta exterior a la circunferencia. En consecuencia, no existe ninguna tangente real ni secante que pase por P. No obstante, el concepto de recta polar sigue siendo válido desde el punto de vista geométrico, aunque en este caso no represente una tangente real.

  Ejemplo: Consideremos la misma circunferencia del ejemplo anterior: $$ x^2 + y^2 = 25 $$ y el punto interior \( P(2, 1) \). Aplicamos nuevamente la fórmula: $$ Axx_0 + B\left(\frac{xy_0 + yx_0}{2}\right) + Cyy_0 + Dx + Ey + F = 0 $$ En este caso, los coeficientes son A=1, B=0, C=1, D=0, E=0, F=-25 $$ xx_0 + yy_0 - 25 = 0 $$ Las coordenadas del punto P(2,1) son x₀=2 y y₀=1. $$ 2x + y - 25 = 0 $$ Esta ecuación representa una recta exterior a la circunferencia, por lo que no es ni una tangente real ni corta a la circunferencia en ningún punto.
  

Y así sucesivamente.