Circunferencia
La circunferencia es el perímetro de un círculo, una figura geométrica bidimensional formada por todos los puntos de un plano que se encuentran a la misma distancia constante (conocida como radio “r”) de un punto fijo O, llamado centro.
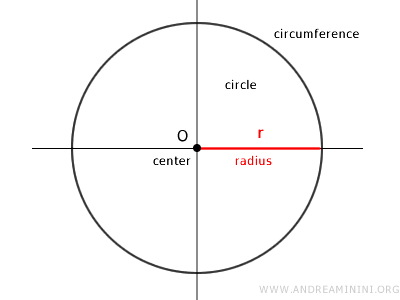
La circunferencia está compuesta por todos los puntos que se hallan a la misma distancia del centro.
La distancia entre cualquier punto de la circunferencia y el centro (O) recibe el nombre de radio.
En otras palabras, la circunferencia es el perímetro o borde de un círculo, mientras que el círculo corresponde a la superficie encerrada dentro de esa circunferencia.

El círculo también puede definirse como el conjunto de puntos cuya distancia al centro es menor o igual al radio. ¿Cuál es la diferencia entre circunferencia y círculo? La circunferencia es la línea que delimita la figura plana, mientras que el círculo es toda la región comprendida en su interior. Es decir, la circunferencia constituye el contorno o perímetro del círculo, y el círculo incluye tanto esa línea como la superficie que encierra.
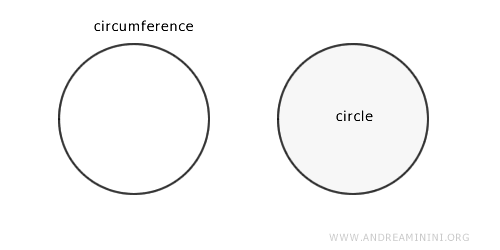
Así, el círculo es la figura plana que abarca tanto los puntos de la circunferencia como todos los puntos situados en su interior.
La longitud de la circunferencia (C) se calcula mediante la fórmula 2πr
$$ C = 2 \pi r $$
donde r representa el radio y π (pi) es una constante matemática cuyo valor aproximado es 3,14.
Dado que el diámetro (d) equivale al doble del radio, es decir, d = 2r, también puede expresarse así:
$$ C = \pi \cdot d $$
¿Qué es pi? La razón entre la longitud de una circunferencia y su diámetro es un valor constante, representado con el símbolo π, conocido como pi, cuyo valor aproximado es 3,14. $$ π=3.14159 $$
Fórmulas de la Circunferencia
Las fórmulas fundamentales para calcular las dimensiones de la circunferencia son:
- Longitud de la circunferencia
La longitud de una circunferencia (o su perímetro) se obtiene con la fórmula 2πr, donde π es la constante matemática “pi”, cuyo valor aproximado es 3,14159, y “r” corresponde al radio. $$ C = 2 \cdot \pi \cdot r $$ - Área
El área del círculo delimitado por la circunferencia se calcula mediante la fórmula: $$ A = \pi \cdot r^2 $$ - Radio
El radio se obtiene dividiendo la longitud de la circunferencia entre 2π: $$ r = \frac{C}{2\pi} $$ - Diámetro
El diámetro es la distancia que separa dos puntos opuestos de la circunferencia, pasando por el centro. Es exactamente el doble del radio. $$ d = 2r $$
El Radio
El radio de una circunferencia es un segmento que une el centro O de la circunferencia con cualquier punto P ubicado sobre ella.
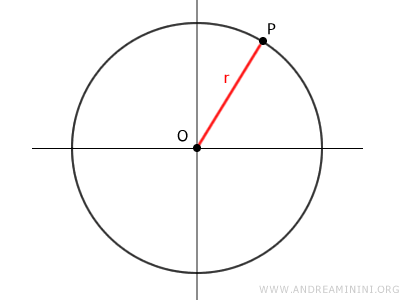
Por tanto, existen infinitos segmentos que representan el radio, y todos son congruentes, ya que poseen la misma longitud.
La fórmula para calcular el radio es la siguiente:
$$ r = \frac{C}{2 \pi} $$
Sabemos que la longitud de la circunferencia equivale al doble del producto del radio por pi: $$ C = 2 \pi r $$ Si dividimos ambos miembros de la ecuación entre 2π, obtenemos la fórmula del radio: $$ \frac{C}{2 \pi} = \frac{2 \pi r}{2 \pi} $$ $$ \frac{C}{2 \pi} = r $$
Los Arcos
Cualquier par de puntos A y B sobre una circunferencia la divide en dos partes, denominadas arcos.
Un arco es un tramo curvo de la circunferencia comprendido entre los puntos A y B.
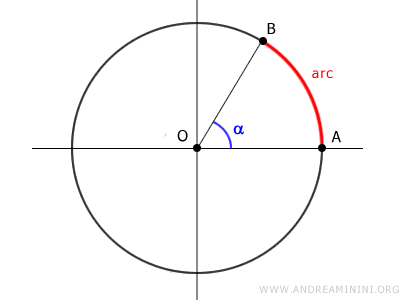
La longitud del arco puede determinarse teniendo en cuenta la amplitud del ángulo α:
$$ l_a = 2 \pi r \cdot \frac{ \alpha }{360°} $$
donde 2πr representa la longitud total de la circunferencia.
Existe, por tanto, una relación directa entre la longitud del arco, la amplitud del ángulo y el radio de la circunferencia.
Ejemplo. Si una circunferencia tiene un radio de 10 cm y la amplitud del ángulo es de 90°, la longitud del arco se calcula así: $$ l_a = 2 \pi \cdot 10 \cdot \frac{ 90 }{360} = 2 \pi \cdot 10 \cdot \frac{1}{4} = 5 \pi $$
Cuerdas
Una cuerda de una circunferencia es cualquier segmento cuyos extremos se encuentran en dos puntos distintos A y B de la misma.
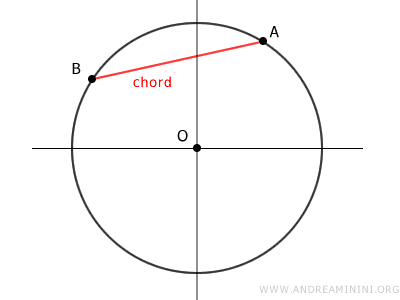
Si la cuerda, además, pasa por el centro, se le denomina diámetro de la circunferencia.
El Diámetro
El diámetro es un segmento que une dos puntos distintos sobre la circunferencia y que pasa por su centro.
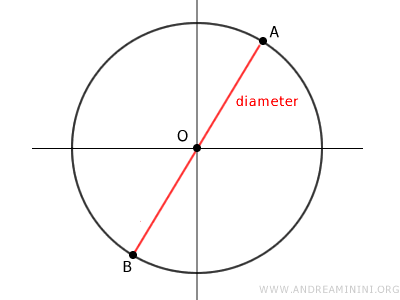
En esencia, el diámetro es una cuerda especial que atraviesa el centro de la circunferencia. Es, además, la cuerda más larga que puede trazarse en ella.
La longitud del diámetro equivale a 2r, es decir, el doble del radio.
$$ d = 2r $$
Existen infinitos segmentos que pueden funcionar como diámetros de una circunferencia, todos ellos congruentes entre sí porque poseen la misma longitud.
Postulado de la Circunferencia
Dado un punto O y cualquier segmento AB en un plano, existe una única circunferencia cuyo centro se sitúa en el punto O y cuyo radio es igual a la longitud del segmento AB.
La Ecuación de la Circunferencia
La ecuación en forma estándar de la circunferencia en el plano cartesiano se expresa así:
$$ (x - x_0)^2 + (y - y_0)^2 = r^2 $$
Donde (x0, y0) son las coordenadas del centro O de la circunferencia y r es su radio.
De manera equivalente, la ecuación general de la circunferencia puede escribirse de la siguiente forma:
$$ x^2 + y^2 + ax + by + c = 0 $$
Siendo sus parámetros: a = -2x0, b = -2y0 y c = x02 + y02 - r2.
En este contexto, las coordenadas (x0, y0) del centro de la circunferencia son:
$$ (x_0 ; y_0) = \left( - \frac{a}{2} ; - \frac{b}{2} \right) $$
Mientras que el radio se obtiene mediante la siguiente expresión:
$$ r = \sqrt{ \left( - \frac{a}{2} \right)^2 + \left( - \frac{b}{2} \right)^2 - c } $$
La ecuación de la circunferencia también puede expresarse de forma explícita, de este modo: $$ y = y_0 \pm \sqrt{r^2 - (x - x_0)^2 } $$
Es fundamental tener en cuenta que la ecuación x2 + y2 + ax + by + c = 0 no siempre representa una circunferencia real.
Representa efectivamente una circunferencia con centro en C solo si se cumple esta condición de existencia real:
$$ \left( -\frac{a}{2} \right)^2 + \left( -\frac{b}{2} \right)^2 - c \ge 0 $$
Esto se debe a que el radio (r) es una distancia entre dos puntos - una magnitud que, como longitud, debe ser siempre un número no negativo (r ≥ 0).

En otras palabras, esta ecuación es una condición necesaria, pero no suficiente, para garantizar la existencia de una circunferencia real.
En el caso particular en que el radio sea cero (r=0), la circunferencia se denomina circunferencia degenerada.
Nota. Si el resultado bajo la raíz cuadrada fuese negativo, se obtendría un número imaginario, lo cual impediría resolver la ecuación en el campo de los números reales. $$ r = \sqrt{\left( -\frac{a}{2} \right)^2 + \left( -\frac{b}{2} \right)^2 - c} $$
Ejemplo
Deseo trazar una circunferencia con centro en el punto (x; y) = (1; 3) y radio r = 2.
En este caso, x0 = 1 y y0 = 3.
$$ (x - x_0)^2 + (y - y_0)^2 = r^2 $$
$$ (x - 1)^2 + (y - 3)^2 = r^2 $$
El radio de la circunferencia es r = 2.
$$ (x - 1)^2 + (y - 3)^2 = 2^2 $$
$$ (x - 1)^2 + (y - 3)^2 = 4 $$
Esta ecuación se cumple para todos los puntos situados a una distancia de 2 unidades del punto (1; 3) en el plano.
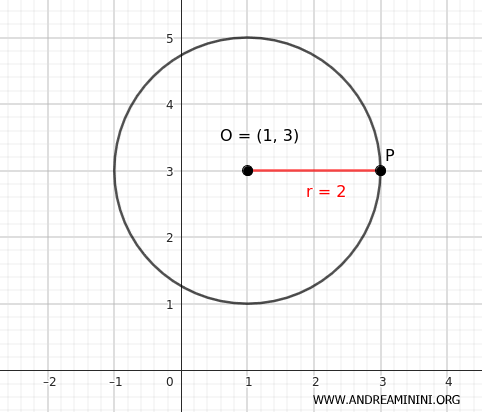
Así, he logrado trazar la circunferencia que pretendía construir.
Observaciones
Algunas consideraciones acerca de las circunferencias:
- Una circunferencia es simétrica respecto de su centro y de cualquier recta que pase por él.
- La circunferencia es convexa, ya que cualquier par de puntos situados sobre ella pueden unirse mediante un segmento que permanece completamente en su interior.
- Principios de congruencia en una circunferencia
En una circunferencia, si dos cuerdas, dos arcos, dos sectores circulares, dos segmentos circulares o dos ángulos centrales son congruentes, entonces las demás magnitudes asociadas también lo serán. Esto ocurre porque todas estas dimensiones están vinculadas de manera biunívoca. Por ejemplo, a un ángulo central le corresponde un arco determinado, y viceversa.
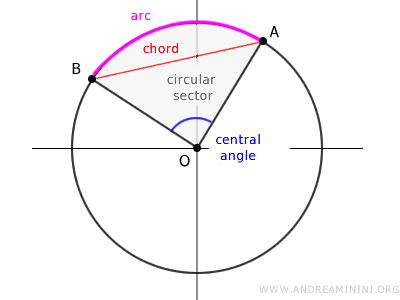
- Los círculos: integrantes de la familia de las secciones cónicas
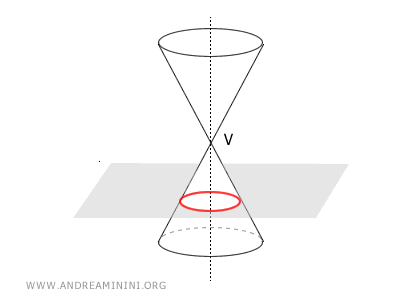
Los círculos forman parte de la familia de las secciones cónicas, ya que se generan al cortar un cono con un plano perpendicular a su eje. Esta intersección da lugar a un círculo sobre la superficie del cono.
Y así sucesivamente.