Teorema del Ángulo Inscrito
En cualquier circunferencia, la medida de un ángulo inscrito es siempre la mitad de la medida del arco que subtiende.
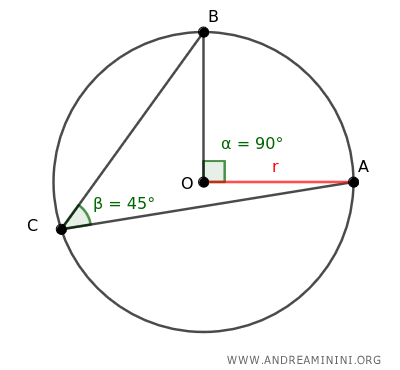
Dicho de forma sencilla, si se tiene un ángulo inscrito que subtiende un arco de α grados, entonces su medida será de α/2 grados.
Este principio se cumple para cualquier arco y ángulo inscrito en una circunferencia, no solo en el caso de las semicircunferencias.
Un Ejemplo Práctico
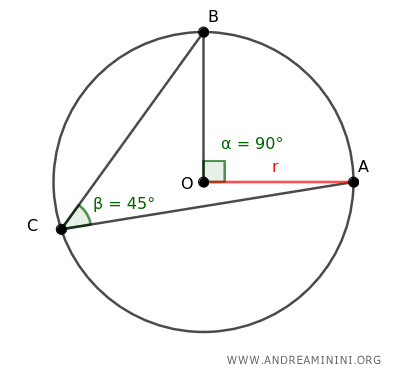
Imaginemos una circunferencia con centro O y radio r.
Consideremos tres puntos distintos A, B y C sobre la circunferencia.
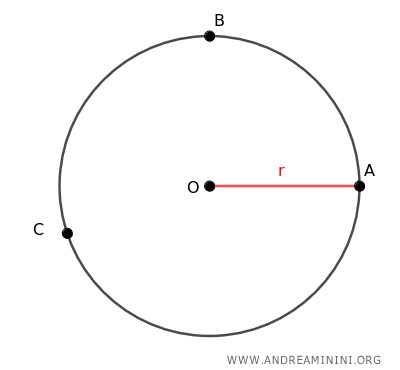
Unimos los puntos B y C, y también A y C, formando así el ángulo inscrito ∠ACB dentro de la circunferencia.
En este caso, el ángulo ACB mide 45°.
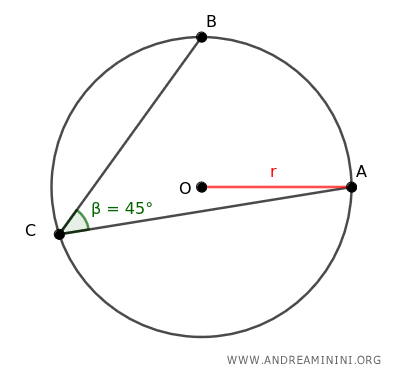
De acuerdo con el Teorema del Ángulo Inscrito, la medida de un ángulo inscrito es siempre la mitad de la del arco que subtiende.
En este ejemplo, el arco en cuestión es el segmento AB de la circunferencia.
Si trazamos los segmentos OA y OB, definimos el ángulo central ∠AOB, que subtiende el arco AB.
El ángulo central ∠AOB mide 90°, es decir, el doble que el ángulo inscrito (45°).
La Demostración
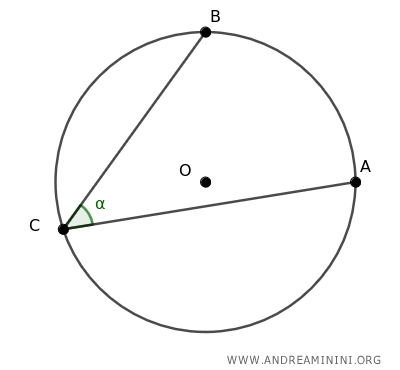
Consideremos una circunferencia con centro O y tres puntos A, B y C sobre su perímetro.
Los puntos A y B forman el ángulo inscrito ∠ACB.
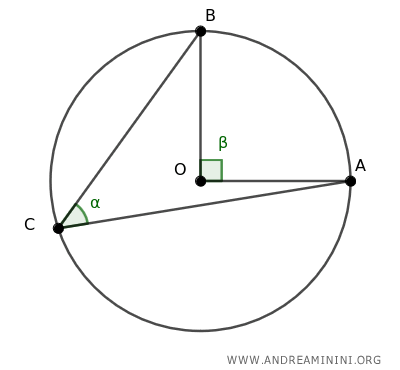
A continuación, trazamos los segmentos OA y OB.
El ángulo central ∠AOB abarca el arco AB.
También trazamos el segmento OC.
Los triángulos OAC y OBC son ambos isósceles, ya que OA y OC son radios de la misma circunferencia, al igual que OB y OC.
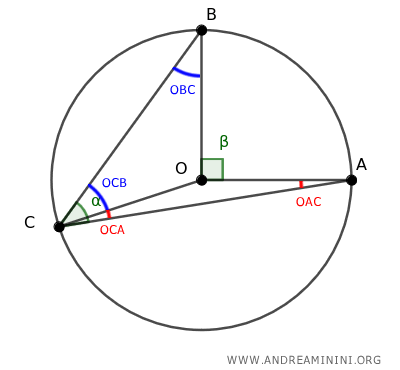
Dado que en un triángulo isósceles los ángulos en la base son congruentes, se deduce que ∠OCA ≡ ∠OAC y ∠OCB ≡ ∠OBC.
El ángulo inscrito ∠ACB es la suma de los ángulos ∠OCA y ∠OCB.
$$ ∠ACB = ∠OCA + ∠OCB $$
Si prolongamos el segmento OC hasta el punto D, obtenemos el diámetro CD de la circunferencia.
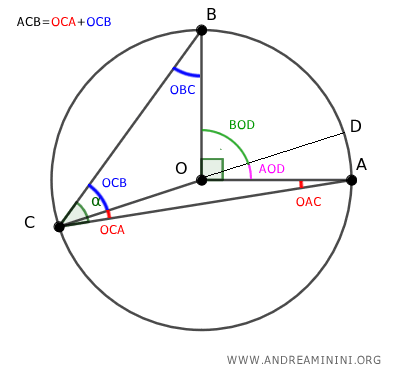
El ángulo ∠AOD es un ángulo exterior del triángulo OAC. Según el Teorema del Ángulo Exterior, equivale a la suma de los ángulos internos no adyacentes ∠OCA y ∠OAC.
$$ ∠AOD = ∠OCA + ∠OAC $$
Como ∠OCA es congruente con ∠OAC, podemos simplificar a ∠AOD = 2 × ∠OCA.
$$ ∠AOD = 2 × ∠OCA $$
De manera análoga, el ángulo ∠BOD es exterior al triángulo OBC. Por el mismo Teorema del Ángulo Exterior, equivale a la suma de los ángulos internos no adyacentes ∠OBC y ∠OCB.
$$ ∠BOD = ∠OBC + ∠OCB $$
Dado que ∠OBC es congruente con ∠OCB, se concluye que ∠BOD = 2 × ∠OCB.
$$ ∠BOD = 2 × ∠OCB $$
Como el ángulo ∠AOB es la suma de los ángulos ∠AOD y ∠BOD, se cumple:
$$ ∠AOB = ∠AOD + ∠BOD $$
Y dado que ∠AOD = 2 × ∠OCA y ∠BOD = 2 × ∠OCB, se obtiene:
$$ ∠AOB = 2 × ∠OCA + 2 × ∠OCB $$
$$ ∠AOB = 2 × ( ∠OCA + ∠OCB ) $$
Reconociendo que ∠OCA + ∠OCB corresponde a ∠ACB, podemos afirmar:
$$ ∠AOB = 2 × ∠ACB $$
Esto demuestra, de manera elegante, que el ángulo inscrito ∠ACB mide exactamente la mitad del ángulo central ∠AOB que subtiende el mismo arco.
$$ \frac{ ∠AOB }{2} = ∠ACB $$
Y con esto queda concluida la demostración.